高考数学普通高等学校招生全国统一考试83
第Ⅰ卷 (选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数![]() 的最小正周期是(
)
的最小正周期是(
)
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
解:T=![]() =π,选(B)
=π,选(B)
2.设全集![]() ,则
,则![]() =( )
=( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
解:![]() ={1,2,},故
={1,2,},故![]() ={1,2},选(A)
={1,2},选(A)
3.点![]() 到直线
到直线![]() 的距离是( )
的距离是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:点![]() 到直线
到直线![]() 的距离d=
的距离d=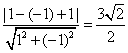 ,选(D)
,选(D)
4.设![]() ,则
,则![]() =( )
=( )
(A) ![]() (B)0 (C)
(B)0 (C)![]() (D)
1
(D)
1
解:![]() =
=![]() =0,
=0, ![]() =f(0)=1,选(D)
=f(0)=1,选(D)
5.在![]() 的展开式中,含
的展开式中,含![]() 的项的系数是(
)
的项的系数是(
)
(A)![]() (B) 5 (C)
(B) 5 (C) ![]() (D)
10
(D)
10
解:![]() 中x3的系数为10,
中x3的系数为10,![]() 中x3的系数为-20,∴
中x3的系数为-20,∴![]() 的展开式中x3的系数为-10,选(C)
的展开式中x3的系数为-10,选(C)
6.从存放号码分别为1,2,…,10的卡片的盒子中,在放回地取100次,每次取一张卡片并记下号码,统计结果如下:
| 卡片号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 取到的次数 | 13 | 8 | 5 | 7 | 6 | 13 | 18 | 10 | 11 | 9 |
则取到号码为奇数的频率是( )
(A)0.53 (B) 0.5 (C) 0.47 (D) 0.37
解:取到号码为奇数的频率是![]() =0.53,选(A)
=0.53,选(A)
7.设![]() 为两个不同的平面,
为两个不同的平面,![]() 为两条不同的直线,且
为两条不同的直线,且![]() ,有如下的两个命题:
,有如下的两个命题:
①若![]() ∥
∥![]() ,则l∥m;②若l⊥m,则
,则l∥m;②若l⊥m,则![]() ⊥
⊥![]() .
.
那么
(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题
(C) ①②都是真命题 (D) ①②都是假命题
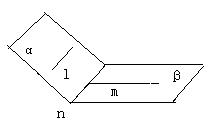 解:命题②有反例,如
解:命题②有反例,如
图中平面α∩平面β=直线n,l![]()
且l∥n,m⊥n,则m⊥l,显然平面α不垂直平面β
故②是假命题;命题①显然也是假命题,
因此本题选(D)
8.已知向量![]() ,且
,且![]() ,则由x的值构成的集合是( )
,则由x的值构成的集合是( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
解:由![]() 得
得![]() =0,即(x-5)·2+3×x=0解得x=2,选(C)
=0,即(x-5)·2+3×x=0解得x=2,选(C)
9.函数![]() 的图象与直线
的图象与直线![]() 相切,则
相切,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)1
(D)1
解:由题意,得![]() 有两个等实根,得a=
有两个等实根,得a=![]() ,选(B)
,选(B)
10.设集合![]() ,则A所表示的平面区域(不含边界的阴影部分)是( )
,则A所表示的平面区域(不含边界的阴影部分)是( )
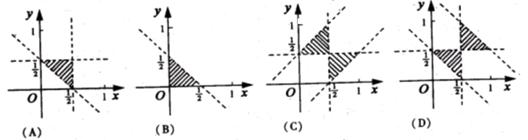
解:由题意可知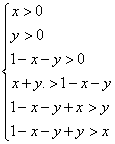 得
得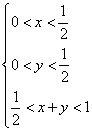 由此可知A所表示的平面区域(不含边界的阴影部分)是(A )
由此可知A所表示的平面区域(不含边界的阴影部分)是(A )
第Ⅱ卷 (非选择题 共100分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在答题卡的相应位置。
11.函数![]() 的反函数是_________.
的反函数是_________.
解:由y=![]() (x∈R,且x≠-2),得x=
(x∈R,且x≠-2),得x=![]() (y∈R,y≠1),所以函数y=
(y∈R,y≠1),所以函数y=![]() (x∈R,且x≠-2)的反函数是f-1=
(x∈R,且x≠-2)的反函数是f-1=![]() (x∈R,x≠1).
(x∈R,x≠1).
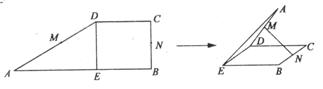 12.设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
12.设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
解:如左图,在平面AED内作MQ∥AE交ED于Q,则MQ⊥ED,且Q为ED的中点,连结QN,则NQ⊥ED且QN∥EB,QN=EB,∠MQN为二面角A-DE-B的平面角,
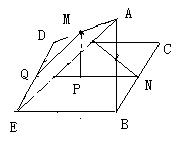 ∴∠MQN=45°∵AB⊥平面BCDE,又∠AEB=∠MQN=45°,MQ=
∴∠MQN=45°∵AB⊥平面BCDE,又∠AEB=∠MQN=45°,MQ=![]() AE=
AE=![]() EB,在平面MQN内作MP⊥BQ,得QP=MP=
EB,在平面MQN内作MP⊥BQ,得QP=MP=![]() EB,故PB=QP=
EB,故PB=QP=![]() EB,故QMN是以∠QMN为直角的等腰三角形,即MN⊥QM,也即MN子AE所成角大小等于90°
EB,故QMN是以∠QMN为直角的等腰三角形,即MN⊥QM,也即MN子AE所成角大小等于90°
13.过双曲线![]() 的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________.
的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________.
解:由题意可得![]() ,即c2-a2=a2+ac,化成关于e的方程e2-e-2=0,解得e=2
,即c2-a2=a2+ac,化成关于e的方程e2-e-2=0,解得e=2
12.从集合![]() 与
与![]() 中各任取2个元素排成一排(字母和数字均不能重复).每排中字母Q和数字0至多只能出现一个的不同排法种数是_________.(用数字作答)
中各任取2个元素排成一排(字母和数字均不能重复).每排中字母Q和数字0至多只能出现一个的不同排法种数是_________.(用数字作答)
解:分三种情况:情况1.不含Q、0的排列:![]() ;情况2.0、Q中只含一个元素Q的排列:
;情况2.0、Q中只含一个元素Q的排列:![]() ;情况3.只含元素0的排列:
;情况3.只含元素0的排列:![]() .综上符合题意的排法种数为
.综上符合题意的排法种数为
![]() +
+![]() +
+![]() =5832
=5832
三、解答题:本大题共6小题,每小题14分,共84分。解答应写出文字说明,证明过程或演算步骤。
15.已知函数![]() .
.
(Ⅰ)
求![]() 的值;
的值;
(Ⅱ)
设![]() ,求
,求![]() 的值.
的值.
解:(Ⅰ)∵f(x)=sin2x+cos2x,∴![]()
(Ⅱ)![]()
![]() ,
,![]()
![]() ,∵α∈(0,π),∴sinα>0,故sinα=
,∵α∈(0,π),∴sinα>0,故sinα=![]()
16.已知实数![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]() ,求
,求![]() .
.
解: 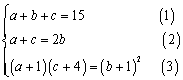
由(1)(2)两式,解得b=5,将c=10-a代入(3),整理得a2-13a+22=0,解得a=2或a=11.
故a=2,b=5,c=11或a=11,b=5,c=-1.经验算,上述两组数符合题意.
17.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,共摸5次.(i)恰好有3次摸到红球的概率;(ii)第一次、第三次、第五次摸到红球的概率.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是![]() ,求p的值.
,求p的值.
解:(Ⅰ)(i)![]()
(ii)![]()
(iii)设袋子A中有m个球,则袋子B中有2m个球,
由 ,得p=
,得p=![]() .
.
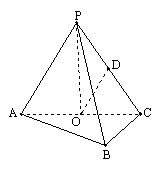
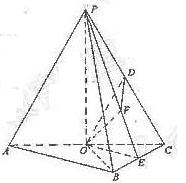
18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=![]() PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证:OD∥平面PAB;
(Ⅱ) 求直线OD与平面PBC所成角的大小.
解:解法一
(Ⅰ)∵O、D分别为AC、PC的中点:∴OD∥PA,又AC![]() 平面PAB,∴OD∥平面PAB.
平面PAB,∴OD∥平面PAB.
(Ⅱ)∵AB⊥BC,OA=OC,∴OA=OC=OB,又∵OP⊥平面ABC,∴PA=PB=PC.
取BC中点E,连结PE,则BC⊥平面POE,作OF⊥PE于F,连结DF,则OF⊥平面PBC
∴∠ODF是OD与平面PBC所成的角.
又OD∥PA,∴PA与平面PBC所成角的大小等于∠ODF.
在Rt△ODF中,sin∠ODF=![]() ,∴PA与平面PBC所成角为arcsin
,∴PA与平面PBC所成角为arcsin![]()
解法二:
∵OP⊥平面ABC,OA=OC,AB=BC,∴OA⊥OB,OA⊥OP,OB⊥OP.
以O为原点,射线OP为非负x轴,建立空间坐标系O-xyz如图),设AB=a,则A(![]() a,0,0).
a,0,0).
B(0, ![]() a,0),C(-
a,0),C(-![]() a,0,0).设OP=h,则P(0,0,h).
a,0,0).设OP=h,则P(0,0,h).
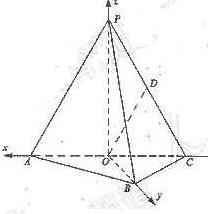
(Ⅰ)∵D为PC的中点,∴![]() 又
又![]() ∥
∥![]() ,
,
∴OD∥平面PAB.
(Ⅱ)∵k=![]() 则PA=2a,∴h=
则PA=2a,∴h=![]() ∴
∴![]() 可求得平面PBC的法向量
可求得平面PBC的法向量![]()
∴cos![]() .
.
设PA与平面PBC所成角为θ,刚sinθ=cos(![]() )=
)=![]() .
.
∴PA与平面PBC所成的角为arcsin![]() .
.
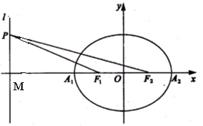 19.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,MA1∶A1F1=2∶1.
19.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,MA1∶A1F1=2∶1.
(Ⅰ)求椭圆的方程;
(Ⅱ)若点P为l上的动点,求∠F1PF2最大值.
解:(Ⅰ)设椭圆的方程为![]() (a>0,b>0),半焦距为c,则MA1=
(a>0,b>0),半焦距为c,则MA1=![]() ,A1F1=a-c
,A1F1=a-c
由题意,得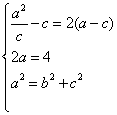 ∴a=2,b=
∴a=2,b=![]() ,c=1.
,c=1.
故椭圆的方程为![]()
(Ⅱ)设P(-4,y0),y0≠0,
∴只需求tan∠F1PF2的最大值即可.
设直线PF1的斜率k1=![]() ,直线PF2的斜率k2=
,直线PF2的斜率k2=![]() ,
,
∵0<∠F1PF2<∠PF1M<![]() ,∴∠F1PF2为锐角.
,∴∠F1PF2为锐角.
∴tan∠F1PF2=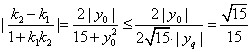
当且仅当![]() ,即y0=
,即y0=![]() 时,tan∠F1PF2取到最大值此时∠F1PF2最大,∴
时,tan∠F1PF2取到最大值此时∠F1PF2最大,∴
∠F1PF2的最大值为arctan![]() .
.
20.已知函数![]() 和
和![]() 的图象关于原点对称,且
的图象关于原点对称,且![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)解不等式![]() ;
;
(Ⅲ)若![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
解:解:(Ⅰ)设函数y=f(x)的图象上任一点Q(xqλ,yq关于原点的对称点(x,y),
则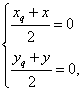 即
即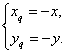 ∵点Qxq,yq)在函数f(x)的图象上,
∵点Qxq,yq)在函数f(x)的图象上,
∴-y=-x2+2x.,故g(x)=-x2+2x
(Ⅱ)由g(x)≥f(x)-x-1可得2x2-x-1≤0,当x≥1时,2x2-x+1≤0,此时不等式无解,
当x<1时,2x2+x-1≤0,∴-1≤x≤![]() ,因此,原不等式的解集为[-1,
,因此,原不等式的解集为[-1,![]() ]
]
(Ⅲ)h(x)=-(1+λ)x2+2(1-λ)x+1
① 当λ=-1时,h(x)=4x+1在[-1,1]上是增函数,∴λ=-1
② 当λ≠-1时,对称轴的方程为x=![]() .
.
(i)
当λ<-1时, ![]() ≤-1,解得λ<-1.
≤-1,解得λ<-1.
(ii)
当λ>-1时, ![]() ≥-1,解得-1<λ≤0.
≥-1,解得-1<λ≤0.
综上,λ≤0