高考数学普通高等学校招生全国统一考试52
第I卷（A）
一、选择题：
（1）设集合
，
，
则集合
中元素的个数为（ ）
（A）1 （B）2 （C）3 （D）4
（2）函数
的最小正周期是（ ）
（A）
（B）
（C）
（D）
（3）设数列
是等差数列，
，Sn是数列的前n项和，则（ ）
（A）S4＜S5 （B）S4＝S5 （C）S6＜S5 （D）S6＝S5
（4）圆
在点
处的切线方程是（ ）
（A）
（B）
（C）
（D）
（5）函数
的定义域是( )
（A）[-
,-1]
(1,) （B）(-,-1)(1,)
（C）[-2,-1](1,2)
（D）(-2,-1)(1,2)
（6）设复数
的幅角的主值为
，虚部为
，则
（ ）
（A）
（B）
（C） 
（D）
（7）设双曲线的焦点在
轴上，两条渐近线为
，则双曲线的离心率
（ ）
（A） 5 （B） 
（C） 
（D） 
（8）不等式
的解集为（ ）
（A）
（B）
（C）
（D）
（9）正三棱柱的底面边长为2，侧面均为直角三角形，则此三棱柱的体积为（ ）
（A）
（B） （C） 
（D） 
（10）在
中，
，则边
上的高为（ ）
（A）
（B） 
（C） 
（D）
（11）设函数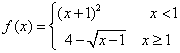
，则使得f(x)
1的自变量x的取值范围为( )
（A）(-∞,-2)[0,10]
（B）(-∞,-2)[0,1]
（C）(-∞,-2)[1,10] （D）[-2,0][1,10]
（12）4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（ ）
（A）12 种 （B）24种 （C）36种 （D）48种
第Ⅱ卷
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
（13）用平面
截半径为R的球，如果球心到截面的距离为
，那么截得小圆的面积与球的表面积的比值为__________.
（14）函数
在区间[
]的最小值为__________.
（15）已知函数y=f(x)是奇函数，当x≥0时, f(x)=3x-1，设f(x)的反函数是y=g(x)，则g(-8)=________.
（16）设P为曲线y2=4(x-1)上的一个动点，则点P到点(0,1)的距离与点P到y轴的距离之和的最小值为__________.
三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤.
（17）（本小题满分12分）已知为锐角，且tg=
，求
的值.
（18）（本小题满分12分）解方程4x+1-2x=11.
（19）（本小题满分12分）某村计划建造一个室内面积为 800m2的矩形蔬菜温室．在温室内，沿左、右两侧与后侧内墙各保留 lm 宽的通道，沿前侧内墙保留3m宽的空地．当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？
（20）（本小题满分12分）三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3.
(1)求证 AB⊥BC ；
(II)如果 AB=BC=2，求AC与侧面PAC所成角的大小．
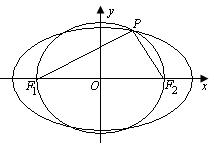
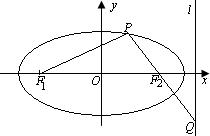
(21) (本小题满分12分)设椭圆
的两个焦点是 F1(-c,0),
F2(c,0)(c>0)，且椭圆上存在点P，使得直线 PF1与直线PF2垂直．
(I)求实数 m 的取值范围．
(II)设l是相应于焦点 F2的准线，直线PF2与l相交于点Q. 若
，求直线PF2的方程．
(22)（本小题满分14分）已知数列{an}的前n项和Sn满足：Sn=2an +(-1)n,n≥1.
⑴写出求数列{an}的前3项a1,a2,a3；
⑵求数列{an}的通项公式；
⑶证明：对任意的整数m>4，有
.
答 案
一、选择题：
BCBDA ACDCB AC
二、填空题：
（13）3:16 （14）1 （15）-2 （16）
三、解答题：
（17）解：∵
,为锐角 ∴
∴
.
（18）解：当x≤0时, 有：4x+1-2x=11
化简得：(2x)2-2x-10=0
解之得：
或
(舍去).
又∵x≤0得2x≤1, 故不可能舍去.
当x<0时, 有：4x-1+2x=11
化简得：(2x)2+2x-12=0
解之得：2x=3或2x= -4(舍去)
∴2x=3 x=log23
综上可得原方程的解为x=log23.
（19）解：设温室的长为xm，则宽为
，由已知得蔬菜的种植面积S为：
(当且仅当
即x=20时，取“＝”).
故：当温室的长为20m, 宽为40m时，蔬菜的种植面积最大，最大面积为648m2.
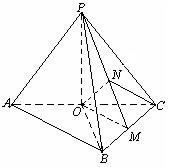（20）⑴证明：取AC中点O, 连结PO、BO.
∵PA＝PC ∴PO⊥AC
又∵侧面PAC⊥底面ABC
∴PO⊥底面ABC
又PA＝PB＝PC ∴AO＝BO＝CO
∴△ABC为直角三角形 ∴AB⊥BC
⑵解：取BC的中点为M，连结OM,PM，所以有OM=AB=，AO=
∴
由⑴有PO⊥平面ABC,OM⊥BC，由三垂线定理得PM⊥BC
∴平面POM⊥平面PBC，又∵PO=OM=.
∴△POM是等腰直角三角形，取PM的中点N，连结ON, NC
则ON⊥PM, 又∵平面POM⊥平面PBC, 且交线是PM, ∴ON⊥平面PBC
∴∠ONC即为AC与平面PBC所成的角.
∴
∴
.
故AC与平面PBC所成的角为
.
（21）解：⑴∵直线PF1⊥直线PF2
∴以O为圆心以c为半径的圆：x2+y2=c2与椭圆：有交点.即
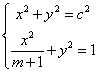有解
又∵c2=a2-b2=m+1-1=m>0
∴
∴
⑵设P(x,y),
直线PF2方程为：y=k(x-c)
∵直线l的方程为：
∴点Q的坐标为(
)
∵ ∴点P分有向线段
所成比为
∵F2(
,0),Q () ∴P(
)
∵点P在椭圆上 ∴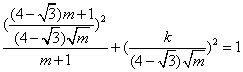
∴
直线PF2的方程为：y=
(x-).
（22）解：⑴当n=1时,有：S1=a1=2a1+(-1)
a1=1；
当n=2时,有：S2=a1+a2=2a2+(-1)2a2=0；
当n=3时,有：S3=a1+a2+a3=2a3+(-1)3a3=2；
综上可知a1=1,a2=0,a3=2；
⑵由已知得：
化简得：
上式可化为：
故数列{
}是以
为首项, 公比为2的等比数列.
故
∴
数列{
}的通项公式为：
.
⑶由已知得：
.
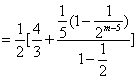
故( m>4).