高考数学普通高等学校招生全国统一考试73

高考数学普通高等学校招生全国统一考试73

试题精析详解

一、选择题（5分12=60分）

1．设集合，则　　 （　　）

　　A．{1}　　　　　　B．{1，2}　　　　 C．{2}　　　　　　D．{0，1，2}

见理科卷1

2．已知　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．　　　　　　 B．－　　　　　 C．　　　　　　D．－

【思路点拨】本题涉及三角函数的有关公式.

【正确解答】由二倍角公式可知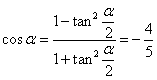，，选B

【解后反思】教材已经给我们提供了一个好的问题情境，并通过“会话”、“协作”初步建构了二倍角公式的概念.我们完全有可能通过进一步的“会话”、协作”，深化对二倍角公式的意义建构，引导学生用学到的“活的思想”去诠释新教材中的新问题.如此去领会、贯彻新教材的构思.

3．的展开式中，含x的正整数次幂的项共有　　　　　　　　　　　（　　）

　　A．4项　　　　　　B．3项　　　　　　C．2项　　　　　　D．1项

见理科卷4

4．函数的定义域为　　　　　　　　　　　　　　　（　　）

　　A．（1，2）∪（2，3）　　　　　　　 B．

　　C．（1，3）　　　 　　　　　　　　　D．[1，3]

【思路点拨】本题涉及求函数定义域的若干知识.在本题中,求定义域要注意两个方面(1)因式有分母,注意分母不能为零,(2)因式有对数,要对数有意义.

【正确解答】由题意可知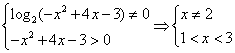，，选A

【解后反思】本题是求定义域的一道常规题目, 函数的定义域（或变量的允许取值范围）看似非常简单,然而在解决问题中若不加以注意,常常会误入歧途,导致失误.此外在用函数方法解决实际问题时,必须要注意到函数定义域的取值范围对实际问题的影响.

5．设函数为　　　　　　　　　（　　）

　　A．周期函数，最小正周期为　　　 B．周期函数，最小正周期为

　　C．周期函数，数小正周期为　　　　D．非周期函数

见理科卷5

6．已知向量　　（　　）

　　A．30°　　　　　 B．60°　　　　　 C．120°　　　　　D．150°

见理科卷6

7．将9个（含甲、乙）平均分成三组，甲、乙分在同一组，则不同分组方法的种数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　 （　　）

　　A．70　　　　　　 B．140　　　　　　C．280　　　　　　D．840

【思路点拨】本题涉及组合的平均分组问题.

【正确解答】要使甲、乙分在同一组，即将剩下的7人分成三组，其中两组有三个人，一组只有一个人，所以要求的概率为，选A

【解后反思】对于平均分组问题,由于各组地位均等,所以平均分成几组,就一定要除以

8．在△ABC中，设命题命题q:△ABC是等边三角形，那么命题p是命题q的　　　　　　 　　　　　　　　　（　　）

　　A．充分不必要条件 B．必要不充分条件

　　C．充分必要条件　　　　　　　　　　 D．既不充分又不必要条件

【思路点拨】本题主要考查三角形形状的判断及充要条件.

【正确解答】，由△ABC是等边三角形，则，显然成立.

：由三角形的性质可知：，又已知，

两式相除得：，令，则，

所以，，得，因此，即△ABC是等边三角形.

因此是的充分必要条件，选C

【解后反思】判断三角形形状,主要根据正弦定理,余弦定理及三角形内角和为,化简有两个方向,(1) 角化边,(2)边化角.

9．矩形ABCD中，AB=4，BC=3，沿AC将矩形ABCD折成一个直二面角B—AC—D，则四面体ABCD的外接球的体积为　　　　　　　　　　　（　　）

　　A．　　　　 B．　　　　 C．　　　　 D．

见理科卷9.

10．已知实数a、b满足等式下列五个关系式：

　　①0<b<a　②a<b<0　③0<a<b  ④b<a<0　⑤a=b

　　其中不可能成立的关系式有　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．1个　　　　　　B．2个　　　　　　C．3个　　　　　　D．4个

见理科卷10.

11．在△OAB中，O为坐标原点，，则当△OAB的面积达最大值时，　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．　　　　　　 B．　　　　　　 C．　　　　　　 D．

见理科卷11

12．为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如右，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a, b的值分别为（　　）

　　A．0,27,78　　　　B．0,27,83　　　　C．2.7,78　　　　 D．2.7,83

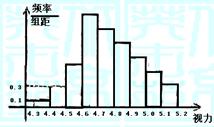
【思路点拨】本题涉及数理统计的若干知识.

【正确解答】由图象可知，前4组的公比为3，最大频率，设后六组公差为，则，解得：，

后四组公差为－0.05， 所以，视力在4.6到5.0之间的学生数为（0.27＋0.22＋0.17＋0.12）×100＝78（人）.选A.

【解后反思】本题是一道数理统计图象题,关于统计一般可分为三步,第一步抽样,第二步根据抽样所得结果,画成图形,第三步根据图形,分析结论.本题是统计的第二步,在此类问题中,可画成两种图形,一个是频率分布直方图,另一个是频率分布条形图,两者有很大的不同,前者是以面积表示频数,频率分布条形图是以高度表示频数.

二、填空题（4分4=16分）

13．若函数是奇函数，则a=　　　　　　　  .

见理科卷13

14．设实数x, y满足　　　　　　   .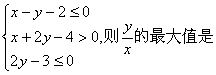

见理科卷14

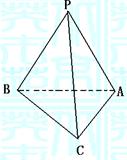
15．如图，在三棱锥P—ABC中，PA=PB=PC=BC，

　　且，则PA与底面ABC所成角为　

　　　　　　　　　  .

【思路点拨】本题主要考查直线与平面所成的角的求法,关键是

确定点P在底面的射影O的位置.

【正确解答】过P作，交底面于O，连结AO并延长交BC于D，连结PD，则PD、AD均垂直于BC，所以AB＝AC，PA与底面ABC所成角为，

设AC＝1，则PA=PB=PC=BC＝，，，

，所以.

【解后反思】熟练掌握三角形的“四心”是快速解该题的关键.外心:三角形三条中垂线的交点,性质外心到三角顶点距离相等,内心:内角平分线的交点,性质是内心到三边距离相等,垂心:三条高线的交点,重心:三条中线的交点,另外记住一些结论也是大有裨益的,比如在三棱锥P-ABC中(1)若P到三个顶点的距离相等,则P在底面的射影是ABC的外心,(2)若P到三边的距离相等,则P在底面的射影是的内心,(3)若则且P在底面的射影是的垂心.

16．以下同个关于圆锥曲线的命题中

　　①设A、B为两个定点，k为非零常数，，则动点P的轨迹为双曲线；

　　②过定圆C上一定点A作圆的动点弦AB，O为坐标原点，若则动点P的轨迹为椭圆；

　　③方程的两根可分别作为椭圆和双曲线的离心率；

　　④双曲线有相同的焦点.

　　其中真命题的序号为　　　　　　　　 （写出所有真命题的序号）

见理科卷16.

三、解答题（本大题共6小题，共74分）

17．（本小题满分12分）

已知函数（a，b为常数）且方程f(x)－x+12=0有两个实根为x₁=3, x₂=4.

　 （1）求函数f(x)的解析式；

　 （2）设k>1，解关于x的不等式；.

见理科卷17.

18．（本小题满分12分）

已知向量.

求函数f(x)的最大值，最小正周期，并写出f(x)在[0，π]上的单调区间.

【思路点拨】本题主要考查向量与三角函数的综合题，正确求出f（x）是解该题的关键.

【正确解答】

　　　　

=.

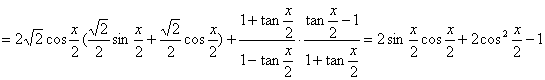
所以，最小正周期为上单调增加，上单调减少.

【解后反思】这是一道向量与三角函数的综合题,向量虽然是近年高中数学出现的新知识,但向量知识却很重要.因为向量是近代数学中重要和基本的数学概念之一,它是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景.在学习过程中,同学将会了解向量丰富的实际背景,逐渐理解平面向量及其运算的意义,一定能要用向量语言和方法表述和解决数学和物理中的一些问题,发展数学运算能力和解决数学实际问题的能力.

19．（本小题满分12分）

A、B两位同学各有五张卡片，现以投掷均匀硬币的形式进行游戏，当出现正面朝上时A赢得B一张卡片，否则B赢得A一张卡片，如果某人已赢得所有卡片，则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.

【思路点拨】本题涉及随机事件的有关概率.

【正确解答】设表示游戏终止时掷硬币的次数，

设正面出现的次数为m，反面出现的次数为n，则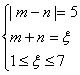，可得：

【解后反思】这是一道比较复杂的概率题目,首先我们应理解随机变量及其概率分布的概念,掌握分布函数F(x)= P{X≤x}的概念及性质;才能会计算与随机变量相关的事件的概率.同时我们在解决的过程中,也适当对此类解题的流程也要有一个清晰的了解,这样才能保证此类题目得高分和全分.

20．（本小题满分12分）

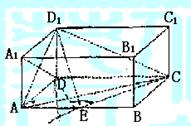
如图，在长方体ABCD—A₁B₁C₁D₁，中，AD=AA₁=1，AB=2，点E在棱AB上移动.

　 （1）证明：D₁E⊥A₁D;

　 （2）当E为AB的中点时，求点E到面ACD₁的距离；

　 （3）AE等于何值时，二面角D₁—EC－D的大小为.

见理科卷20.

21．（本小题满分12分）

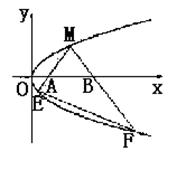如图，M是抛物线上y²=x上的一点，动弦ME、MF分别交x轴于A、B两点，且MA=MB.

　 （1）若M为定点，证明：直线EF的斜率为定值；

　 （2）若M为动点，且∠EMF=90°，求△EMF的重心G的轨迹方程.

【思路点拨】本题涉及抛物线与直线相交的有关知识.

【正确解答】（1）设M（y,y₀），直线ME的斜率为k(l>0)

则直线MF的斜率为－k，

消

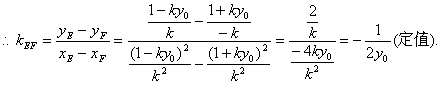
所以直线EF的斜率为定值

（2）

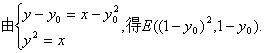
同理可得

设重心G（x, y），则有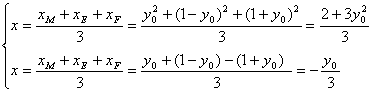

【解后反思】这是一道重要的数学问题,它属于解析几何范畴,几乎是高考数学每年的必考内容之一,此类问题一定要”大胆假设,细心求解”,根据题目要求先将题目所涉及的未知量都可以设出来,然后根据题目把所有的条件都变成等式,一定可以求出来,当然求的过程中,采取适当的小技巧,例如化简或适当分类讨论,可以大为简化过程,而且会尽量多多得分,同时这一类题目也需要很强的计算能力.

22．（本小题满分14分）

已知数列{a_n}的前n项和S_n满足S_n－S_n－2=3求数列{a_n}的通项公式.

【思路点拨】本题涉及数列的若干知识.

【正确解答】方法一：先考虑偶数项有：

　　　 　　　　　　　　　　　　　 

　　　 　　　　　　　　　　　　　　 ………

　　　 　　　　　　　　　　　　　 

　　　

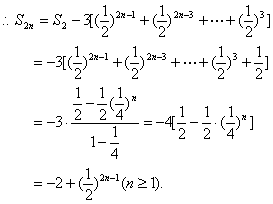
　　　 同理考虑奇数项有：

………

　　　

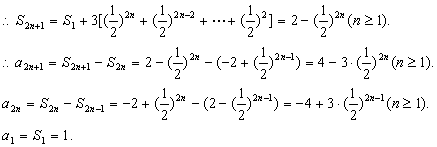
　　　 综合可得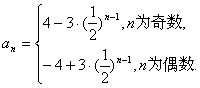

　　　 方法二：因为

　　　 两边同乘以，可得：

令

所以

………

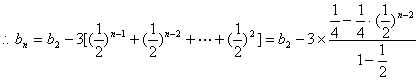
【解后反思】这是本张试卷的压轴大题,有很大的难度,在数列中,属于知道数列的前几项和来求通项公式,我们发现数列的奇数项与偶数项相邻的两个之间的差为等比数列,利用累加法求出前n项求和公式,最后再利用前n项求和公式来求通项公式,通常累加法可以解决数列中相邻两项的差成等比数列或有规律的关系,可以采用累加法来解决.对于高考数学中比较难的题目,我们除了具备深厚的数学知识外,还要加四个能力,一个是阅读理解能力,一个是数学探究能力,一个是应用能力,一个是学习能力. 阅读理解能力即要读懂数学题目所讲的内容,包含题目中的隐含条件, 数学探究能力即就是题目的结论不明确，联想自己过去做的题, 应用能力即将一些数学知识与实际生活的某些方面相结合. 学习能力即题目给BM 一些新的信息,这可以是一个新的定义, ,把这个信息与所学的知识结合起来,这就看谁能够领会,领会以后很快把自己过去的知识结合起来.