高考数学普通高等学校招生全国统一考试121
数 学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3到8页。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:
如果事件A、B互斥,那么 球是表面积公式
![]()
![]()
如果事件A、B相互独立,那么 其中R表示球的半径
![]() 球的体积公式
球的体积公式
如果事件A在一次试验中发生的概率是P,那么 ![]()
n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
![]()
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合![]() ,集合
,集合![]() ,则集合
,则集合![]()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)复数![]() 的虚部为
的虚部为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)已知![]() ,下面结论正确的是
,下面结论正确的是
(A)![]() 在
在![]() 处连续
(B)
处连续
(B)![]()
(C)![]() (D)
(D)![]()
(4)已知二面角![]() 的大小为
的大小为![]() ,
,![]() 为异面直线,且
为异面直线,且![]() ,则
,则![]() 所成的角为
所成的角为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
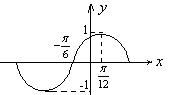 (5)下列函数中,图象的一部分如右图所示的是
(5)下列函数中,图象的一部分如右图所示的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(6)已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹所包围的图形的面积等于
的轨迹所包围的图形的面积等于
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
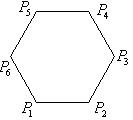
(7) 如图,已知正六边形![]() ,下列向量的数量积中最大的是
,下列向量的数量积中最大的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(8) 某厂生产甲产品每千克需用原料![]() 和原料
和原料![]() 分别为
分别为![]() ,生产乙产品每千克需用原料
,生产乙产品每千克需用原料![]() 和原料
和原料![]() 分别为
分别为![]() 千克,甲、乙产品每千克可获利润分别为
千克,甲、乙产品每千克可获利润分别为![]() 元,月初一次性够进本月用原料
元,月初一次性够进本月用原料![]() 各
各![]() 千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为
千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为![]() 千克,
千克,![]() 千克,月利润总额为
千克,月利润总额为![]() 元,那么,用于求使总利润
元,那么,用于求使总利润![]() 最大的数学模型中,约束条件为
最大的数学模型中,约束条件为
(A) (B)
(B)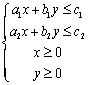 (C)
(C)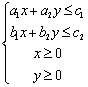 (D)
(D)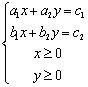
(9) 直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过
两点,过![]() 两点向抛物线的准线作垂线,垂足分别为
两点向抛物线的准线作垂线,垂足分别为![]() ,则梯形
,则梯形![]() 的面积为
的面积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10) 已知球![]() 的半径是
的半径是![]() ,
,![]() 三点都在球面上,
三点都在球面上,![]() 两点和
两点和![]() 两点的球面距离都是
两点的球面距离都是![]() ,
,![]() 两点的球面距离是
两点的球面距离是![]() ,则二面角
,则二面角![]() 的大小是
的大小是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)设![]() 分别是
分别是![]() 的三个内角
的三个内角![]() 所对的边,则
所对的边,则![]() 是
是![]() 的
的
(A)充分条件 (B)充分而不必要条件
(C)必要而充分条件 (D)既不充分又不必要条件
(12)从![]() 到
到![]() 这
这![]() 个数字中任取
个数字中任取![]() 个数字组成一个没有重复数字的三位数,这个数不能被
个数字组成一个没有重复数字的三位数,这个数不能被![]() 整除的概率为
整除的概率为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
第Ⅱ卷
二.填空题:本大题共4小题,每小题4分,共16分;把答案填在题中的横线上。
(13)在三棱锥![]() 中,三条棱
中,三条棱![]() 两两互相垂直,且
两两互相垂直,且![]() 是
是![]() 边的中点,则
边的中点,则![]() 与平面
与平面![]() 所成角的大小是______________(用反三角函数表示)
所成角的大小是______________(用反三角函数表示)
(14)设离散性随机变量![]() 可能取的值为
可能取的值为![]() ,又
,又![]() 的数学期望
的数学期望![]() ,则
,则![]() ________________;
________________;
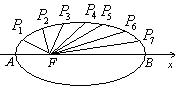 (15)如图,把椭圆
(15)如图,把椭圆![]() 的长轴
的长轴![]() 分成
分成![]() 等份,过每个分点作
等份,过每个分点作![]() 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于![]() 七个点,
七个点,![]() 是椭圆的一个焦点,则
是椭圆的一个焦点,则
![]() _______;
_______;
(16)非空集合![]() 关于运算
关于运算![]() 满足:(1)对任意
满足:(1)对任意![]() ,都有
,都有![]() ;
;
(2)存在![]() ,使得对一切
,使得对一切![]() ,都有
,都有![]() ,则称
,则称![]() 关于运算
关于运算![]() 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:
①![]() ②
②![]()
③![]() ④
④![]()
⑤![]()
其中![]() 关于运算
关于运算![]() 为“融洽集”________________;(写出所有“融洽集”的序号)
为“融洽集”________________;(写出所有“融洽集”的序号)
普通高等学校招生全国统一考试
数 学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3到8页。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题答题卡:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 选项 |
二、填空题答题卡:
⒔ 。⒕ 。⒖ 。⒗ 。
三.解答题 共6个小题,共74分,解答时应写出必要的文字说明,证明过程或演算步骤.
| 得分 | 评卷人 |
17.(本小题满分12分)
已知A、B、C是![]() 三内角,向量
三内角,向量![]()
![]()
且![]()
(Ⅰ)求角A
(Ⅱ)若![]()
| 得分 | 评卷人 |
18.(本小题满分12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都“合格”则该课程考核“合格”。甲、乙、丙三人在理论考核中合格的概率分别为0.9、0.8、0.7;在实验考核中合格的概率分别为0.8、0.7、0.9。所有考核是否合格相互之间没有影响。
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率(结果保留三位小数)。
| 得分 | 评卷人 |
19.(本小题满分12分)
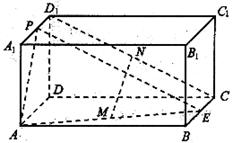
如图,长方体ABCD-![]() 中,E、P分别是BC、
中,E、P分别是BC、![]() 的中点,
的中点,
M、N分别是AE、![]() 的中点,
的中点, ![]()
![]()
 (Ⅰ)求证:
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱锥P-DEN的体积。
| 得分 | 评卷人 |
20.(本小题满分12分)
已知数列![]() ,其中
,其中![]()
![]() 记数列
记数列![]() 的
的
前n项和为![]() 数列
数列![]() 的前n项和为
的前n项和为![]()
(Ⅰ)求![]() ;
;
(Ⅱ) 设![]()
![]() (其中
(其中![]() 为
为![]() 的导函数),
的导函数),
计算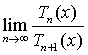
| 得分 | 评卷人 |
21.(本小题满分12分)
已知两定点![]()
![]() 满足条件
满足条件![]() 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。如果
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。如果![]() 且曲线E上存在点C,使
且曲线E上存在点C,使![]() 求
求![]() 。
。
| 得分 | 评卷人 |
22.(本小题满分14分)
已知函数![]() f(x)的导函数是
f(x)的导函数是![]() 。对任意两个不相等的正数
。对任意两个不相等的正数![]() ,证明:
,证明:
(Ⅰ)当![]() 时,
时,![]() ;
;
(Ⅱ)当![]() 时,
时,![]() 。
。
2006年普通高等学校招生全国统一考试
(四川卷)理科数学及参考答案
一.选择题:本大题共12小题,每小题5分,共60分;
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | D | B | D | B | A | C | A | C | A | B |
二、填空题
(13)![]() (14)
(14)![]() (15)35 (16)①,③
(15)35 (16)①,③
三.解答题:本大题共6小题,共74分;解答应写出文字说明,证明过程或演算步骤。
(17)(本大题满分12分)
已知![]() 是三角形
是三角形![]() 三内角,向量
三内角,向量![]() ,且
,且![]()
(Ⅰ)求角![]() ;
;
(Ⅱ)若![]() ,求
,求![]()
本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式以及倍角公式,考察应用、分析和计算能力。满分12分。
解:(Ⅰ)∵![]() ∴
∴![]() 即
即![]()
![]() ,
, ![]()
∵![]() ∴
∴![]() ∴
∴![]()
(Ⅱ)由题知![]() ,整理得
,整理得![]()
∴![]() ∴
∴![]()
∴![]() 或
或![]()
而![]() 使
使![]() ,舍去
∴
,舍去
∴![]()
∴![]()
![]()
![]()
![]()
![]()
(18)(本大题满分12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”则该课程考核“合格”,甲、乙、丙三人在理论考核中合格的概率分别为![]() ;在实验考核中合格的概率分别为
;在实验考核中合格的概率分别为![]() ,所有考核是否合格相互之间没有影响
,所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)
本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法,考察应用概率知识解决实际问题的能力。满分12分。
解:记“甲理论考核合格”为事件![]() ;“乙理论考核合格”为事件
;“乙理论考核合格”为事件![]() ;“丙理论考核合格”为事件
;“丙理论考核合格”为事件![]() ;记
;记![]() 为
为![]() 的对立事件,
的对立事件,![]() ;记“甲实验考核合格”为事件
;记“甲实验考核合格”为事件![]() ;“乙实验考核合格”为事件
;“乙实验考核合格”为事件![]() ;“丙实验考核合格”为事件
;“丙实验考核合格”为事件![]() ;
;
(Ⅰ)记“理论考核中至少有两人合格”为事件![]() ,记
,记![]() 为
为![]() 的对立事件
的对立事件
解法1:![]()
![]()
![]()
![]()
解法2:![]()
![]()
![]()
![]()
![]()
![]()
所以,理论考核中至少有两人合格的概率为![]()
(Ⅱ)记“三人该课程考核都合格” 为事件![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以,这三人该课程考核都合格的概率为![]()
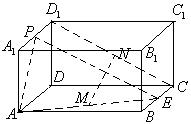 (19)(本大题满分12分)
(19)(本大题满分12分)
如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别是
分别是![]() 的中点,
的中点,![]()
(Ⅰ)求证:![]() 面
面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
(Ⅲ)求三棱锥![]() 的体积。
的体积。
本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。满分12分
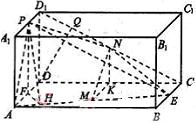 解法一:(Ⅰ)证明:取
解法一:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连结
,连结![]()
∵![]() 分别为
分别为![]() 的中点
的中点
∵![]()
∴![]() 面
面![]() ,
,![]() 面
面![]()
∴面![]() 面
面![]() ∴
∴![]() 面
面![]()
(Ⅱ)设![]() 为
为![]() 的中点
的中点
∵![]() 为
为![]() 的中点
∴
的中点
∴![]() ∴
∴![]() 面
面![]()
作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,则由三垂线定理得
,则由三垂线定理得![]()
从而![]() 为二面角
为二面角![]() 的平面角。
的平面角。
在![]() 中,
中,![]() ,从而
,从而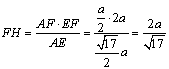
在![]() 中,
中,![]()
故:二面角![]() 的大小为
的大小为![]()
(Ⅲ)![]()
作![]() ,交
,交![]() 于
于![]() ,由
,由![]() 面
面![]() 得
得![]()
∴![]() 面
面![]()
∴在![]() 中,
中,![]()
∴![]()
![]()
![]()
方法二:以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立直角坐标系,则
轴,建立直角坐标系,则![]()
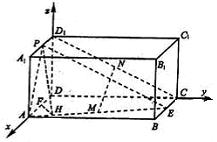 ∵
∵![]() 分别是
分别是![]() 的中点
的中点
∴![]()
(Ⅰ)![]()
取![]() ,显然
,显然![]() 面
面![]()
![]() ,∴
,∴![]()
又![]() 面
面![]() ∴
∴![]() 面
面![]()
(Ⅱ)过![]() 作
作![]() ,交
,交![]() 于
于![]() ,取
,取![]() 的中点
的中点![]() ,则
,则![]() ∵
∵
设![]() ,则
,则![]()
又![]()
由![]() ,及
,及![]() 在直线
在直线![]() 上,可得:
上,可得: 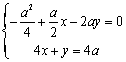
解得![]()
∴![]() ∴
∴![]() 即
即![]()
∴![]() 与
与![]() 所夹的角等于二面角
所夹的角等于二面角![]() 的大小
的大小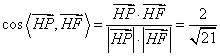
故:二面角![]() 的大小为
的大小为![]()
(Ⅲ)设![]() 为平面
为平面![]() 的法向量,则
的法向量,则![]()
又![]()
∴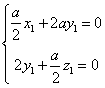 即
即 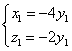 ∴可取
∴可取![]()
∴![]() 点到平面
点到平面![]() 的距离为
的距离为
∵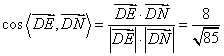 ,
, ![]()
∴![]()
∴![]()
(20)(本大题满分12分)
已知数列![]() ,其中
,其中![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]()
(Ⅰ)求![]() ;
;
(Ⅱ)设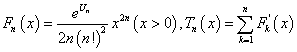 ,(其中
,(其中![]() 为
为![]() 的导函数),计算
的导函数),计算![]()
本小题主要考察等差数列、等比数列的基础知识,以及对数运算、导数运算和极限运算的能力,同时考查分类讨论的思想方法,满分12分。
解:(Ⅰ)由题意,![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列 前
的等差数列 前![]() 项和
项和![]() ,
,![]()
![]()
(Ⅱ)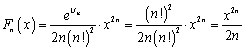
![]()
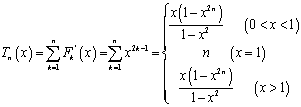
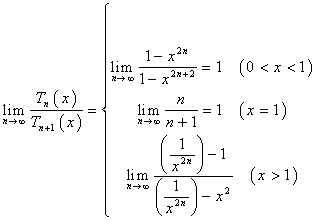
(21)(本大题满分14分)
已知两定点![]() ,满足条件
,满足条件![]() 的点
的点![]() 的轨迹是曲线
的轨迹是曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,如果
两点,如果![]() ,且曲线
,且曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,求
,求![]() 的值和
的值和![]() 的面积
的面积![]()
本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力。满分12分。
解:由双曲线的定义可知,曲线![]() 是以
是以![]() 为焦点的双曲线的左支,
为焦点的双曲线的左支,
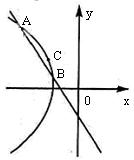 且
且![]() ,易知
,易知![]()
故曲线![]() 的方程为
的方程为![]()
设![]() ,由题意建立方程组
,由题意建立方程组![]()
消去![]() ,得
,得![]()
又已知直线与双曲线左支交于两点![]() ,有
,有
 解得
解得![]()
又∵ ![]()
![]()
![]()
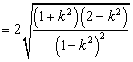
依题意得 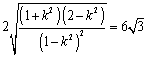 整理后得
整理后得 ![]()
∴![]() 或
或![]() 但
但![]() ∴
∴![]()
故直线![]() 的方程为
的方程为![]()
设![]() ,由已知
,由已知![]() ,得
,得![]()
∴![]() ,
,![]()
又![]() ,
,![]()
∴点![]()
将点![]() 的坐标代入曲线
的坐标代入曲线![]() 的方程,得
的方程,得![]()
得![]() ,但当
,但当![]() 时,所得的点在双曲线的右支上,不合题意
时,所得的点在双曲线的右支上,不合题意
∴![]() ,
,![]() 点的坐标为
点的坐标为![]()
![]() 到
到![]() 的距离为
的距离为
∴![]() 的面积
的面积![]()
(22)(本大题满分14分)
已知函数![]() ,
,![]() 的导函数是
的导函数是![]() ,对任意两个不相等的正数
,对任意两个不相等的正数![]() ,证明:
,证明:
(Ⅰ)当![]() 时,
时,![]()
(Ⅱ)当![]() 时,
时,![]()
本小题主要考查导数的基本性质和应用,函数的性质和平均值不等式等知识及综合分析、推理论证的能力,满分14分。
证明:(Ⅰ)由![]()
得![]()
![]()
![]()
而![]() ①
①
又![]()
∴![]() ②
②
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() ③
③
由①、②、③得
![]()
即![]()
(Ⅱ)证法一:由![]() ,得
,得![]()
∴![]()
![]()
![]()
下面证明对任意两个不相等的正数![]() ,有
,有![]() 恒成立
恒成立
即证![]() 成立
成立
∵![]()
设![]() ,则
,则![]()
令![]() 得
得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
![]() ∴
∴![]()
∴对任意两个不相等的正数![]() ,恒有
,恒有![]()
证法二:由![]() ,得
,得![]()
∴![]()

∵![]() 是两个不相等的正数
是两个不相等的正数
∴
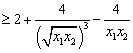
设![]() ,
,![]()
则![]() ,列表:
,列表:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
∴![]() 即
即 ![]()
∴![]()
即对任意两个不相等的正数![]() ,恒有
,恒有![]()