高考数学普通高等学校招生全国统一考试89
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至4页。全卷满分150分，考试时间120分钟。
考生注意事项：
1.答题前，务必在试题卷、答题卡规定的地方填写自己的座位号、姓名，并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。
2．答第Ⅰ卷时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。
3．答第Ⅱ卷时，必须用0.5毫米墨水签字笔在答题卡上书写。在试题卷上作答无效。
4．考试结束，监考人员将试题卷和答题卡一并收回。
参考公式：
如果时间A、B互斥，那么
如果时间A、B相互独立，那么
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式
，其中R表示球的半径
球的体积公式
，其中R表示球的半径
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1、已知集合M＝｛x
｝，N＝｛yy＝3x2＋1，xÎR｝，则MÇN＝（ C ）
A．Æ B. {xx³1} C.｛xx>1｝ D. {x x³1或x<0}
解：M＝｛xx>1或x£0｝，N＝｛yy³1｝故选C
2、已知复数z满足（
＋3i）z＝3i，则z＝（ D ）
A．
B. 
C. 
D.
解：
故选D
3、若a>0，b>0，则不等式－b<
<a等价于（ D ）
A．
<x<0或0<x<
B.－<x<
C.x<-或x> D.x<或x>
解：
故选D
4、设O为坐标原点，F为抛物线y2＝4x的焦点，A是抛物线上一点，若
＝－4
则点A的坐标是（B ）
A．（2，±2
） B. (1，±2) C.（1，2）D.(2，2)
解：F（1，0）设A（
，y0）则
＝（ ，y0），
＝（1－，－y0），由
· ＝－4Þy0＝±2，故选B
5、对于R上可导的任意函数f（x），若满足（x－1）
³0，则必有（ C ）
A． f（0）＋f（2）<2f（1） B. f（0）＋f（2）£2f（1）
C. f（0）＋f（2）³2f（1） D. f（0）＋f（2）>2f（1）
解：依题意，当x³1时，f¢（x）³0，函数f（x）在（1，＋¥）上是增函数；当x<1时，f¢（x）£0，f（x）在（－¥，1）上是减函数，故f（x）当x＝1时取得最小值，即有
f（0）³f（1），f（2）³f（1），故选C
6、若不等式x2＋ax＋1³0对于一切xÎ（0，
）成立，则a的最小值是（ C ）
A．0 B. –2 C.-
D.-3
解：设f（x）＝x2＋ax＋1，则对称轴为x＝
若³，即a£－1时，则f（x）在〔0，〕上是减函数，应有f（）³0Þ
－£x£－1
若£0，即a³0时，则f（x）在〔0，〕上是增函数，应有f（0）＝1>0恒成立，故a³0
若0££，即－1£a£0，则应有f（）＝
恒成立，故－1£a£0
综上，有－£a故选C
7、已知等差数列｛an｝的前n项和为Sn，若
，且A、B、C三点共线（该直线不过原点O），则S200＝（ A ）
A．100 B. 101 C.200 D.201
解：依题意，a1＋a200＝1，故选A
8、在（x－）2006 的二项展开式中，含x的奇次幂的项之和为S，当x＝时，S等于（B ）
A.23008 B.-23008 C.23009 D.-23009
解：设（x－）2006＝a0x2006＋a1x2005＋…＋a2005x＋a2006
则当x＝时，有a0（）2006＋a1（）2005＋…＋a2005（）＋a2006＝0 （1）
当x＝－时，有a0（）2006－a1（）2005＋…－a2005（）＋a2006＝23009 （2）
（1）－（2）有a1（）2005＋…＋a2005（）＝－23009¸2＝－23008
故选B
9、P是双曲线
的右支上一点，M、N分别是圆（x＋5）2＋y2＝4和（x－5）2＋y2＝1上的点，则PM－PN的最大值为（ D ）
A. 6 B.7 C.8 D.9
解：设双曲线的两个焦点分别是F1（－5，0）与F2（5，0），则这两点正好是两圆的圆心，当且仅当点P与M、F1三点共线以及P与N、F2三点共线时所求的值最大，此时
PM－PN＝（PF1－2）－（PF2－1）＝10－1＝9故选B
10、将7个人（含甲、乙）分成三个组，一组3人，另两组2 人，不同的分组数为a，甲、乙分到同一组的概率为p，则a、p的值分别为（ A ）
A．
a=105 p=
B.a=105 p=
C.a=210 p= D.a=210 p=
解：a＝
＝105
甲、乙分在同一组的方法种数有
（1）
若甲、乙分在3人组，有
＝15种
（2）
若甲、乙分在2人组，有
＝10种，故共有25种，所以P＝
故选A
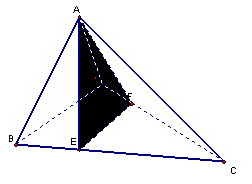
11、如图，在四面体ABCD中，截面AEF经过四面体的内切球（与四个面都相切的球）球心O，且与BC，DC分别截于E、F，如果截面将四面体分成体积相等的两部分，设四棱锥A－BEFD与三棱锥A－EFC的表面积分别是S1，S2，则必有（ ）
A. S1<S2
B. S1>S2
C.
S1=S2
D. S1，S2的大小关系不能确定
解：连OA、OB、OC、OD
则VA－BEFD＝VO－ABD＋VO－ABE＋VO－BEFD
VA－EFC＝VO－ADC＋VO－AEC＋VO－EFC又VA－BEFD＝VA－EFC而每个三棱锥的高都是原四面体的内切球的半径，故SABD＋SABE＋SBEFD＝SADC＋SAEC＋SEFC又面AEF公共，故选C
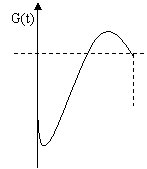
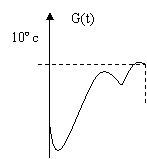
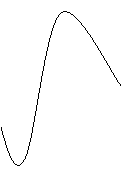
12、某地一年的气温Q（t）（单位：ºc）与时间t（月份）之间的关系如图（1）所示，已知该年的平均气温为10ºc，令G（t）表示时间段〔0,t〕的平均气温，G（t）与t之间的函数关系用下列图象表示，则正确的应该是（ A ）
 |  | ||
|
|
 | |||
 | |||
|
|
|
|
|
|
|
| ||||
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
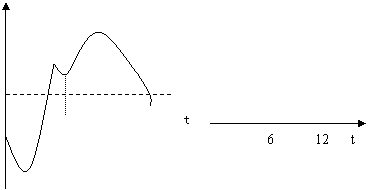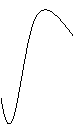
解：结合平均数的定义用排除法求解
理科数学
第Ⅱ卷（非选择题 共90分）
注意事项：
请用0.5毫米黑色墨水签字笔在答题卡上书写作答，在试题卷上书写作答无效。
二、填空题：本大题共4小题，每小题4分，共16分，把答案填写在答题卡的相应位置。
13、数列｛
｝的前n项和为Sn，则
Sn＝
解：
故
14、设f（x）＝log3（x＋6）的反函数为f－1（x），若〔f－1（m）＋6〕〔f－1（n）＋6〕＝27
则f（m＋n）＝___________________
解：f－1（x）＝3x－6故〔f－1（m）＋6〕·〔f－1（x）＋6〕＝3m·3n＝3m ＋n＝27
\m＋n＝3\f（m＋n）＝log3（3＋6）＝2
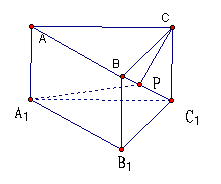
15、如图，在直三棱柱ABC－A1B1C1中，底面为直角三角形，ÐACB＝90°，AC＝6，BC＝CC1＝，P是BC1上一动点，则CP＋PA1的最小值是___________
解：连A1B，沿BC1将△CBC1展开与△A1BC1在同一个平面内，如图所示，
|
|
|
|
连A1C，则A1C的长度就是所求的最小值。
通过计算可得ÐA1C1C＝90°又ÐBC1C＝45°
\ÐA1C1C＝135° 由余弦定理可求得A1C＝
16、已知圆M：（x＋cosq）2＋（y－sinq）2＝1，
直线l：y＝kx，下面四个命题：
（A） 对任意实数k与q，直线l和圆M相切；
（B） 对任意实数k与q，直线l和圆M有公共点；
（C） 对任意实数q，必存在实数k，使得直线l与
和圆M相切
（D）对任意实数k，必存在实数q，使得直线l与
和圆M相切
其中真命题的代号是______________（写出所有真命题的代号）
解：圆心坐标为（－cosq，sinq）d＝
故选（B）（D）
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤
17、（本小题满分12分）
已知函数f（x）＝x3＋ax2＋bx＋c在x＝－
与x＝1时都取得极值
（1） 求a、b的值与函数f（x）的单调区间
（2） 若对xÎ〔－1，2〕，不等式f（x）<c2恒成立，求c的取值范围。
解：（1）f（x）＝x3＋ax2＋bx＋c，f¢（x）＝3x2＋2ax＋b
由f¢（
）＝
，f¢（1）＝3＋2a＋b＝0得
a＝
，b＝－2
f¢（x）＝3x2－x－2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：
| x | （－¥，－ | － | （－ | 1 | （1，＋¥） |
| f¢（x） | ＋ | 0 | － | 0 | ＋ |
| f（x） | | 极大值 | ¯ | 极小值 | |
所以函数f（x）的递增区间是（－¥，－）与（1，＋¥）
递减区间是（－，1）
（2）f（x）＝x3－x2－2x＋c，xÎ〔－1，2〕，当x＝－时，f（x）＝
＋c
为极大值，而f（2）＝2＋c，则f（2）＝2＋c为最大值。
要使f（x）<c2（xÎ〔－1，2〕）恒成立，只需c2>f（2）＝2＋c
解得c<－1或c>2
18、（本小题满分12分）
某商场举行抽奖促销活动，抽奖规则是：从装有9个白球，1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球可获得奖金10元；摸出2个红球可获得奖金50元，现有甲，乙两位顾客，规定：甲摸一次，乙摸两次，令x表示甲，乙摸球后获得的奖金总额。求：
（1）x的分布列 （2）x的的数学期望
解：（1）x的所有可能的取值为0，10，20，50，60
分布列为
| x | 0 | 10 | 20 | 50 | 60 |
| P |
|
|
|
|
|
(2)Ex＝3.3
19、（本小题满分12分）
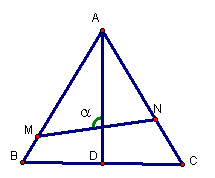
如图，已知△ABC是边长为1的正三角形，M、N分别是
边AB、AC上的点，线段MN经过△ABC的中心G，
设ÐMGA＝a（
）
（1） 试将△AGM、△AGN的面积（分别记为S1与S2）
表示为a的函数
（2）
求y＝
的最大值与最小值
解：(1)因为G是边长为1的正三角形ABC的中心，
所以 AG＝
，ÐMAG＝
，
由正弦定理
,得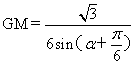
则S1＝GM·GA·sina＝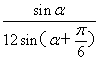
,
同理可求得S2＝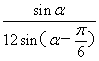
.
(2)y＝
＝
＝72（3＋cot2a）因为，所以当a＝
或a＝
时，y取得最大值ymax＝240
当a＝
时，y取得最小值ymin＝216
20、（本小题满分12分）
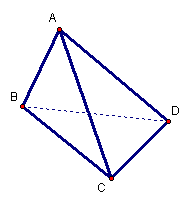
如图，在三棱锥A－BCD中，侧面ABD、ACD
是全等的直角三角形，AD是公共的斜边，
且AD＝，BD＝CD＝1，另一个侧面是正三角形
（1） 求证：AD^BC
（2） 求二面角B－AC－D的大小
（3） 在直线AC上是否存在一点E，使ED与面BCD
成30°角？若存在，确定E的位置；若不存在，说明理由。
20、解法一：
（1）
方法一：作AH^面BCD于H，连DH。
AB^BDÞHB^BD，又AD＝，BD＝1
\AB＝＝BC＝AC \BD^DC
又BD＝CD，则BHCD是正方形，则DH^BC\AD^BC
方法二：取BC的中点O，连AO、DO
则有AO^BC，DO^BC，\BC^面AOD
\BC^AD
（2）
作BM^AC于M，作MN^AC交AD于N，则ÐBMN就是二面角B－AC－D的平面角，因为AB＝AC＝BC＝\M是AC的中点，且MN¤¤CD，则BM＝
，MN＝CD＝，BN＝AD＝
，由余弦定理可求得cosÐBMN＝
\ÐBMN＝arccos
（3）
设E是所求的点，作EF^CH于F，连FD。则EF¤¤AH，\EF^面BCD，ÐEDF就是ED与面BCD所成的角，则ÐEDF＝30°。设EF＝x，易得AH＝HC＝1，则CF＝x，FD＝
，\tanÐEDF＝
＝
＝
解得x＝
，则CE＝x＝1
故线段AC上存在E点，且CE＝1时，ED与面BCD成30°角。
解法二：此题也可用空间向量求解，解答略
21、（本大题满分12分）
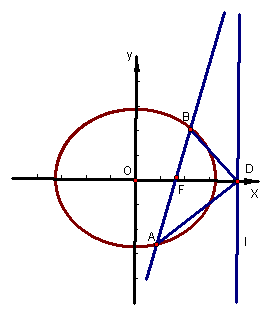
如图，椭圆Q：
（a>b>0）的右焦点F（c，0），过点F的一动直线m绕点F转动，并且交椭圆于A、B两点，P是线段AB的中点
（1） 求点P的轨迹H的方程
（2） 在Q的方程中，令a2＝1＋cosq＋sinq，b2＝sinq（0<q£ ），确定q的值，使原点距椭圆的右准线l最远，此时，设l与x轴交点为D，当直线m绕点F转动到什么位置时，三角形ABD的面积最大？
21、解：如图，（1）设椭圆Q：（a>b>0）
上的点A（x1，y1）、B（x2，y2），又设P点坐标为P（x，y），则
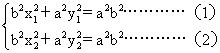
1°当AB不垂直x轴时，x1¹x2，
由（1）－（2）得
b2（x1－x2）2x＋a2（y1－y2）2y＝0
\b2x2＋a2y2－b2cx＝0…………（3）
2°当AB垂直于x轴时，点P即为点F，满足方程（3）
故所求点P的轨迹方程为：b2x2＋a2y2－b2cx＝0
（2）因为，椭圆 Q右准线l方程是x＝
，原点距l
的距离为，由于c2＝a2－b2，a2＝1＋cosq＋sinq，b2＝sinq（0<q£）
则＝
＝2sin（
＋
）
当q＝时，上式达到最大值。此时a2＝2，b2＝1，c＝1，D（2，0），DF＝1
设椭圆Q：
上的点 A（x1，y1）、B（x2，y2），三角形ABD的面积
S＝y1＋y2＝y1－y2
设直线m的方程为x＝ky＋1，代入中，得（2＋k2）y2＋2ky－1＝0
由韦达定理得y1＋y2＝
，y1y2＝
，
4S2＝（y1－y2）2＝（y1＋y2）2－4 y1y2＝
令t＝k2＋1³1，得4S2＝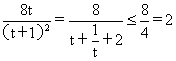
，当t＝1，k＝0时取等号。
因此，当直线m绕点F转到垂直x轴位置时，三角形ABD的面积最大。
22、（本大题满分14分）
已知数列｛an｝满足：a1＝
，且an＝
（1） 求数列｛an｝的通项公式；
（2） 证明：对于一切正整数n，不等式a1·a2·……an<2·n！
22、解：
（1）
将条件变为：1－
＝
，因此｛1－｝为一个等比数列，其首项为
1－
＝
，公比，从而1－＝
，据此得an＝
（n³1）…………1°
（2）
证：据1°得，a1·a2·…an＝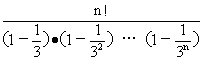
为证a1·a2·……an<2·n！
只要证nÎN*时有
>…………2°
显然，左端每个因式都是正数，先证明，对每个nÎN*，有
³1－（
）…………3°
用数学归纳法证明3°式：
（i） n＝1时，3°式显然成立，
（ii） 设n＝k时，3°式成立，
即
³1－（
）
则当n＝k＋1时，
³〔1－（）〕·（
）
＝1－（）－
＋（）
³1－（＋）即当n＝k＋1时，3°式也成立。
故对一切nÎN*，3°式都成立。
利用3°得，³1－（）＝1－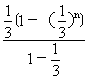
＝1－
>
故2°式成立，从而结论成立。