高考数学普通高等学校招生全国统一考试92
理科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至4页。全卷满分150分,考试时间120分钟。
考生注意事项:
1.答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。
2.答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.答第Ⅱ卷时,必须用0.5毫米墨水签字笔在答题卡上书写。在试题卷上作答无效。
4.考试结束,监考人员将试题卷和答题卡一并收回。
参考公式:
如果时间A、B互斥,那么![]()
如果时间A、B相互独立,那么![]()
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]()
球的表面积公式![]() ,其中R表示球的半径
,其中R表示球的半径
球的体积公式![]() ,其中R表示球的半径
,其中R表示球的半径
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)、复数![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)、设集合![]() ,
,![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(3)、若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(4)、设![]() ,已知命题
,已知命题![]() ;命题
;命题![]() ,则
,则![]() 是
是![]() 成立的
成立的
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
![]()
![]()
![]()
(5)、函数![]() 的反函数是
的反函数是
![]() ,
, ![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
A.![]() B.
B.![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
C.![]() D.
D.![]()
![]() ,
, ![]()
![]() ,
, ![]()
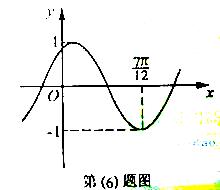 (6)、将函数
(6)、将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
A.![]()
B.![]()
C.![]()
D.![]()
(7)、若曲线![]() 的一条切线
的一条切线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的方程为
的方程为
A.![]()
B.![]()
C.![]()
D.![]()
(8)、设![]() ,对于函数
,对于函数![]() ,下列结论正确的是
,下列结论正确的是
A.有最大值而无最小值
B.有最小值而无最大值
C.有最大值且有最小值
D.既无最大值又无最小值
(9)、表面积为![]() 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
![]() ,
,
(10)、如果实数![]() 满足条件
满足条件 ![]() , 那么
, 那么![]() 的最大值为
的最大值为
![]() ,
,
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(11)、如果![]() 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于![]() 的三个内角的正弦值,则
的三个内角的正弦值,则
A.![]() 和
和![]() 都是锐角三角形
都是锐角三角形
B.![]() 和
和![]() 都是钝角三角形
都是钝角三角形
C.![]() 是钝角三角形,
是钝角三角形,![]() 是锐角三角形
是锐角三角形
D.![]() 是锐角三角形,
是锐角三角形,![]() 是钝角三角形
是钝角三角形
(12)、在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
高等学校招生全国统一考试
理科数学
第Ⅱ卷(非选择题 共90分)
注意事项:
请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效。
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在答题卡的相应位置。
(13)、设常数![]() ,
,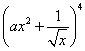 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则![]() __________。
__________。
(14)、在![]() 中,
中,![]() ,M为BC的中点,则
,M为BC的中点,则![]() _______。(用
_______。(用![]() 表示)
表示)
 (15)、函数
(15)、函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() _______________。
_______________。
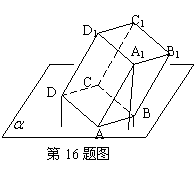
(16)、多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面![]() 内,其余顶点在
内,其余顶点在![]() 的同侧,正方体上与顶点A相邻的三个顶点到
的同侧,正方体上与顶点A相邻的三个顶点到![]() 的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面
的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面![]() 的距离可能是:
的距离可能是:
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为________________________。(写出所有正确结论的编号)
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤
(17)、(本大题满分12分)
已知![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求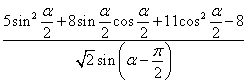 的值。
的值。
(18)、(本大题满分12分)
在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用![]() 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出![]() 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求![]() 的数学期望
的数学期望![]() 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)

(19)、(本大题满分12分)
如图,P是边长为1的正六边形ABCDEF所在平面外一点,![]() ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明![]() ⊥
⊥![]() ;
;
(Ⅱ)求面![]() 与面
与面![]() 所成二面角的大小。
所成二面角的大小。
(20)、(本大题满分12分)
已知函数![]() 在R上有定义,对任何实数
在R上有定义,对任何实数![]() 和任何实数
和任何实数![]() ,都有
,都有![]()
(Ⅰ)证明![]() ;
;
![]()
![]()
![]() ,
,
(Ⅱ)证明![]() 其中
其中![]() 和
和![]() 均为常数;
均为常数;
![]()
![]() ,
,
(Ⅲ)当(Ⅱ)中的![]() 时,设
时,设![]() ,讨论
,讨论![]() 在
在![]() 内的单调性并求极值。
内的单调性并求极值。
(21)、(本大题满分12分)
数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]()
(Ⅰ)写出![]() 与
与![]() 的递推关系式
的递推关系式![]() ,并求
,并求![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
(22)、(本大题满分14分)
 如图,F为双曲线C:
如图,F为双曲线C:![]() 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,![]() 为坐标原点。已知四边形
为坐标原点。已知四边形![]() 为平行四边形,
为平行四边形,![]() 。
。
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若
时,经过焦点F且品行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。
普通高等学校招生全国统一考试
理科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至4页。全卷满分150分,考试时间120分钟。
考生注意事项:
1.答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。
2.答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.答第Ⅱ卷时,必须用0.5毫米墨水签字笔在答题卡上书写。在试题卷上作答无效。
4.考试结束,监考人员将试题卷和答题卡一并收回。
参考公式:
如果时间A、B互斥,那么![]()
如果时间A、B相互独立,那么![]()
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]()
球的表面积公式![]() ,其中R表示球的半径
,其中R表示球的半径
球的体积公式![]() ,其中R表示球的半径
,其中R表示球的半径
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:![]() 故选A
故选A
(2)设集合![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:![]() ,
,![]() ,所以
,所以![]() ,故选B。
,故选B。
(3)若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:椭圆![]() 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线![]() 的焦点为(2,0),则
的焦点为(2,0),则![]() ,故选D。
,故选D。
(4)设![]() ,已知命题
,已知命题![]() ;命题
;命题![]() ,则
,则![]() 是
是![]() 成立的( )
成立的( )
A.必要不充分条件 B.充分不必要条件C.充分必要条件 D.既不充分也不必要条件
解:命题![]() 是命题
是命题![]() 等号成立的条件,故选B。
等号成立的条件,故选B。
(5)函数![]() 的反函数是( )
的反函数是( )
A.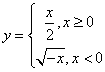 B.
B. C.
C.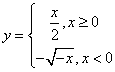 D.
D.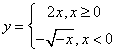
解:有关分段函数的反函数的求法,选C。
 (6)将函数
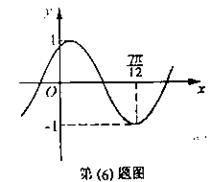
(6)将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解:将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象所对应的解析式为
平移,平移后的图象所对应的解析式为![]() ,由图象知,
,由图象知,![]() ,所以
,所以![]() ,因此选C。
,因此选C。
(7)若曲线![]() 的一条切线
的一条切线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:与直线![]() 垂直的直线
垂直的直线![]() 为
为![]() ,即
,即![]() 在某一点的导数为4,而
在某一点的导数为4,而![]() ,所以
,所以![]() 在(1,1)处导数为4,此点的切线为
在(1,1)处导数为4,此点的切线为![]() ,故选A
,故选A
(8)设![]() ,对于函数
,对于函数![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
解:令![]() ,则函数
,则函数![]() 的值域为函数
的值域为函数![]() 的值域,又
的值域,又![]() ,所以
,所以![]() 是一个减函减,故选B。
是一个减函减,故选B。
(9)表面积为![]() 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:此正八面体是每个面的边长均为![]() 的正三角形,所以由
的正三角形,所以由![]() 知,
知,![]() ,则此球的直径为
,则此球的直径为![]() ,故选A。
,故选A。
(10)如果实数![]() 满足条件
满足条件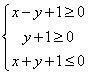 ,那么
,那么![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:当直线![]() 过点(0,-1)时,
过点(0,-1)时,![]() 最大,故选B。
最大,故选B。
(11)如果![]() 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于![]() 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A.![]() 和
和![]() 都是锐角三角形 B.
都是锐角三角形 B.![]() 和
和![]() 都是钝角三角形
都是钝角三角形
C.![]() 是钝角三角形,
是钝角三角形,![]() 是锐角三角形
是锐角三角形
D.![]() 是锐角三角形,
是锐角三角形,![]() 是钝角三角形
是钝角三角形
解:![]() 的三个内角的余弦值均大于0,则
的三个内角的余弦值均大于0,则![]() 是锐角三角形,若
是锐角三角形,若![]() 是锐角三角形,由
是锐角三角形,由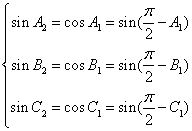 ,得
,得 ,那么,
,那么,![]() ,所以
,所以![]() 是钝角三角形。故选D。
是钝角三角形。故选D。
(12)在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:在正方体上任选3个顶点连成三角形可得![]() 个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得
个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得![]() ,所以选C。
,所以选C。
2006年普通高等学校招生全国统一考试(安徽卷)理科数学
第Ⅱ卷(非选择题 共90分)
注意事项:
请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效。
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在答题卡的相应位置。
(13)设常数![]() ,
,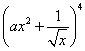 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则![]() _____。
_____。
解:![]() ,由
,由![]()
![]() ,所以
,所以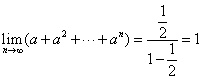 ,所以为1。
,所以为1。
(14)在![]() 中,
中,![]() ,M为BC的中点,则
,M为BC的中点,则![]() _______。(用
_______。(用![]() 表示)
表示)
解:![]() ,
,![]() ,所以
,所以![]() 。
。
(15)函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() __________。
__________。
 解:由
解:由![]() 得
得![]() ,所以
,所以![]() ,则
,则![]() 。
。
(16)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面![]() 内,其余顶点在
内,其余顶点在![]() 的同侧,正方体上与顶点A相邻的三个顶点到
的同侧,正方体上与顶点A相邻的三个顶点到![]() 的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面
的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面![]() 的距离可能是:
的距离可能是:
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为______________。(写出所有正确结论的编号)
解:如图,B、D、A1到平面![]() 的距离分别为1、2、4,则D、A1的中点到平面
的距离分别为1、2、4,则D、A1的中点到平面![]() 的距离为3,所以D1到平面
的距离为3,所以D1到平面![]() 的距离为6;B、A1的中点到平面
的距离为6;B、A1的中点到平面![]() 的距离为
的距离为![]() ,所以B1到平面
,所以B1到平面![]() 的距离为5;则D、B的中点到平面
的距离为5;则D、B的中点到平面![]() 的距离为
的距离为![]() ,所以C到平面
,所以C到平面![]() 的距离为3;C、A1的中点到平面
的距离为3;C、A1的中点到平面![]() 的距离为
的距离为![]() ,所以C1到平面
,所以C1到平面![]() 的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤
(17)(本大题满分12分)已知![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求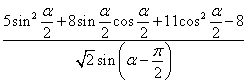 的值。
的值。
解:(Ⅰ)由![]() 得
得![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() 为所求。
为所求。
(Ⅱ)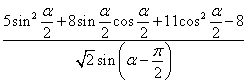 =
=
=![]() =
=![]() =
=![]() 。
。
(18)(本大题满分12分)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用![]() 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出![]() 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求![]() 的数学期望
的数学期望![]() 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)
解:(Ⅰ)
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| P |
|
|
|
|
|
|
|
|
|
 (Ⅱ)
(Ⅱ)![]()
(19)(本大题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点,![]() ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明![]() ⊥
⊥![]() ;
;
(Ⅱ)求面![]() 与面
与面![]() 所成二面角的大小。
所成二面角的大小。
解:(Ⅰ)在正六边形ABCDEF中,![]() 为等腰三角形,
为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;又∵正六边形ABCDEF的边长为1,∴![]() ,
,![]() ,
,![]() 。
。
过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,所以![]() 为所求二面角平面角。
为所求二面角平面角。
在![]() 中,OH=
中,OH=![]() ,
,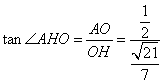 =
=![]() 。
。
在![]() 中,
中, ;
;
而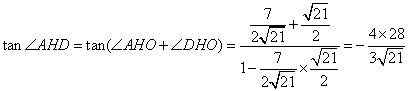
(Ⅱ)以O为坐标原点,建立空间直角坐标系,P(0,0,1),A(0,![]() ,0),B(
,0),B(![]() ,0,0),D(0,2,0),∴
,0,0),D(0,2,0),∴![]() ,
,![]() ,
,![]()
设平面PAB的法向量为![]() ,则
,则![]() ,
,![]() ,得
,得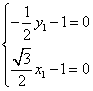 ,
,![]() ;
;
设平面PDB的法向量为![]() ,则
,则![]() ,
,![]() ,得
,得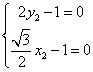 ,
,![]() ;
;

(20)(本大题满分12分)已知函数![]() 在R上有定义,对任何实数
在R上有定义,对任何实数![]() 和任何实数
和任何实数![]() ,都有
,都有![]()
(Ⅰ)证明![]() ;(Ⅱ)证明
;(Ⅱ)证明![]() 其中
其中![]() 和
和![]() 均为常数;
均为常数;
(Ⅲ)当(Ⅱ)中的![]() 时,设
时,设![]() ,讨论
,讨论![]() 在
在![]() 内的单调性并求极值。
内的单调性并求极值。
证明(Ⅰ)令![]() ,则
,则![]() ,∵
,∵![]() ,∴
,∴![]() 。
。
(Ⅱ)①令![]() ,∵
,∵![]() ,∴
,∴![]() ,则
,则![]() 。
。
假设![]() 时,
时,![]()
![]() ,则
,则![]() ,而
,而![]() ,∴
,∴![]() ,即
,即![]() 成立。
成立。
②令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,![]()
假设![]() 时,
时,![]()
![]() ,则
,则![]() ,而
,而![]() ,∴
,∴![]() ,即
,即![]() 成立。∴
成立。∴![]() 成立。
成立。
(Ⅲ)当![]() 时,
时,![]() ,
,![]()
令![]() ,得
,得![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() 是单调递减函数;
是单调递减函数;
当![]() 时,
时,![]() ,∴
,∴![]() 是单调递增函数;
是单调递增函数;
所以当![]() 时,函数
时,函数![]() 在
在![]() 内取得极小值,极小值为
内取得极小值,极小值为![]()
(21)(本大题满分12分)数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]()
(Ⅰ)写出![]() 与
与![]() 的递推关系式
的递推关系式![]() ,并求
,并求![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
解:由![]()
![]() 得:
得:![]() ,即
,即![]() ,所以
,所以![]() ,对
,对![]() 成立。
成立。
由![]() ,
,![]() ,…,
,…,![]() 相加得:
相加得:![]() ,又
,又![]() ,所以
,所以![]() ,当
,当![]() 时,也成立。
时,也成立。
(Ⅱ)由![]() ,得
,得![]() 。
。
而![]() ,
,
![]() ,
,
![]()
(22)(本大题满分14分)如图,F为双曲线C:![]() 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,![]() 为坐标原点。已知四边形
为坐标原点。已知四边形![]() 为平行四边形,
为平行四边形,![]() 。
。
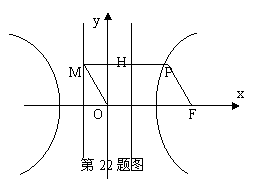 (Ⅰ)写出双曲线C的离心率
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。
解:∵四边形![]() 是
是![]() ,∴
,∴![]() ,作双曲线的右准线交PM于H,则
,作双曲线的右准线交PM于H,则![]() ,又
,又 ,
,![]() 。
。
(Ⅱ)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,双曲线为
,双曲线为![]() 四边形
四边形![]() 是菱形,所以直线OP的斜率为
是菱形,所以直线OP的斜率为![]() ,则直线AB的方程为
,则直线AB的方程为![]() ,代入到双曲线方程得:
,代入到双曲线方程得:![]() ,
,
又![]() ,由
,由![]() 得:
得:![]() ,解得
,解得![]() ,则
,则![]() ,所以
,所以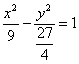 为所求。
为所求。