高考数学普通高等学校招生全国统一考试65
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)题两部分,满分150分.考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上。用2B铅笔将答题卡试卷类型(A)填涂在答题卡上。在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号,并用2B铅笔将相应的试室号、座位号信息点涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
( 1 ) 若集合![]() ,则M∩N
,则M∩N![]() ( )
( )
A.{3} B.{0} C.{0,2} D.{0,3}
【答案】B
解: ∵由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
∴M∩N![]() ,故选B.
,故选B.
( 2 ) 若![]() ,其中a、b∈R,i是虚数单位,则
,其中a、b∈R,i是虚数单位,则![]() = ( )
= ( )
A.0 B.2 C.![]() D.5
D.5
【答案】D
解: ∵ ![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,故选D.
,故选D.
( 3 ) ![]() = ( )
= ( )
A.![]() B.0 C.
B.0 C.![]() D.
D.![]()
【答案】A
解: ![]() ,故选A.
,故选A.
 ( 4 ) 已知高为3的直棱锥
( 4 ) 已知高为3的直棱锥![]() 的底面是边长为1的正三角形
的底面是边长为1的正三角形
(如图1所示),则三棱锥![]() 的体积为
( )
的体积为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
解:∵ ![]()
∴![]() .
.
故选D.
( 5 ) 若焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,则m=( )
,则m=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
解: ∵![]() ,∴
,∴![]() ,
,
∵ ![]() ,∴
,∴![]() ,
,
∴![]() ,故选B.
,故选B.
( 6 )函数![]() 是减函数的区间为 ( )
是减函数的区间为 ( )
A.![]() B.
B.![]() C.
C.![]() D.(0,2)
D.(0,2)
【答案】D
解: ∵![]()
![]() ,故选D.
,故选D.
( 7 ) 给出下列关于互不相同的直线![]() 、
、![]() 、
、![]() 和平面
和平面![]() 、
、![]() ,的四个命题:
,的四个命题:
①若![]() ,点
,点![]() ,则
,则![]() 与
与![]() 不共面;
不共面;
②若m、l是异面直线, ![]() , 且
, 且![]() ,则
,则![]() ;
;
③若![]() ,
, ![]() ,则
,则![]() ;
;
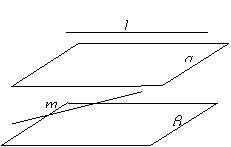 ④若
④若![]() 点
点![]() ,
,![]() ,则
,则![]() .
.
其中为假命题的是
A.① B.② C.③ D.④
【答案】C
解:③是假命题,如右图所示
满足![]() ,
, ![]() ,
,
但 ![]() ,故选C.
,故选C.
( 8 ) 先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子
朝上的面的点数分别为X、Y,则![]() 的概率为 ( )
的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
解:满足![]() 的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以
的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以![]() ,故选C.
,故选C.
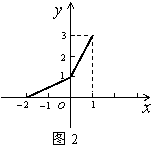 |
( 9 ) 在同一平面直角坐标系中,函数![]() 和
和![]() 的图像
的图像
关于直线![]() 对称.现将
对称.现将![]() 图像沿x轴向左平移2个单位,
图像沿x轴向左平移2个单位,
再沿y轴向上平移1个单位,所得的图像是由两条线段组成的折线
(如图2所示),则函数![]() 的表达式为
的表达式为
A.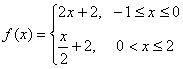 B.
B.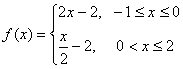
C.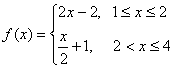 D.
D.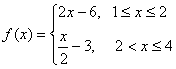
【答案】A
解:将图象沿y轴向下平移1个单位,再沿![]() 轴向右平移2个单位得下图A,从而可以得到
轴向右平移2个单位得下图A,从而可以得到![]() 的图象,故
的图象,故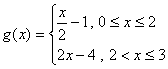 ,
,
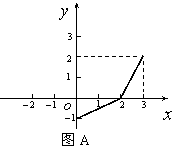 ∵函数
∵函数![]() 和
和![]() 的图像关于直线
的图像关于直线![]() 对称,
对称,
∴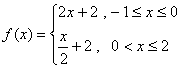 ,故选A.
,故选A.
(也可以用特殊点检验获得答案)
(10)已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .若
.若![]() ,则
,则![]()
A.![]() B.3 C.4 D.5
B.3 C.4 D.5
【答案】B
解法一:特殊值法,当![]() 时,
时,![]()
由此可推测![]() ,故选B.
,故选B.
解法二:∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 是以(
是以(![]() )为首项,以
)为首项,以![]() 为公比6的等比数列,
为公比6的等比数列,
令![]() ,则
,则![]()
![]() …
…![]()
![]() …
…![]()
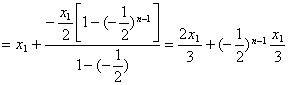
∴![]() ,∴
,∴![]() ,故选B.
,故选B.
解法三:∵![]() ,∴
,∴![]() ,
,
∴其特征方程为![]() ,
,
解得 ![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,以下同解法二.
,以下同解法二.
第二部分 非选择题(共100分)
二.填空题:本大题共4小题目,每小题5分,共20分.
(11)函数![]() 的定义域是
.
的定义域是
.
【答案】![]()
解:使![]() 有意义,则
有意义,则![]() ,
,
∴ ![]() ,∴
,∴![]() ,
,
∴![]() 的定义域是
的定义域是![]() .
.
(12)已知向量![]() ,
,![]() ,且
,且![]() ,则
,则![]() .
.
【答案】4
解:∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(13)已知![]() 的展开式中
的展开式中![]() 的系数与
的系数与![]() 的展开式中
的展开式中![]() 的系数相等,则
的系数相等,则![]()
.
【答案】![]()
解:![]() 的通项为
的通项为![]() ,
,![]() ,
,
∴![]() 的展开式中
的展开式中![]() 的系数是
的系数是![]() ,
,
![]() 的通项为
的通项为![]() ,
,![]() ,
,
∴![]() 的展开式中
的展开式中![]() 的系数是
的系数是![]()
∴ ![]() ,
,![]() .
.
(14)设平面内有![]() 条直线
条直线![]() ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用![]() 表示这
表示这![]() 条直线交点的个数,则
条直线交点的个数,则![]() =____________;当
=____________;当![]() 时,
时,![]() .(用
.(用![]() 表示)
表示)
【答案】5,![]()
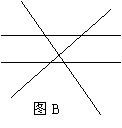 解:由图B可得
解:由图B可得![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,
![]() ,可推得
,可推得
∵n每增加1,则交点增加![]() 个,
个,
∴![]()
![]()
![]() .
.
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
( 15 )(本小题满分12分)
化简![]() 并求函数
并求函数![]() 的值域和最小正周期.
的值域和最小正周期.
【答案】
解: ![]()
![]()
![]()
![]()
![]()
∴ ![]() ,
,![]() ,
,
∴![]() 的值域是
的值域是![]() ,最小正周期是
,最小正周期是![]() .
.
 ( 16 ) (本小题共14分)
( 16 ) (本小题共14分)
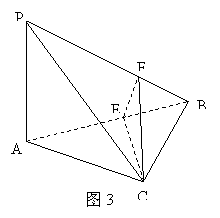
如图3所示,在四面体![]() 中,已知
中,已知![]() ,
,
![]() .
.![]() 是线段
是线段![]() 上一点,
上一点,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
【答案】
(Ⅰ)证明:在![]() 中, ∵
中, ∵![]()
∴![]()
∴△PAC是以∠PAC为直角的直角三角形,
同理可证,△PAB是以∠PAB为直角的直角三角形,
△PCB是以∠PCB为直角的直角三角形.
在![]() 中,∵
中,∵![]()
∴![]() ∴
∴![]()
又∵![]()
∴![]()
(II)
解法一:由(I)知PB⊥CE,PA⊥平面ABC
∴AB是PB在平面ABC上的射影,故AB⊥CE
∴CE⊥平面PAB,而EF![]() 平面PAB,
平面PAB,
∴EF⊥EC,
故∠FEB是二面角B—CE—F的平面角,
∵![]()
∴![]() ,
,
∴二面角B—CE—F的大小为![]() .
.
解法二:如图,以C点的原点,CB、CA为x、y轴,
建立空间直角坐标系C-xyz,则
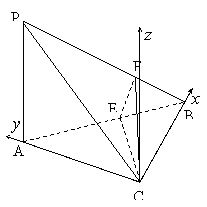
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() 为平面ABC的法向量,
为平面ABC的法向量,
![]() 为平面ABC的法向量,
为平面ABC的法向量,
∴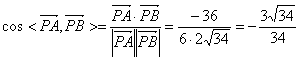 ,
,
∴二面角B—CE—F的大小为![]() .
.
|
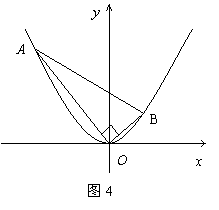 在平面直角坐标系
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 上异于坐标原点
上异于坐标原点![]() 的两不同动点A、B满足
的两不同动点A、B满足![]() (如图4所示)
(如图4所示)
(Ⅰ)求![]() 得重心
得重心![]() (即三角形三条中线的交点)
(即三角形三条中线的交点)
的轨迹方程;
(Ⅱ)![]() 的面积是否存在最小值?若存在,请求出
的面积是否存在最小值?若存在,请求出
最小值;若不存在,请说明理由.
【答案】
解法一:
(Ⅰ)∵直线![]() 的斜率显然存在,∴设直线
的斜率显然存在,∴设直线![]() 的方程为
的方程为![]() ,
,
![]() ,依题意得
,依题意得
![]() ,①
,①
∴![]() ,②
,② ![]() ③
③
∵![]() ,∴
,∴![]() ,即
,即 ![]() ,④
,④
由③④得,![]() ,∴
,∴![]()
∴设直线![]() 的方程为
的方程为![]()
∴①可化为 ![]() ,∴
,∴![]() ⑤,
⑤,
设![]() 的重心G为
的重心G为![]() ,则
,则
![]() ⑥ ,
⑥ , ![]() ⑦,
⑦,
由⑥⑦得 ![]() ,即
,即![]() ,这就是
,这就是![]() 得重心
得重心![]() 的轨迹方程.
的轨迹方程.
(Ⅱ)由弦长公式得![]()
把②⑤代入上式,得 ![]() ,
,
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
∴ ![]() ,
,
∴ 当![]() ,
,![]() 有最小值,
有最小值,
∴![]() 的面积存在最小值,最小值是
的面积存在最小值,最小值是![]() .
.
解法二:
(Ⅰ)∵ AO⊥BO, 直线![]() ,
,![]() 的斜率显然存在,
的斜率显然存在,
∴设AO、BO的直线方程分别为![]() ,
,![]() ,
,
设![]() ,
,![]() ,依题意可得
,依题意可得
由![]() 得
得 ![]() ,由
,由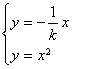 得
得 ![]() ,
,
设![]() 的重心G为
的重心G为![]() ,则
,则
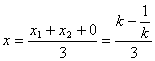 ① ,
① , 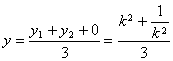 ②,
②,
由①②可得,![]() ,即为所求的轨迹方程.
,即为所求的轨迹方程.
(Ⅱ)由(Ⅰ)得,![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 有最小值,
有最小值,
∴![]() 的面积存在最小值,最小值是
的面积存在最小值,最小值是![]() .
.
解法三:(I)设△AOB的重心为G(x , y) ,A(x1, y1),B(x2 , y2 ),则
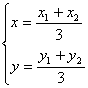 …(1)
…(1)
不过∵OA⊥OB ,
∴![]() ,即
,即![]() , …(2)
, …(2)
又点A,B在抛物线上,有![]() ,
,
代入(2)化简得![]() ,
,
∴![]() ,
,
∴所以重心为G的轨迹方程为![]() ,
,
(II)![]() ,
,
由(I)得![]() ,
,
当且仅当![]() 即
即![]() 时,等号成立,
时,等号成立,
所以△AOB的面积存在最小值,存在时求最小值1 .
( 18 ) (本小题共12分)
箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为![]() .现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次.以
.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次.以![]() 表示取球结束时已取到白球的次数.
表示取球结束时已取到白球的次数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)求![]() 的数学期望.
的数学期望.
【答案】
解:(Ⅰ)取出黄球的概率是![]() ,取出白球的概率是
,取出白球的概率是![]() ,则
,则
![]() ,
, ![]() ,
, ![]() ,
,
……, ![]() ,
, ![]() ,
,
∴![]() 的分布列是
的分布列是
|
| 0 | 1 | 2 | … |
|
|
|
|
|
|
| … |
|
|
(Ⅱ)
![]() …
…![]() ①
①
![]() …
…![]() ②
②
①—②得
![]() …
…![]()
∴ ![]()
∴![]() 的数学期望是
的数学期望是![]() .
.
( 19 ) (本小题共14分)
设函数![]() 在
在![]() 上满足
上满足![]() ,
,![]() ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有![]() .
.
(Ⅰ)试判断函数![]() 的奇偶性;
的奇偶性;
(Ⅱ)试求方程![]() 在闭区间
在闭区间![]() 上的根的个数,并证明你的结论.
上的根的个数,并证明你的结论.
【答案】
解:(Ⅰ)∵![]() ,
,
∴![]()
即 ![]() ,
,
∵在[0,7]上,只有![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 是非奇非偶函数.
是非奇非偶函数.
(Ⅱ)由![]() ,令
,令![]() ,得
,得 ![]() ,
,
由![]() ,令
,令![]() ,得
,得 ![]() ,
,
∴![]() ,
,
∴![]() 是以10为周期的周期函数,
是以10为周期的周期函数,
由![]() 得,
得,![]() 的图象关于
的图象关于![]() 对称,
对称,
∴在[0,11]上,只有![]() ,
,
∴10是![]() 的最小正周期,
的最小正周期,
∵在[0,10]上,只有![]() ,
,
∴在每一个最小正周期内![]() 只有两个根,
只有两个根,
∴在闭区间![]() 上的根的个数是
上的根的个数是![]() .
.
 ( 20 ) (本小题共14分)
( 20 ) (本小题共14分)
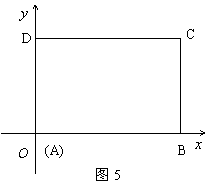
在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1,![]() 、
、![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() 点与坐标原点重合(如图5所示).将矩形折叠,使
点与坐标原点重合(如图5所示).将矩形折叠,使![]() 点落在线段
点落在线段![]() 上.
上.
(Ⅰ)若折痕所在直线的斜率为![]() ,试写出折痕所在直线的方程;
,试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.
【答案】
解:(Ⅰ)( i ) 当![]() 时,此时A点与D点重合, 折痕所在的直线方程
时,此时A点与D点重合, 折痕所在的直线方程![]() ,
,
( ii ) 当![]() 时,设A点落在线段
时,设A点落在线段![]() 上的点
上的点![]() ,
,
![]() ,则直线
,则直线![]() 的斜率
的斜率![]() ,
,
∵![]()
∴![]() ,∴
,∴![]() ,∴
,∴![]()
又∵折痕所在的直线与![]() 的交点坐标(线段
的交点坐标(线段![]() 的中点)
的中点)
为![]() ,
,
∴折痕所在的直线方程![]() ,即
,即![]() ,
,
由( i ) ( ii )得折痕所在的直线方程为:![]()
![]()
(Ⅱ)折痕所在的直线与坐标轴的交点坐标为![]()
由(Ⅰ)知,![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
设折痕长度为d,所在直线的倾斜角为![]() ,
,
( i ) 当![]() 时,此时A点与D点重合, 折痕的长为2 ;
时,此时A点与D点重合, 折痕的长为2 ;
( ii )当![]() 时,
时,
设![]() ,
,![]() ,
,
![]() 时,l与线段AB相交,此时
时,l与线段AB相交,此时![]() ,
,
![]() 时,l与线段BC相交,此时
时,l与线段BC相交,此时![]() ,
,
![]() 时,l与线段AD相交,此时
时,l与线段AD相交,此时![]() ,
,
![]() 时,l与线段DC相交,此时
时,l与线段DC相交,此时![]() ,
,
∴将k所在的分为3个子区间:
①当![]() 时,折痕所在的直线l与线段DC、AB相交,
时,折痕所在的直线l与线段DC、AB相交,
折痕的长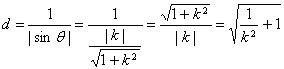 ,
,
∴![]() ,
,
②当![]() 时,折痕所在的直线l与线段AD、AB相交,
时,折痕所在的直线l与线段AD、AB相交,
![]()
![]()
令![]() ,即
,即![]() ,即
,即![]() ,
,
即 ![]() ,
,
∵![]() ,∴解得
,∴解得![]()
令![]() , 解得
, 解得 ![]() ,
,
故当![]() 时,
时,![]() 是减函数,当
是减函数,当![]() 时,
时,![]() 是增函数,
是增函数,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() ,
,
![]() ,
,
∴当![]() 时,
时, ![]() ,
,
③当![]() 时,折痕所在的直线l与线段AD、BC相交,
时,折痕所在的直线l与线段AD、BC相交,
折痕的长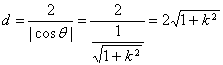 ,
,
∴![]() ,即
,即![]() ,
,
综上所述得,当![]() 时,折痕的长有最大值,为
时,折痕的长有最大值,为![]() .
.