高考数学普通高等学校招生全国统一考试38
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。第I卷1至2页。第II卷3至9页。共150分。考试时间120分钟。
第I卷(选择题 共40分)
注意事项:
1. 答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
3. 考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
三角函数的积化和差公式
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
![]()
其中c’,c分别表示上、下底面周长,![]() 表示斜高或母线长
表示斜高或母线长
球体的表面积公式![]()
其中R表示球的半径
一. 选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设全集是实数集R,![]() ,
,![]() ,则
,则![]() 等于
等于
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
(2)满足条件![]() 的复数z在复平面上对应点的轨迹是
的复数z在复平面上对应点的轨迹是
(A) 一条直线 (B) 两条直线 (C) 圆 (D) 椭圆
(3)设m、n是两条不同的直线,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是
(A) ①和② (B) ②和③ (C) ③和④ (D) ①和④
(4)如图,在正方体![]() 中,P是侧面
中,P是侧面![]() 内一动点,若P到直线BC与直线
内一动点,若P到直线BC与直线![]() 的距离相等,则动点P的轨迹所在的曲线是
的距离相等,则动点P的轨迹所在的曲线是
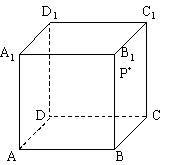
(A) 直线 (B) 圆 (C) 双曲线 (D) 抛物线
(5)函数![]() 在区间[1,2]上存在反函数的充分必要条件是
在区间[1,2]上存在反函数的充分必要条件是
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(6)已知a、b、c满足![]() ,且
,且![]() ,那么下列选项中一定成立的是
,那么下列选项中一定成立的是
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(7)从长度分别为1,2,3,4,5的五条线段中,任取三条的不同取法共有n种。在这些取法中,以取出的三条线段为边可组成的钝角三角形的个数为m,则![]() 等于
等于
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(8)函数![]() ,其中P、M为实数集R的两个非空子集,又规定
,其中P、M为实数集R的两个非空子集,又规定![]() ,
,![]() ,给出下列四个判断:
,给出下列四个判断:
①若![]() ,则
,则![]()
②若![]() ,则
,则![]()
③若![]() ,则
,则![]()
④若![]() ,则
,则![]()
其中正确判断有
(A) 1个 (B) 2个 (C) 3个 (D) 4个
第II卷(非选择题 共110分)
二. 填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上。
(9)函数![]() 的最小正周期是___________
的最小正周期是___________
(10)方程![]() 的解是___________________
的解是___________________
(11)某地球仪上北纬![]() 纬线的长度为
纬线的长度为![]() ,该地球仪的半径是__________cm,表面积是______________cm2
,该地球仪的半径是__________cm,表面积是______________cm2
(12)曲线C:![]() (
(![]() 为参数)的普通方程是__________,如果曲线C与直线
为参数)的普通方程是__________,如果曲线C与直线![]() 有公共点,那么实数a的取值范围是_______________--
有公共点,那么实数a的取值范围是_______________--
(13)在函数![]() 中,若a,b,c成等比数列且
中,若a,b,c成等比数列且![]() ,则
,则![]() 有最______________值(填“大”或“小”),且该值为______________
有最______________值(填“大”或“小”),且该值为______________
(14)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为5,那么
,公和为5,那么![]() 的值为______________,这个数列的前n项和
的值为______________,这个数列的前n项和![]() 的计算公式为________________
的计算公式为________________
三. 解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
(15)(本小题满分13分)
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值和
的值和![]() 的面积.
的面积.
(16)(本小题满分14分)
如图,在正三棱柱![]() 中,AB=3,
中,AB=3,![]() ,M为
,M为![]() 的中点,P是BC上一点,且由P沿棱柱侧面经过棱
的中点,P是BC上一点,且由P沿棱柱侧面经过棱![]() 到M的最短路线长为
到M的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为N,求:
的交点为N,求:
(I)该三棱柱的侧面展开图的对角线长
(II)PC和NC的长
(III)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)
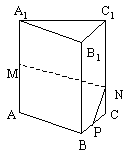
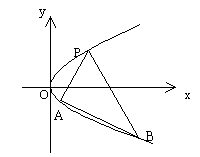
(17)(本小题满分14分)
如图,过抛物线![]() 上一定点P(
上一定点P(![]() )(
)(![]() ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A(![]() ),B(
),B(![]() )
)
(I)求该抛物线上纵坐标为![]() 的点到其焦点F的距离
的点到其焦点F的距离
(II)当PA与PB的斜率存在且倾斜角互补时,求![]() 的值,并证明直线AB的斜率是非零常数
的值,并证明直线AB的斜率是非零常数
(18)(本小题满分14分)
函数![]() 是定义在[0,1]上的增函数,满足
是定义在[0,1]上的增函数,满足![]() 且
且![]() ,在每个区间
,在每个区间![]() (
(![]() 1,2……)上,
1,2……)上,![]() 的图象都是斜率为同一常数k的直线的一部分。
的图象都是斜率为同一常数k的直线的一部分。
(I)求![]() 及
及![]() ,
,![]() 的值,并归纳出
的值,并归纳出![]() 的表达式
的表达式
(II)设直线![]() ,
,![]() ,x轴及
,x轴及![]() 的图象围成的矩形的面积为
的图象围成的矩形的面积为![]() (
(![]() 1,2……),记
1,2……),记![]() ,求
,求![]() 的表达式,并写出其定义域和最小值.
的表达式,并写出其定义域和最小值.
(19)(本小题满分12分)
某段城铁线路上依次有A、B、C三站,AB=15km,BC=3km,在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度![]() 匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差。
匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差。
(I)分别写出列车在B、C两站的运行误差
(II)若要求列车在B,C两站的运行误差之和不超过2分钟,求![]() 的取值范围.
的取值范围.
(20)(本小题满分13分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275。现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差![]() 与所有可能的其他选择相比是最小的,
与所有可能的其他选择相比是最小的,![]() 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为![]() ;如此继续构成第三组(余差为
;如此继续构成第三组(余差为![]() )、第四组(余差为
)、第四组(余差为![]() )、……,直至第N组(余差为
)、……,直至第N组(余差为![]() )把这些数全部分完为止。
)把这些数全部分完为止。
(I)判断![]() 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n<N)组后,指出余下的每个数与![]() 的大小关系,并证明
的大小关系,并证明![]()
(III)对任何满足条件T的有限个正数,证明:![]()
普通高等学校招生全国统一考试
参考答案
一. 选择题:本大题主要考查基本知识和基本运算。每小题5分,满分40分。
(1)A (2)C (3)A (4)D
(5)D (6)C (7)B (8)B
二. 填空题:本大题主要考查基本知识和基本运算。每小题5分,满分30分。
(9)![]() (10)
(10)![]()
(11)![]()
![]()
(12)![]()
![]()
(13)大 -3
(14)3 当n为偶数时,![]() ;当n为奇数时,
;当n为奇数时,![]()
三. 解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
(15)本小题主要考查三角恒等变形、三角形面积公式等基本知识,考查运算能力。满分13分。
解法一:
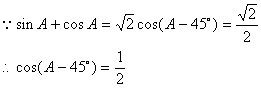
又![]()
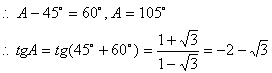
![]()
![]()
解法二:
![]() (1)
(1)
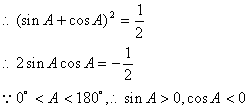
![]()
![]() (2)
(2)
(1)+(2)得:![]()
(1)-(2)得:![]()
![]()
(以下同解法一)
(16)本小题主要考查直线与平面的位置关系、棱柱等基本知识,考查空间想象能力、逻辑思维能力和运算能力。满分14分。
解:(I)正三棱柱![]() 的侧面展开图是一个长为9,宽为4的矩形,其对角线长为
的侧面展开图是一个长为9,宽为4的矩形,其对角线长为![]()
(II)如图1,将侧面![]() 绕棱
绕棱![]() 旋转
旋转![]() 使其与侧成
使其与侧成![]() 在同一平面上,点P运动到点
在同一平面上,点P运动到点![]() 的位置,连接
的位置,连接![]() ,则
,则![]() 就是由点P沿棱柱侧面经过棱
就是由点P沿棱柱侧面经过棱![]() 到点M的最短路线
到点M的最短路线
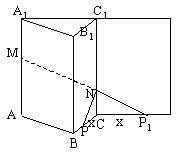
设![]() ,则
,则![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]()
求得![]()
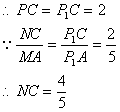
(III)如图2,连结![]() ,则
,则![]() 就是平面NMP与平面ABC的交线,作
就是平面NMP与平面ABC的交线,作![]() 于H,又
于H,又![]() 平面ABC,连结CH,由三垂线定理得,
平面ABC,连结CH,由三垂线定理得,![]()
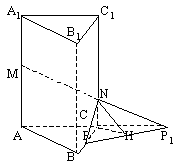
![]() 就是平面NMP与平面ABC所成二面角的平面角(锐角)
就是平面NMP与平面ABC所成二面角的平面角(锐角)
在![]() 中,
中,![]()
![]()
在![]() 中,
中,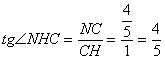
故平面NMP与平面ABC所成二面角(锐角)的大小为![]()
(17)本小题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力。满分14分
解:(I)当![]() 时,
时,![]()
又抛物线![]() 的准线方程为
的准线方程为![]()
由抛物线定义得,所求距离为![]()

(2)设直线PA的斜率为![]() ,直线PB的斜率为
,直线PB的斜率为![]()
由![]() ,
,![]()
相减得![]()
故![]()
同理可得![]()
由PA,PB倾斜角互补知![]()
即![]()
所以![]()
故![]()
设直线AB的斜率为![]()
由![]() ,
,![]()
相减得![]()
所以![]()
将![]() 代入得
代入得
![]() ,所以
,所以![]() 是非零常数
是非零常数
(18)本小题主要考查函数、数列等基本知识,考查分析问题和解决问题的能力。满分14分。
解:(I)由![]() ,得
,得![]()
由![]() 及
及![]() ,得
,得![]()
同理,![]()
归纳得![]()
(II)当![]() 时
时
![]()
![]()
![]()
所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列
的等比数列
所以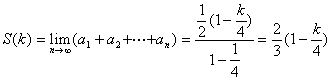
![]() 的定义域为
的定义域为![]() 1,当
1,当![]() 时取得最小值
时取得最小值![]()
(19)本小题主要考查解不等式等基本知识,考查应用数学知识分析问题和解决问题的能力。满分12分。
解:(I)列车在B,C两站的运行误差(单位:分钟)分别是
![]() 和
和![]()
(II)由于列车在B,C两站的运行误差之和不超过2分钟,所以
![]() (*)
(*)
当![]() 时,(*)式变形为
时,(*)式变形为![]()
解得![]()
当![]() 时,(*)式变形为
时,(*)式变形为![]()
解得![]()
当![]() 时,(*)式变形为
时,(*)式变形为![]()
解得![]()
综上所述,![]() 的取值范围是[39,
的取值范围是[39,![]() ]
]
(20)本小题主要考查不等式的证明等基本知识,考查逻辑思维能力、分析问题和解决问题的能力。满分13分。
解:(I)![]() 。除第N组外的每组至少含有
。除第N组外的每组至少含有![]() 个数
个数
(II)当第n组形成后,因为![]() ,所以还有数没分完,这时余下的每个数必大于余差
,所以还有数没分完,这时余下的每个数必大于余差![]() ,余下数之和也大于第n组的余差
,余下数之和也大于第n组的余差![]() ,即
,即
![]()
由此可得![]()
因为![]() ,所以
,所以![]()
(III)用反证法证明结论,假设![]() ,即第11组形成后,还有数没分完,由(I)和(II)可知,余下的每个数都大于第11组的余差
,即第11组形成后,还有数没分完,由(I)和(II)可知,余下的每个数都大于第11组的余差![]() ,且
,且![]()
故余下的每个数![]() (*)
(*)
因为第11组数中至少含有3个数,所以第11组数之和大于![]()
此时第11组的余差![]()
这与(*)式中![]() 矛盾,所以
矛盾,所以![]()