高考数学高等学校招生全国统一考试32

高考数学高等学校招生全国统一考试32

文科数学（必修+选修Ⅰ）

本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 共150分. 考试时间120分钟.

第I卷　

参考公式：

　　　 如果事件A、B互斥，那么

P（A+B）=P（A）+P（B）

　　　 如果事件A、B相互独立，那么

P（A·B）=P（A）·P（B）

　　　 如果事件A在一次试验中发生的概率是P，那么

n次独立重复试验中恰好发生k次的概率

P_n(k)=CP^k(1－P)^n－k

一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有

一项是符合题目要求的.

（1）设集合U={1，2，3，4，5}，集合M={0，3，5}，N={1，4，5}，则M∩（　_U N）=

　　　 （A）{5}　　　　　　　　 （B）{0，3}　　　　　　（C）{0，2，3，5} （D） {0，1，3，4，5}

（2）函数的反函数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 （A）　　　　　　　　　　　　　 （B）

　　　 （C）　　　　　　　　　　　　　（D）

（3）正三棱柱侧面的一条对角线长为2，且与底面成45°角，则此三棱柱的体积为　　　　　　 （A）　　 （B） 　　　 （C）　　　　　　　 （D）

（4） 函数在处的导数等于　　　　　　　　　　　　　　　　　　　　　　　　　　 （A）1　 （B）2　 （C）3　 （D）4

（5）为了得到函数的图象，可以把函数的图象　　　　　　　　　　　　　 （A）向左平移3个单位长度　　　 （B）向右平移3个单位长度

　　　 （C）向左平移1个单位长度　　　　　　　　　 （D）向右平移1个单位长度

（6）等差数列中，，则此数列前20项和等于

　　　 （A）160　　　　　　　　 （B）180　　　　　　　　 （C）200　　　　　　　　 （D）220

（7）已知函数的图象有公共点A，且点A的横坐标为2，则　　　　　　　（A）　　 （B） （C）　　　　　　　　　　　　　　　　（D）

（8）已知圆C的半径为2，圆心在轴的正半轴上，直线与圆C相切，则圆C的方程为　　　　　　　　　　　

（A）　　　　　　　　　　 （B）

　　　 （C）　　　　　　　　　　 （D）

（9） 从5位男教师和4位女教师中选出3位教师，派到3个班担任班主任（每班1位班任），要求这3位班主任中男、女教师都要有，则不同的选派方案共有　　

（A）210种　　　　 （B）420种　　　　　　 （C）630种　　　　　　 （D）840种

（10）函数的最小值等于　　　　　　　　　　　　　　　　　　（A）－3　　　 （B）－2　　　 （C）－1　　 （D）－

（11）已知球的表面积为20，球面上有A、B、C三点.如果AB=AC=BC=2，则球心到平面ABC的距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（A）1　　　　　　　　　 （B）　　　　　　　　（C）　　　　　　　　（D）2

（12）△ABC中，a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列，

　　　 ∠B=30°，△ABC的面积为，那么b=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（A）　　　 （B）　　　 （C）　　　　　（D）

第Ⅱ卷

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

（13）展开式中的系数为　　　 　　　 .

（14）已知函数的最小正周期为3，则A=　　　　　 .

（15）向量a、b满足（a－b）·（2a+b）=－4，且a=2，b=4，则a与b夹角的余弦值等于

　　  　　　　　 .

（16）设满足约束条件：

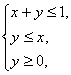
则的最大值是　　　 　　　　 .

三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.

（17）（本小题满分12分）

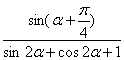已知α为第二象限角，且 sinα=求的值.

（18）（本小题满分12分）

　　　 已知数列{}为等比数列，

（Ⅰ）求数列{}的通项公式；

（Ⅱ）设是数列{}的前项和，证明

（19）（本小题满分12分）

　　　 已知直线为曲线在点（1，0）处的切线，为该曲线的另一条切线，且

（Ⅰ）求直线的方程；

（Ⅱ）求由直线、和轴所围成的三角形的面积.

（20）（本小题满分12分）

　　　 某同学参加科普知识竞赛，需回答3个问题.竞赛规则规定：答对第一、二、三问题分别得100分、100分、200分，答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6，且各题答对与否相互之间没有影响.

（Ⅰ）求这名同学得300分的概率；

（Ⅱ）求这名同学至少得300分的概率.

（21）（本小题满分12分）

　　　 如图，四棱锥P—ABCD中，底面ABCD 为矩形，AB=8，AD=4，侧面PAD为等边三角形，并且与底面所成二面角为60°.

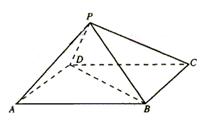
（Ⅰ）求四棱锥P—ABCD的体积；

（Ⅱ）证明PA⊥BD.

（22）（本小题满分14分）

　　　 双曲线的焦距为2c，直线过点（a，0）和（0，b），且点（1，0）到直线的距离与点（－1，0）到直线的距离之和求双曲线的离心率e的取值范围.

普通高等学校招生全国统一考试

文科数学（必修+选修Ⅱ）参考答案

一、选择题

（1）B　　 （2）C　　　 （3）A　　　（4）D　　  （5）D　　　（6）B

（7）A　　 （8）D　　　 （9）B　　　（10）C　　 （11）A　　 （12） B

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

（13）28　　　　（14）　 　　　（15）　　　　 （16）2

三、解答题

（17）本小题主要考查同角三角函数的基本关系式，二倍角公式以及三角函数式的恒等变形等基础知识和基本技能.满分12分.

解：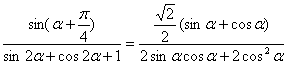

　　　　　　　　　　 

　 当为第二象限角，且时

　 ，

所以=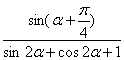

（18）本小题主要考查等比数列的概念、前n项和公式等基础知识，考查学生综合运用基础知识进行运算的能力.满分12分.

解：（I）设等比数列{a_n}的公比为q，则a₂=a₁q, a₅=a₁q⁴.

　　　　　　　　 a₁q=6,

依题意，得方程组 a₁q⁴=162.

解此方程组，得a₁=2, q=3.

故数列{a_n}的通项公式为a_n=2·3^n－1.

（II）

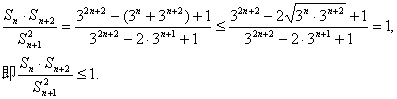
（19）本小题主要考查导数的几何意义，两条直线垂直的性质以及分析问题和综合运算能力.满分12分.

解：y′=2x+1.

直线l₁的方程为y=3x－3.

设直线l₂过曲线y=x²+x－2上 的点B（b, b²+b－2）,则l₂的方程为y=(2b+1)x－b²－2

因为l₁⊥l₂，则有2b+1=

所以直线l₂的方程为

（II）解方程组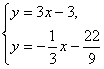　得

所以直线l₁和l₂的交点的坐标为

l₁、l₂与x轴交点的坐标分别为（1，0）、.

所以所求三角形的面积

（20）本小题主要考查相互独立事件同时发生的概率和互斥事件有一个发生的概率的计算方法，应用概率知识解决实际问题的能力.满分12分.

　 解：记“这名同学答对第i个问题”为事件，则

　　  P（A₁）=0.8，P（A₂）=0.7，P（A₃）=0.6.

（Ⅰ）这名同学得300分的概率

　　  P₁=P（A₁A₃）+P（A₂A₃）

　　　  =P（A₁）P（）P（A₃）+P（）P（A₂）P（A₃）

　　　　=0.8×0.3×0.6+0.2×0.7×0.6

　　  　=0.228.

（Ⅱ）这名同学至少得300分的概率

　　 P₂=P₁+P（A₁A₂A₃）

　　  =0.228+P（A₁）P（A₂）P（A₃）

　　  =0.228+0.8×0.7×0.6

　　  =0.564.

（21）本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析

问题能力.满分12分.

　 解：（Ⅰ）如图1，取AD的中点E，连结PE，则PE⊥AD.

作PO⊥平面在ABCD，垂足为O，连结OE.

根据三垂线定理的逆定理得OE⊥AD，

所以∠PEO为侧面PAD与底面所成的二面角的平面角，

由已知条件可知∠PEO=60°，PE=6，

所以PO=3，四棱锥P—ABCD的体积

V_P—ABCD=

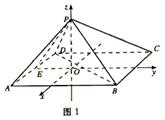
（Ⅱ）解法一：如图1，以O为原点建立空间直角坐标系.通过计算可得

P（0，0，3），A（2，－3，0），B（2，5，0），D（－2，－3，0）

所以

因为 所以PA⊥BD.

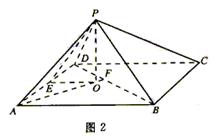
解法二：如图2，连结AO，延长AO交BD于点F.能过计算可得EO=3，AE=2，

又知AD=4，AB=8，

得

所以　Rt△AEO∽Rt△BAD.

　　　　得∠EAO=∠ABD.

　　　　所以∠EAO+∠ADF=90°

　 所以　AF⊥BD.

　 因为　直线AF为直线PA在平面ABCD 内的身影，所以PA⊥BD.

（22）本小题主要考查点到直线距离公式，双曲线的基本性质以及综合运算能力.满分12分.

　解：直线的方程为，即　

由点到直线的距离公式，且，得到点（1，0）到直线的距离

，

同理得到点（－1，0）到直线的距离

由　 即　 

于是得　

解不等式，得　 由于所以的取值范围是