高考全国普通高等学校招生统一考试数学试卷2
一、填空题：
1、
已知集合
，集合
。若
，则实数
。
2、
已知圆
的圆心是点P，则点P到直线
的距离是 
。
3、
若函数
的反函数的图象过点
，则
。
4、
计算：
。
5、
若复数
同时满足
，
（
为虚数单位），则
。
6、
如果
，且
是第四象限的角，那么
。
7、
已知椭圆中心在原点，一个焦点为
，且长轴长是短轴长的2倍，则该椭圆的标准方程是
8、
在极坐标系中，
是极点。设点
，
，则
的面积是 
。
9、
两部不同的长篇小说各由第一、二、三、四卷组成，每卷1本，共8本。将它们任意地排成一排，左边4本恰好都属于同一部小说的概率是 
（结果用分数表示）。
10、如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”。在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是
。
11、若曲线
与直线
没有公共点，则
、
分别应满足的条件是 
。
12、三个同学对问题“关于
的不等式
在
上恒成立，求实数
的取值范围”提出各自的解题思路。
甲说：“只须不等式左边的最小值不小于右边的最大值”。
乙说：“把不等式变形为左边含变量
的函数，右边仅含常数，求函数的最值”。
丙说：“把不等式两边看成关于的函数，作出函数图象”。
参考上述解题思路，你认为他们所讨论的问题的正确结论，即的取值范围是 
。
二、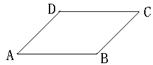
选择题：
13、如图，在平行四边形ABCD中，下列结论中错误的是 （ C ）
（A）
（B）
（C）
（D）
14、若空间中有四个点，则“这四个点中有三点在同一条直线上”是“这四个点在同一个平面上”的（ A ）
（A）充分非必要条件 （B）必要非充分条件
（C）充分必要条件 （D）既非充分又非必要条件
15、若关于的不等式
的解集是
，则对任意实常数，总有（ A ）
（A）
（B）
（C）
（D）
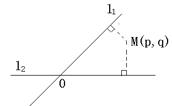16、如图，平面中两条直线
和
相交于点。对于平面上任意一点，若
、
分别是到直线和的距离，则称有序非负实数对
是点的“距离坐标”。已知常数
，给出下列三个命题：
①若
，则“距离坐标”为
的点有且仅有1个。
②若
，且
，则“距离坐标”为的点有且仅有2个。
③若
，则“距离坐标”为的点有且仅有4个。
上述命题中，正确命题的个数是 （ D ）
（A）0 （B）1 （C）2 （D）3
三、解答题：
17、求函数
的值域和最小正周期。
解：
，
，
。
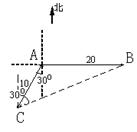
18、如图，当甲船位于
处时获悉，在其正东方向相距
海里的
处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西
，相距
海里
处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往处救援（角度精确到
）？
解：
∴乙船应朝北偏东约
的方向沿直线前往处救援。
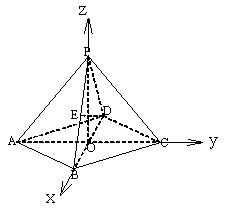
19、在四棱锥
中，底面是边长为
的菱形，
，对角线
与
相交于点，
⊥平面
，
与平面所成的角为
．
（1）求四棱锥的体积；
（2）若
是的中点，求异面直线
与
所成角的大小（结果用反三角函数值表示）．
解：（1）底面是边长为的菱形，
⊥平面，与平面所成的角为
，
∴
。
（2）建系如图，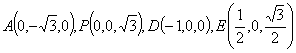
，
，
，
，
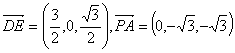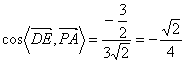∴异面直线与所成角的大小为
。
20、在平面直角坐标系O
中，直线
与抛物线
相交于、两点。
（1）求证：“如果直线过点
，那么
＝
”是真命题；
（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由。
解：（1）如果直线
轴，则
如果直线与轴不垂直，设直线的方程为
，
∴
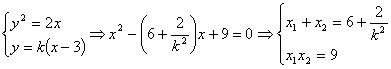
综上，得“如果直线过点，那么＝”是真命题。
（2）（1）中命题的逆命题：在平面直角坐标系O中，直线与抛物线
＝2相交于、两点。如果 ＝，那么直线必过点。
∵设直线与轴的交点坐标为
，则直线方程为
，把它代入得
由
，即直线必过点
。
∴（1）中命题的逆命题是假命题。
21．已知有穷数列
共有2项（整数≥2），首项
＝2．设该数列的前
项和为
，且
＝
＋2（＝1，2，┅，2－1），其中常数＞1．
（1）求证：数列是等比数列；
（2）若＝2
，数列
满足＝
（＝1，2，┅，2），求数列的通项公式；
（3）若（2）中的数列满足不等式
－
＋
－＋┅＋
－＋
－≤4，求的值．
解：（1）
，则
，两式相减，得
，
（又
）
∴数列是首项为、公比为的等比数列。
（2）＝
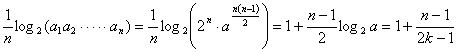，（＝1，2，┅，2）。
（3）由（2）知，数列是首项为、公差为
的等差数列。
又
，∴
时，
；
时，
。
∴－＋－＋┅＋－＋－
。
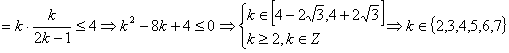22．已知函数＝＋
有如下性质：如果常数＞0，那么该函数在
0，
上是减函数，在
，＋∞
上是增函数．
（1）如果函数＝＋
（＞0）的值域为6，＋∞，求的值；
（2）研究函数＝
＋
（常数
＞0）在定义域内的单调性，并说明理由；
（3）对函数＝＋和＝＋
（常数＞0）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必证明），并求函数
＝
＋
（是正整数）在区间[，2]上的最大值和最小值（可利用你的研究结论）．
解：（1）易知，
时，
。
（2）＝＋是偶函数。易知，该函数在
上是减函数，在
上是增函数；则该函数在
上是减函数，在
上是增函数。
（3）推广：函数
，当为奇数时，
，是减函数；
，是增函数。
，是增函数；
，是减函数。
当为偶数时，，是减函数；，是增函数。
，是减函数；，是增函数。
＝＋
当
时，
。
∴
，是减函数；
，是增函数。
∵
∴函数＝＋在区间[，2]上的最大值为
，最小值为
。