高考试题数学(理工类)

高考试题数学(理工类)

第Ⅰ卷 (选择题 共60分)

　一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．＝(　　)

(A) 2　　 (B) 4　　 (C) 　　　 (D)0

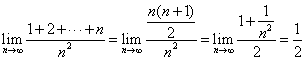解：,选(C)

2．点(1，－1)到直线x－y＋1＝0的距离是(　　)

(A)　　　 (B) 　　 (C) 　　(D)

解：点(1,-1)到直线x-y+1=0的距离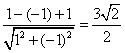d=,选(D)

3．设f(x)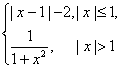＝，则f[f()]＝(　　)

(A) 　　 (B)　　  (C)－　　 (D)

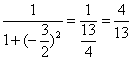解：f[f()]=f[-1-2]=f[-]=,选(B)

4．在复平面内，复数＋(1＋i)²对应的点位于(　　)

(A) 第一象限　　 (B) 第二象限　　(C) 第三象限　 (D)第四象限

解：+(1＋i)^{2=-2+2i=+2i,故}在复平面内，复数＋(1＋i)²对应的点为(^{,2i),故选(B)}

5．在(1－x)⁵＋(1－x)⁶＋(1－x)⁷＋(1－x)⁸的展开式中，含x³的项的系数是(　　)

(A) 74　 (B) 121　　(C) －74　　(D) －121

解：(1－x)⁵＋(1－x)⁶＋(1－x)⁷＋(1－x)^{8=,(1-x)5中x4的系数为,-(1-x)9中x4的系数为-,-126+5=-121,故选(D)}

6．设、 为两个不同的平面，l、m为两条不同的直线，且l，m，有如下的两个命题：

①若∥，则l∥m；②若l⊥m，则⊥．

那么

(A) ①是真命题，②是假命题　　(B) ①是假命题，②是真命题

(C) ①②都是真命题　　　　　  (D) ①②都是假命题

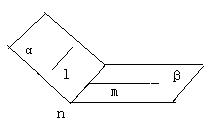解：命题②有反例,如

图中平面α∩平面β=直线n,l

且l∥n,m⊥n,则m⊥l,显然平面α不垂直平面β

故②是假命题；命题①显然也是假命题,

因此本题选(D)

7．设集合A＝{(x，y)x，y，1－x－y是三角形的三边长}，则A所表示的平面区域(不含边界的阴影部分)是(　  )

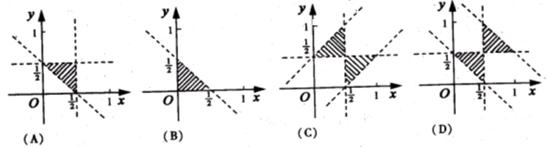
解：由题意可知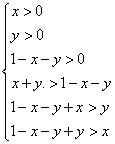得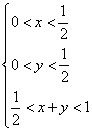由此可知A所表示的平面区域(不含边界的阴影部分)是(A )

8．已知k＜－4，则函数y＝cos2x＋k(cosx－1)的最小值是(　  )

(A) 1　　 (B) －1　  (C) 2k＋1　　 (D) －2k＋1

解：y＝cos2x＋k(cosx－1)=2cos²x+ k(cosx－1)-1,当cosx=1时,y=1,当cosx≠1时,cosx-1<0,则y>2cos²x-4(cosx－1)-1=2(cosx-1)²+1≥1,故y的最小值为1,选(A)

9．设f(n)＝2n＋1(n∈N)，P＝{1，2，3，4，5}，Q＝{3，4，5，6，7}，记＝{n∈Nf(n)∈P}，＝{n∈Nf(n)∈Q}，则(∩)∪(∩)＝(　　)

(A) {0，3}　 (B){1，2}　  (C) (3，4，5)　(D){1，2，6，7}

解：={0,1,2},={n∈Nn≥2},={1,2,3},={n∈Nn=0或n≥4},

故∩={0},∩={3},得(∩)∪(∩)＝{0,3},选(A)

10．已知向量≠，＝1，对任意t∈R，恒有－t≥－，则

(A) ⊥　　  (B) ⊥(－)　(C) ⊥(－)　(D) (＋)⊥(－)

解：由－t≥－得－t²≥－²展开并整理得,得,即,选(C)

第Ⅱ卷 (非选择题 共100分)

二、填空题：本大题共4小题，每小题4分，共16分。把答案填在答题卡的相应位置。 

11．函数y＝(x∈R，且x≠－2)的反函数是_________．

解：由y＝(x∈R，且x≠－2),得x=(y∈R,y≠1),所以函数y＝(x∈R，且x≠－2)的反函数是f^-1=(x∈R,x≠1).

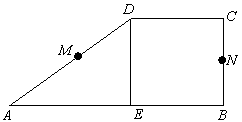12．设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E(如图)．现将△ADE沿DE折起，使二面角A－DE－B为45°，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小等于_________．

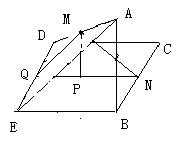解：如左图,在平面AED内作MQ∥AE交ED于Q,则MQ⊥ED,且Q为ED的中点,连结QN,则NQ⊥ED且QN∥EB,QN=EB,∠MQN为二面角A－DE－B的平面角,

∴∠MQN=45°∵AB⊥平面BCDE,又∠AEB=∠MQN=45°,MQ=AE=EB,在平面MQN内作MP⊥BQ,得QP=MP=EB,故PB=QP=EB,故QMN是以∠QMN为直角的等腰三角形,即MN⊥QM,也即MN子AE所成角大小等于90°

13．过双曲线(a＞0，b＞0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点，以MN为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于_________．

解：由题意可得,即c²-a²=a²+ac,化成关于e的方程e²-e-2=0,解得e=2

12．从集合{O，P，Q，R，S}与{0，1，2，3，4，5，6，7，8，9}中各任取2个元素排成一排(字母和数字均不能重复)．每排中字母O，Q和数字0至多只能出现一个的不同排法种数是_________．(用数字作答)．

解：分三种情况：情况1.不含O、Q、0的排列：；情况2.O、Q中只含一个元素的排列：；情况3.只含元素0的排列：.综上符合题意的排法种数为

++=8424

三、解答题：本大题共6小题，每小题14分，共84分。解答应写出文字说明，证明过程或演算步骤。

　15．已知函数f(x)＝－sin²x＋sinxcosx．

　 (Ⅰ) 求f()的值；

　 (Ⅱ) 设∈(0，)，f()＝－，求sin的值．

解：(Ⅰ)∵

(Ⅱ)

,16sin²α-4sinα-11=0,解得sinα=

∵α∈(0,π),∴sinα>0,故sinα=

　16．已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x²＝2x．

　 (Ⅰ)求函数g(x)的解析式；

　 (Ⅱ)解不等式g(x)≥f(x)－x－1．

解：(Ⅰ)设函数y=f(x)的图象上任一点Q(x_q,y_q关于原点的对称点(x,y),

则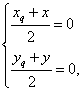即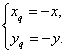∵点Qx_q,y_q)在函数f(x)的图象上,

∴-y=-x²+2x.,故g(x)=-x²+2x

(Ⅱ)由g(x)≥f(x)－x－1可得2x²-x-1≤0,当x≥1时,2x²-x+1≤0,此时不等式无解,

当x<1时,2x²+x-1≤0,∴-1≤x≤,因此,原不等式的解集为[-1,]

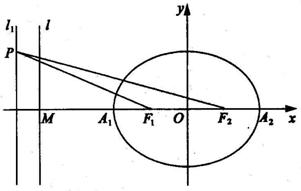
　 17．如图，已知椭圆的中心在坐标原点，焦点F₁，F₂在x轴上，长轴A₁A₂的长为4，左准线l与x轴的交点为M，MA₁∶A₁F₁＝2∶1．

　 (Ⅰ)求椭圆的方程；

　 (Ⅱ)若直线l₁：x＝m(m＞1)，P为l₁上的动点，使∠F₁PF₂最大的点P记为Q，求点Q的坐标(用m表示)．

　

解：(Ⅰ)设椭圆的方程为(a>0,b>0),半焦距为c,则MA₁=,A₁F₁=a-c
由题意,得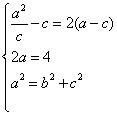∴a=2,b=,c=1.

故椭圆的方程为

(Ⅱ)设P(m,y_q),m>1,

当y_q=0时,∠F₁PF₂=0,当y_q≠0时,0<∠F₁PF₂<∠PF₁M<,

∴只需求tan∠F₁PF₂的最大值即可.

设直线PF₁的斜率k₁=,直线PF₂的斜率k₂=,

∴tan∠F₁PF₂=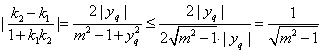

当且仅当时,∠F₁PF₂最大,∴Q(m,),m>1

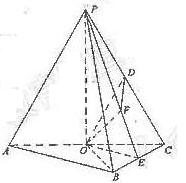
18．如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．

　

(Ⅰ)求证：OD∥平面PAB；

(Ⅱ)当k＝时，求直线PA与平面PBC所成角的大小；

　 (Ⅲ) 当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？

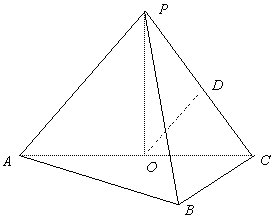
解：解法一

(Ⅰ)∵O、D分别为AC、PC的中点：∴OD∥PA,又AC平面PAB,∴OD∥平面PAB.

(Ⅱ)∵AB⊥BC,OA=OC,∴OA=OC=OB,又∵OP⊥平面ABC,∴PA=PB=PC.

取BC中点E,连结PE,则BC⊥平面POE,作OF⊥PE于F,连结DF,则OF⊥平面PBC

∴∠ODF是OD与平面PBC所成的角.

又OD∥PA,∴PA与平面PBC所成角的大小等于∠ODF.

在Rt△ODF中,sin∠ODF=,∴PA与平面PBC所成角为arcsin

(Ⅲ)由(Ⅱ)知,OF⊥平面PBC,∴F是O在平面PBC内的射影.

∵D是PC的中点,若F是△PBC的重心,则B、F、D三点共线,直线OB在平面PBC内的射影为直线BD,∵OB⊥PC.∴PC⊥BD,∴PB=BC,即k=1..反之,,当k=1时,三棱锥O-PBC为正三棱锥,∴O在平面PBC内的射影为△PBC的重心.

解法二：

∵OP⊥平面ABC,OA=OC,AB=BC,∴OA⊥OB,OA⊥OP,OB⊥OP.

以O为原点,射线OP为非负x轴,建立空间坐标系O-xyz如图),设AB=a,则A(a,0,0).

B(0, a,0),C(-a,0,0).设OP=h,则P(0,0,h).

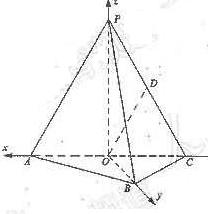
(Ⅰ)∵D为PC的中点,∴又∥,

∴OD∥平面PAB.

(Ⅱ)∵k=则PA=2a,∴h=∴可求得平面PBC的法向量

∴cos.

设PA与平面PBC所成角为θ,刚sinθ=cos()=.

∴PA与平面PBC所成的角为arcsin.

(Ⅲ)△PBC的重心G(),∴=().

∵OG⊥平面PBC,∴又∴,

∴h=,∴PA=,即k=1,反之,当k=1时,三棱锥O-PBC为正三棱锥.

∴O为平面PBC内的射影为△PBC的重心.

19．袋子A和B中装有若干个均匀的红球和白球，从A中摸出一个红球的概率是，从B中摸出一个红球的概率为p．

　(Ⅰ) 从A中有放回地摸球，每次摸出一个，有3次摸到红球即停止．(i)求恰好摸5次停止的概率；(ii)记5次之内(含5次)摸到红球的次数为，求随机变量的分布率及数学期望E．

　 (Ⅱ) 若A、B两个袋子中的球数之比为12，将A、B中的球装在一起后，从中摸出一个红球的概率是，求p的值．

解：(Ⅰ)().

(Ⅱ)随机变量ζ的取值为0、1、2、3.由n次独立重复试验概率公式P_n(k)=,得P(ζ=0)=,

P((ζ=1)=,

P((ζ=2)=,

P((ζ=3)=.

ζ	0	1	2	3
P

随机变量ζ的分布列是

　

 

ζ的数学期望是E(ζ)= ×0+×1+×2+×3=

(Ⅱ)设袋子A中有m个球,则袋子B中有2m个球,

由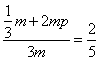,得p=.

20．设点(，0)，和抛物线：y＝x²＋a_n x＋b_n(n∈N*)，其中a_n＝－2－4n－，由以下方法得到：

　 x₁＝1，点P₂(x₂，2)在抛物线C₁：y＝x²＋a₁x＋b₁上，点A₁(x₁，0)到P₂的距离是A₁到C₁上点的最短距离，…，点在抛物线：y＝x²＋a_n x＋b_n上，点(，0)到的距离是 到 上点的最短距离．

　 (Ⅰ)求x₂及C₁的方程．

　 (Ⅱ)证明{}是等差数列．

解：(Ⅰ)由题意,得A(1,0),C₁：y=x²-7x+b₁.

设点P(x,y)是C₁上任意一点,则A₁P=

令f(x)=(x-1)²+(x²-7x+b₁)²,则由题意得,,

即又P₂(x₂,0)在C₁上,∴2=x₂² -7x₂+b₁

解得x₂=3,b₁=14.故C₁方程为y=x²-7x+14.

(Ⅱ)设P(x,y)是C₁上任意一点,则AnP=

令g(x)=(x-x_n)²+(x²+a_nx+bn)²,则,由题意得,,

即=0,

又∵,∴(x_n+1-x_n)+2ⁿ(2x_n+1+a_n)=0(n≥1),

即(1+2ⁿ⁺¹)x_n+1-x_n+2ⁿa_n=0,　 (*)

下面用数学归纳法证明x_n=2n-1.

①　　当n=1时,x₁=1,等式成立.

②　　假设当n=k时,等式成立,即x_k=2k-1.

则当n=k+1时,由(*)知(1+2^k+1)x_k+1-x_k+2^ka_k=0,　 (*)

又a_k=-2-4k-,∴.

即当n=k+1,时等式成立.

由①②知,等式对n∈N⁺成立,∴{x_n}是等差数列.