高考数学（理）模拟试题六
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请把答案填在题后的括号内．
1．
等于
（ ）
A．2 B．－2 C．
D．－
2．设条件P：
；条件
，那么p是q的什么条件 （ ）
A．充分非必要条件 B．必要非充分条件
C．充分且必要条件 D．非充分非必要条件
3．若O为平行四边形ABCD的中心，
等于 （ ）
A．
B．
C．
D．
4．
等于
（ ）
A．
B．
C．1 D．0
5．若a，b，c成等比数列，则函数
的图象与x轴的交点个数为 （ ）
A．0 B．1 C．2 D．不能确定
6．把函数
的图象向左平移m个单位（m>0）所得的图象关于y轴对称，则m的最小值是 （ ）
A．
B．
C．
D．
7．给出下列关于互不相同的直线
、
、
和平面
、
的四个命题：
①若
；
②若、是异面直线，
；
③若
；
④若
其中为假命题的是 （ ）
A．① B．② C．③ D．④
8．直线：
与直线：
的夹角为（ ）．
A．
B．
C．
D．
9．某校高三8个班级的师生为庆祝第二十一个教师节，每个班学生准备了一个节目，已排成节目单．开演前又增加了3个教师节目，其中2个独唱节目，1个朗诵节目．如果将这3个节目插入原节目单中，要求教师的节目不排在第一个和最后一个，并且2个独唱节目不连续演出，那么不同的插法有 （ ） A 294种 B 308种 C 378种 D 392种
10. 设动点A, B（不重合）在椭圆
上，椭圆的中心为O，且
，则O到弦AB的距离OH等于
（ ）
A．
B．
C．
D．
二、填空题：本大题共4小题，每小题5分，共20分．请把答案填在题中横线上．
11．
（
）展开式的常数项是
。
12．在条件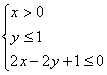
下，目标函数S=2x+y的最大值为
13．定义非空集合A的真子集的真子集为A的“孙集”，则集合{1,3,5,7,9}的“孙集”的个数有＿＿＿＿＿个．
14．设
是定义在R上的奇函数在(0，
)上单调递减，且
。给出下列四个结论：①
；②是以2为周期的函数；③在(，1)上单调递增；④
为奇函数。其中所有正确命题的序号是____________.
三、解答题：本大题共6小题，满分84分．解答应写出文字说明、证明过程或演算步骤．
15．已知向量a=（cosa，sina），b=（cosb，sinb），a−b=
．
（Ⅰ）求cos（a−b）的值；
（Ⅱ）若0<a<
，
<b<0，且sinb=
，求sina的值．
16．今有甲、乙两个篮球队进行比赛，规定两队中有一队胜4场则整个比赛宣告结束．假设甲、乙两队在每场比赛中获胜的概率都是
．并记需要比赛的场数为ξ．
（Ⅰ）求ξ大于5的概率；
（Ⅱ）求ξ的分布列与数学期望．
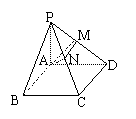17．如图，四棱锥P－ABCD的底面是正方形，PA⊥底面ABCD，PA＝AD＝2，点M、N分别在棱PD、PC上，且PC⊥平面AMN．
(1)求证：AM⊥PD；(2)求二面角P－AM－N的大小；
(3)求直线CD与平面AMN所成角的大小．
18． 已知函数
和g (x)的图象关于原点对称，且f
(x) = x2 +2x
（1）求函数g (x)的解析式；
（2）解不等式g (x)≥f (x)－x－1
19．．在面积为18的△ABC中，AB＝5，双曲线E过点A，且以B、C为焦点，已知·＝27，·＝54．
(1)建立适当的坐标系，求曲线E的方程；
(2)是否存在过点D(1，1)的直线L，使L与双曲线E交于不同的两点M、N，且
＋＝，如果存在，求出L的方程；如果不存在，说明理由．
20．已知
，各项为正的等差数列
满足
，又数列
的前项和是
。
（1）求数列的通项公式；
（2）求证：数列
是等比数列；
（3）设
，试问数列
有没有最大项？如果有，求出这个最大项，如果没有，
说明理由。