高考数学常用结论集锦
1.德摩根公式 ![]() .
.
2![]()
![]()
![]()
3. 若A={![]() },则A的子集有
},则A的子集有![]() 个,真子集有(
个,真子集有(![]() -1)个,非空真子集有(
-1)个,非空真子集有(![]() -2)个
-2)个
4.二次函数的解析式的三种形式 ①一般式![]() ;② 顶点式
;② 顶点式 ![]() ;③零点式
;③零点式![]() .
.
三次函数的解析式的三种形式①一般式![]()
②零点式![]()
5.设![]() 那么
那么
![]()
![]()
![]() 上是增函数;
上是增函数;
![]()
![]() 上是减函数.
上是减函数.
设函数![]() 在某个区间内可导,如果
在某个区间内可导,如果![]() ,则
,则![]() 为增函数;如果
为增函数;如果![]() ,则
,则![]() 为减函数.
为减函数.
6.函数![]() 的图象的对称性:
的图象的对称性:
①函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称![]()
![]()
②函数![]() 的图象关于直
的图象关于直![]() 对称
对称![]()
![]() .
.
③函数![]() 的图象关于点
的图象关于点![]() 对称
对称![]()
函数![]() 的图象关于点
的图象关于点![]() 对称
对称![]()
7.两个函数图象的对称性:
①函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() (即
(即![]() 轴)对称.
轴)对称.
②函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
特殊地: ![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
③函数![]() 的图象关于直线
的图象关于直线![]() 对称的解析式为
对称的解析式为![]()
④函数![]() 的图象关于点
的图象关于点![]() 对称的解析式为
对称的解析式为![]()
⑤函数![]() 和
和![]() 的图象关于直线y=x对称.
的图象关于直线y=x对称.
8.分数指数幂 ![]() (
(![]() ,且
,且![]() ).
).
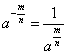 (
(![]() ,且
,且![]() ).
).
9.
![]() .
.
![]()
![]()
![]()
![]()
10.对数的换底公式 ![]() .推论
.推论 ![]() .
.
对数恒等式![]() (
(![]() )
)
11.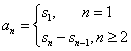 ( 数列
( 数列![]() 的前n项的和为
的前n项的和为![]() ).
).
12.等差数列![]() 的通项公式
的通项公式![]() ;
;
13.等差数列![]() 的变通项公式
的变通项公式![]()
对于等差数列![]() ,若
,若![]() ,(m,n,p,q为正整数)则
,(m,n,p,q为正整数)则![]() 。
。
14.若数列![]() 是等差数列,
是等差数列,![]() 是其前n项的和,
是其前n项的和,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 成等差数列。如下图所示:
成等差数列。如下图所示:
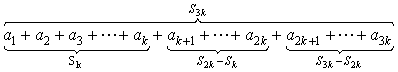
其前n项和公式 ![]()
![]()
![]() .
.
15.数列![]() 是等差数列
是等差数列![]()
![]() ,数列
,数列![]() 是等差数列
是等差数列![]()
![]() =
=![]()
16.设数列![]() 是等差数列,
是等差数列,![]() 是奇数项的和,
是奇数项的和,![]() 是偶数项项的和,
是偶数项项的和,![]() 是前n项的和,则有如下性质:
是前n项的和,则有如下性质:
1前n项的和![]()
2当n为偶数时,![]() ,其中d为公差;
,其中d为公差;
3当n为奇数时,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (其中
(其中![]() 是等差数列的中间一项)。
是等差数列的中间一项)。
17.若等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,等差数列
,等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,
,
则![]() 。
。
18.等比数列![]() 的通项公式
的通项公式![]() ;
;
等比数列![]() 的变通项公式
的变通项公式![]()
其前n项的和公式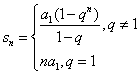 或
或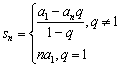 .
.
19. 对于等比数列![]() ,若
,若![]() (n,m,u,v为正整数),则
(n,m,u,v为正整数),则![]()
也就是:![]() 。如图所示:
。如图所示: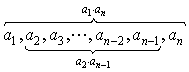
20. 数列![]() 是等比数列,
是等比数列,![]() 是其前n项的和,
是其前n项的和,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 成等比数列。如下图所示:
成等比数列。如下图所示:
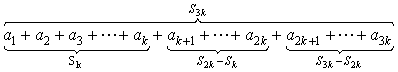
21. 同角三角函数的基本关系式 ![]() ,
,![]() =
=![]() ,
,![]()
. ![]()
22. 正弦、余弦的诱导公式
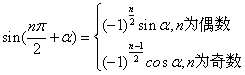
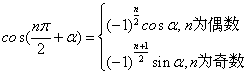
即:奇变偶不变,符号看象限,如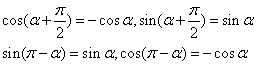
23. 和角与差角公式
![]() ;
;
![]() ;
;
![]() .
.
![]() (平方正弦公式);
(平方正弦公式);
![]() .
.
![]() =
=![]() (辅助角
(辅助角![]() 所在象限由点
所在象限由点![]() 的象限决定,
的象限决定,![]() ).
).
24. 二倍角公式 ![]() .
.
![]() .(升幂公式)
.(升幂公式)
![]() (降幂公式)
(降幂公式)
![]() .
.
25.万能公式:![]() ,
, ![]()
26.半角公式:![]()
27. 三函数的周期公式
函数![]() ,x∈R及函数
,x∈R及函数![]() ,x∈R(A,ω,
,x∈R(A,ω,![]() 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期![]() ;若ω未说明大于0,则
;若ω未说明大于0,则![]()
函数![]() ,
,![]() (A,ω,
(A,ω,![]() 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期![]() .
.
28. ![]() 的单调递增区间为
的单调递增区间为![]() 单调递减区间为
单调递减区间为
![]() ,对称轴为
,对称轴为![]() ,对称中心为
,对称中心为![]()
![]()
29. ![]() 的单调递增区间为
的单调递增区间为![]() 单调递减区间为
单调递减区间为![]() ,
,
对称轴为![]() ,对称中心为
,对称中心为![]()
![]()
30. ![]() 的单调递增区间为
的单调递增区间为![]() ,对称中心为
,对称中心为![]()
31. 正弦定理 ![]()
32. 余弦定理![]() ;
;![]() ;
; ![]() .
.
33.面积定理(1)![]() (
(![]() 分别表示a、b、c边上的高).
分别表示a、b、c边上的高).
(2)![]() .
.
(3)![]() =
=![]() (
(![]() 为
为![]() 的夹角)
的夹角)
34.三角形内角和定理 在△ABC中,有
![]()
![]() .
.
35.平面两点间的距离公式
![]() =
=![]()
![]() (A
(A![]() ,B
,B![]() ).
).
36.向量的平行与垂直 设a=![]() ,b=
,b=![]() ,且b
,且b![]() 0,则
0,则
a∥b![]() b=λa
b=λa ![]() .
.
a![]() b(a
b(a![]() 0)
0)![]() a·b=0
a·b=0![]() .
.
37.线段的定比分公式 设![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的分点,
的分点,![]() 是实数,且
是实数,且![]() ,则
,则
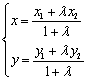
![]()
![]()
![]()
![]() (
(![]() ).
).
38.若![]() 则A,B,C共线的充要条件是x+y=1
则A,B,C共线的充要条件是x+y=1
39. 三角形的重心坐标公式 △ABC三个顶点的坐标分别为![]() 、
、![]() 、
、![]() ,则△ABC的重心的坐标是
,则△ABC的重心的坐标是![]() .
.
40.点的平移公式 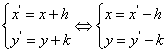
![]() (图形F上的任意一点P(x,y)在平移后图形
(图形F上的任意一点P(x,y)在平移后图形![]() 上的对应点为
上的对应点为![]() ,且
,且![]() 的坐标为
的坐标为![]() ).
).
41.常用不等式:
(1)![]()
![]()
![]() (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(2)![]()
![]()
![]() (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(3)![]()
(4)![]() 注意等号成立的条件
注意等号成立的条件
(5)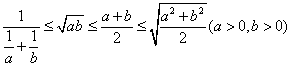
42.极值定理 已知![]() 都是正数,则有
都是正数,则有
(1)如果积![]() 是定值
是定值![]() ,那么当
,那么当![]() 时和
时和![]() 有最小值
有最小值![]() ;
;
(2)如果和![]() 是定值
是定值![]() ,那么当
,那么当![]() 时积
时积![]() 有最大值
有最大值![]() .
.
43.一元二次不等式![]()
![]() ,如果
,如果![]() 与
与![]() 同号,则其解集在两根之外;如果
同号,则其解集在两根之外;如果![]() 与
与![]() 异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
![]() ;
;
![]() .
.
44.含有绝对值的不等式 当a> 0时,有
![]() .
.
![]() 或
或![]() .
.
45.无理不等式(1)
(2)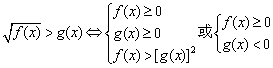 .
.
(3)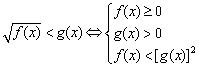 .
.
46.指数不等式与对数不等式 (1)当![]() 时,
时,
![]() ;
; 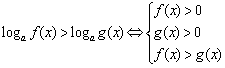 .
.
(2)当![]() 时,
时,
![]() ;
;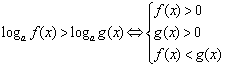
47.斜率公式 ![]() (
(![]() 、
、![]() )
)
直线的方向向量v=(a,b),则直线的斜率为![]() =
=![]()
48.直线方程的五种形式:
(1)点斜式 ![]() (直线
(直线![]() 过点
过点![]() ,且斜率为
,且斜率为![]() ).
).
(2)斜截式 ![]() (b为直线
(b为直线![]() 在y轴上的截距).
在y轴上的截距).
(3)两点式
![]() (
(![]() )(
)(![]() 、
、![]() (
(![]() )).
)).
(4)截距式![]()
(5)一般式
![]() (其中A、B不同时为0).
(其中A、B不同时为0).
49.两条直线的平行和垂直 (1)若![]() ,
,![]()
①![]() ;②
;②![]() .
.
(2)若![]() ,
,![]() ,
,
①![]() ;②
;②![]() ;
;
50.夹角公式 ![]() .(
.(![]() ,
,![]() ,
,![]() )
)
![]() (
(![]() ,
,![]() ,
,![]() ).
).
直线![]() 时,直线l1与l2的夹角是
时,直线l1与l2的夹角是![]() .
.
直线l1到l2的角是![]() (
(![]() ,
,![]() ,
,![]() )
)
51.点到直线的距离 ![]() (点
(点![]() ,直线
,直线![]() :
:![]() ).
).
52.两条平行线的间距离
![]() (直线
(直线![]()
![]() :
:![]() ).
).
53. 圆的四种方程
(1)圆的标准方程 ![]() .
.
(2)圆的一般方程 ![]() (
(![]() >0).
>0).
(3)圆的参数方程 ![]() .
.
(4)圆的直径式方程 ![]() (圆的直径的端点是
(圆的直径的端点是![]() 、
、![]() ).
).
54.圆中有关重要结论:
(1)若P(![]() ,
,![]() )是圆
)是圆![]() 上的点,则过点P(
上的点,则过点P(![]() ,
,![]() )的切线方程为
)的切线方程为![]()
(2)若P(![]() ,
,![]() )是圆
)是圆![]() 上的点,则过点P(
上的点,则过点P(![]() ,
,![]() )的切线方程为
)的切线方程为![]()
(3) 若P(![]() ,
,![]() )是圆
)是圆![]() 外一点,由P(
外一点,由P(![]() ,
,![]() )向圆引两条切线, 切点分别为A,B
)向圆引两条切线, 切点分别为A,B
则直线AB的方程为![]()
(4) 若P(![]() ,
,![]() )是圆
)是圆![]() 外一点, 由P(
外一点, 由P(![]() ,
,![]() )向圆引两条切线, 切点分别为A,B则直线AB的方程为
)向圆引两条切线, 切点分别为A,B则直线AB的方程为![]()
55.椭圆![]() 的参数方程是
的参数方程是![]() .
.
56.椭圆![]() 焦半径公式
焦半径公式 ![]() ,
,![]() .
.
56.椭圆![]() 的准线方程为
的准线方程为![]() ,椭圆
,椭圆![]() 的准线方程为
的准线方程为![]()
57.椭圆![]() 的通径(过焦点且垂直于对称轴的弦)长为
的通径(过焦点且垂直于对称轴的弦)长为![]()
58.P是椭圆![]() 上一点,F
上一点,F![]() ,F
,F![]() 是它的两个焦点,∠F
是它的两个焦点,∠F![]() P F
P F![]() =θ
=θ
则△P F![]() F
F![]() 的面积=
的面积=![]()
59.双曲线![]() 的准线方程为
的准线方程为![]()
双曲线![]() 的准线方程为
的准线方程为![]()
60. 双曲线![]() 的渐近线方程为
的渐近线方程为![]()
双曲线![]() 的的渐近线方程为
的的渐近线方程为![]()
61.P是双曲线![]() 上一点,F
上一点,F![]() ,F
,F![]() 是它的两个焦点,∠F
是它的两个焦点,∠F![]() P F
P F![]() =θ
=θ
则△P F![]() F
F![]() 的面积=
的面积=![]()
62.抛物线![]() 上的动点可设为P
上的动点可设为P![]() 或
或![]() P
P![]() ,其中
,其中 ![]() .
.
63. P(![]() ,
,![]() )是抛物线
)是抛物线![]() 上的一点,F是它的焦点,则PF=
上的一点,F是它的焦点,则PF=![]() +
+![]()
64. 抛物线![]() 的焦点弦长
的焦点弦长![]() ,其中
,其中![]() 是焦点弦与x轴的夹角
是焦点弦与x轴的夹角
65.直线与圆锥曲线相交的弦长公式 ![]() 或
或
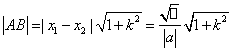 (弦端点A
(弦端点A![]() ,由方程
,由方程![]() 消去y得到
消去y得到![]() ,
,![]() ,
,![]() 为直线的斜率).
为直线的斜率).
若(弦端点A![]() 由方程
由方程![]() 消去x得到
消去x得到![]() ,
,![]() ,
,![]() 为直线的斜率).则
为直线的斜率).则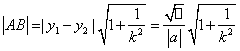
66.圆锥曲线![]() 关于点
关于点![]() 成中心对称的曲线是
成中心对称的曲线是![]() .
.
67.共线向量定理 对空间任意两个向量a、b(b≠0 ),a∥b![]() 存在实数λ使a=λb.
存在实数λ使a=λb.
68.对空间任一点O和不共线的三点A、B、C,满足![]() ,
,
则四点P、A、B、C是共面![]()
![]() .
.
69. 空间两个向量的夹角公式 cos〈a,b〉=![]() (a=
(a=![]() ,b=
,b=![]() ).
).
70.直线![]() 与平面所成角
与平面所成角![]() (
(![]() 为平面
为平面![]() 的法向量).
的法向量).
71.二面角![]() 的平面角
的平面角![]() 或
或![]() (
(![]() ,
,![]() 为平面
为平面![]() ,
,![]() 的法向量).
的法向量).
72.设AC是α内的任一条直线,且BC⊥AC,垂足为C,又设AO与AB所成的角为![]() ,AB与AC所成的角为
,AB与AC所成的角为![]() ,AO与AC所成的角为
,AO与AC所成的角为![]() .则
.则![]() .
.
73.若夹在平面角为![]() 的二面角间的线段与二面角的两个半平面所成的角是
的二面角间的线段与二面角的两个半平面所成的角是![]() ,
,![]() ,与二面角的棱所成的角是θ,则有
,与二面角的棱所成的角是θ,则有![]() ;
;
![]() (当且仅当
(当且仅当![]() 时等号成立).
时等号成立).
74.空间两点间的距离公式 若A![]() ,B
,B![]() ,则
,则
![]() =
=![]()
![]() .
.
75.点![]() 到直线
到直线![]() 距离
距离![]() (点
(点![]() 在直线
在直线![]() 上,直线
上,直线![]() 的方向向量a=
的方向向量a=![]() ,向量b=
,向量b=![]() ).
).
76.异面直线间的距离 ![]() (
(![]() 是两异面直线,其公垂向量为
是两异面直线,其公垂向量为![]() ,
,![]() 分别是
分别是![]() 上任一点,
上任一点,![]() 为
为![]() 间的距离).
间的距离).
77.点![]() 到平面
到平面![]() 的距离
的距离 ![]() (
(![]() 为平面
为平面![]() 的法向量,
的法向量,![]() 是经过面
是经过面![]() 的一条斜线,
的一条斜线,![]() ).
).
78. ![]()
![]()
(长度为![]() 的线段在三条两两互相垂直的直线上的射影长分别为
的线段在三条两两互相垂直的直线上的射影长分别为![]() ,夹角分别为
,夹角分别为![]() )(立几中长方体对角线长的公式是其特例).
)(立几中长方体对角线长的公式是其特例).
79. 面积射影定理 ![]()
(平面多边形及其射影的面积分别是![]() 、
、![]() ,它们所在平面所成锐二面角的为
,它们所在平面所成锐二面角的为![]() ).
).
80.球的半径是R,则其体积是![]() ,其表面积是
,其表面积是![]() .
.
81.![]()
82.分类计数原理(加法原理)![]() .
.
83.分步计数原理(乘法原理)![]() .
.
84.排列数公式 ![]() =
=![]() =
=![]() .(
.(![]() ,
,![]() ∈N*,且
∈N*,且![]() ).
).
85.排列恒等式 (1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ; (4)
; (4)![]() ;(5)
;(5)![]() .
.
86.组合数公式
![]() =
=![]() =
=![]() =
=![]() (
(![]() ,
,![]() ∈N*,且
∈N*,且![]() ).
).
87.组合数的两个性质(1) ![]() =
=![]() ;(2)
;(2) ![]() +
+![]() =
=![]()
88.组合恒等式(1)![]() ;(2)
;(2)![]() ;
;
(3)![]() ; (4)
; (4) ![]()
(5)![]() =
=![]() ;(5)
;(5)![]() .
.
89.排列数与组合数的关系是:![]() .
.
90.二项式定理 ![]() ;
;
二项展开式的通项公式:![]()
![]() .
.
91.等可能性事件的概率![]() .
.
92.互斥事件A,B分别发生的概率的和P(A+B)=P(A)+P(B).
93.![]() 个互斥事件分别发生的概率的和
个互斥事件分别发生的概率的和
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
94.独立事件A,B同时发生的概率P(A·B)= P(A)·P(B).
95.n个独立事件同时发生的概率 P(A1· A2·…· An)=P(A1)· P(A2)·…· P(An).
96.n次独立重复试验中某事件恰好发生k次的概率![]()
97.函数![]() 在点
在点![]() 处的导数是曲线
处的导数是曲线![]() 在
在![]() 处的切线的斜率
处的切线的斜率![]() ,相应的切线方程是
,相应的切线方程是![]() .
.
98.导数与函数的单调性的关系
㈠![]() 与
与![]() 为增函数的关系。
为增函数的关系。
![]() 能推出
能推出![]() 为增函数,但反之不一定。如函数
为增函数,但反之不一定。如函数![]() 在
在![]() 上单调递增,但
上单调递增,但![]() ,∴
,∴![]() 是
是![]() 为增函数的充分不必要条件。
为增函数的充分不必要条件。
㈡![]() 与
与![]() 为增函数的关系。
为增函数的关系。
![]() 为增函数,一定可以推出
为增函数,一定可以推出![]() ,但反之不一定,因为
,但反之不一定,因为![]() ,即为
,即为![]() 或
或![]() 。当函数在某个区间内恒有
。当函数在某个区间内恒有![]() ,则
,则![]() 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴![]() 是
是![]() 为增函数的必要不充分条件。
为增函数的必要不充分条件。
99.抽象函数的性质所对应的一些具体特殊函数模型:
①![]()
![]() 正比例函数
正比例函数![]()
②![]() ;
;![]()
![]()
![]()
③![]() ;
;![]()
![]()
![]() ;
;
100.n个数据![]() ,则它们的平均数为
,则它们的平均数为![]() ,
,
方差![]() =
=![]()