普通高等学校招生全国统一考试数学分类汇编
第十二章《极限》
一、选择题(共3题)
1.(湖南卷)数列{![]() }满足:
}满足:![]() ,且对于任意的正整数m,n都有
,且对于任意的正整数m,n都有![]() ,则
,则
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
解析:数列![]() 满足:
满足: ![]() , 且对任意正整数
, 且对任意正整数![]() 都有
都有![]()
![]() ,
,![]() ,∴数列
,∴数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列。
的等比数列。![]()
![]() ,选A.
,选A.
2.(陕西卷) n→∞lim等于( )
A. 1 B. C. D.0
解析:n→∞lim=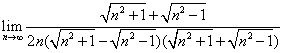
=![]() ,选B.
,选B.
3.(四川卷)已知![]() ,下面结论正确的是
,下面结论正确的是
(A)![]() 在
在![]() 处连续
(B)
处连续
(B)![]()
(C)![]() (D)
(D)![]()
解析:已知![]() ,则
,则![]() ,而
,而![]() ,∴ 正确的结论是
,∴ 正确的结论是![]() ,选D.
,选D.
二、填空题(共13题)
4.(安徽卷)设常数![]() ,
,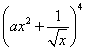 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则![]() __________。
__________。
解:![]() ,由
,由![]()
![]() ,所以
,所以 ,所以为1。
,所以为1。
5.(北京卷)![]() 的值等于__________________.
的值等于__________________.
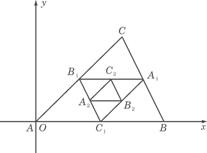 解:
解:![]() =
=![]() =
=![]()
6.(福建卷)如图,连结△ABC的各边中点得到一个新的
△A1B1C1,又连结的△A1B1C1各边中点得到,如此无限继
续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…,
这一系列三角形趋向于一个点M,已知A(0,0) ,B(3,0),C(2,2),
则点M的坐标是 .
解:如图,连结![]() 的各边中点得到一个新的
的各边中点得到一个新的![]() 又连结
又连结![]() 的各边中点得到
的各边中点得到![]() ,如此无限继续下去,得到一系列三角形:
,如此无限继续下去,得到一系列三角形:![]() ,
,![]() ,
,![]() ,
,![]() ,这一系列三角形趋向于一个点M。已知
,这一系列三角形趋向于一个点M。已知![]()
![]() 则点M的坐标是
则点M的坐标是![]() 的重心,∴ M=
的重心,∴ M=![]()
7.(广东卷)、![]()
解析:![]()
8.(湖北卷)将杨辉三角中的每一个数![]() 都换成
都换成![]() ,就得到一个如下图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出
,就得到一个如下图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出![]() ,其中
,其中![]() 。令
。令![]() ,则
,则![]() 。
。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
…
解:第一个空通过观察可得。
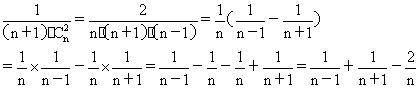
![]() =(1+
=(1+![]() -1)+(
-1)+(![]() )+(
)+(![]() +
+![]() -
-![]() )+(
)+(![]() +
+![]() -
-![]() )+…+(
)+…+(![]() +
+![]() -
-![]() )+(
)+(![]() +
+![]() -
-![]() )
)
=(1+![]() +
+![]() +…+
+…+![]() )+(
)+(![]() +
+![]() +
+![]() +
+![]() +…+
+…+![]() )-2(
)-2(![]() +
+![]() +…+
+…+![]() )
)
=〔(1+![]() +
+![]() +…+
+…+![]() )-(
)-(![]() +
+![]() +…+
+…+![]() )〕+〔(
)〕+〔(![]() +
+![]() +
+![]() +
+![]() +…+
+…+![]() )
)
-(![]() +
+![]() +…+
+…+![]() )〕=1-
)〕=1-![]() +
+![]() -
-![]() =
=![]() +
+![]() -
-![]()
所以![]()
![]()
9.(江西卷)数列{![]() }的前n项和为Sn,则
}的前n项和为Sn,则![]() Sn=______________
Sn=______________
解:![]()
故![]()
![]()
![]()
![]()
![]()
10.(辽宁卷)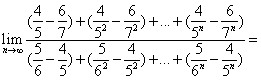 _____________
_____________
【解析】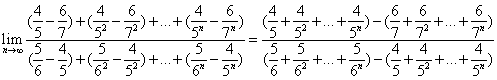
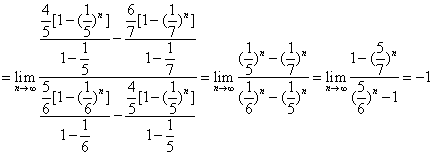
【点评】本题考查了等比数列的求和公式以及数列极限的基本类型.
11.(山东卷)若![]() .
.
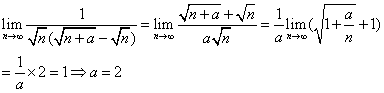 解析:
解析:
12.(上海卷)计算:![]() = .
= .
解: ;
;
13.(上海卷)计算:![]() 。
。
解: ![]()
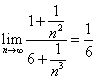 。
。
14.(天津卷)设函数![]() ,点
,点![]() 表示坐标原点,点
表示坐标原点,点![]() ,若向量
,若向量![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,(其中
的夹角,(其中![]() ),设
),设![]() ,则
,则![]() =
.
=
.
解析:函数![]() ,点
,点![]() 表示坐标原点,点
表示坐标原点,点![]() ,若向量
,若向量![]() =
=![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,
的夹角,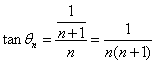 (其中
(其中![]() ),设
),设![]()
![]() ,则
,则![]() =1.
=1.
15.(重庆卷)![]()
![]() _________.
_________.
解:![]()
![]() 。
。
16.(上海春)计算:![]() .
.
解:应用分子分母同除以 n ,便得  从而应填3/4.
从而应填3/4.