普通高等学校招生全国统一考试数学分类汇编
第十章《排列、组合、二项式定理》
一、选择题（共24题）
1．（北京卷）在
这五个数字组成的没有重复数字的三位数中，各位数字之和为奇数的共有
（A）36个 （B）24个 （C）18个 （D）6个
解：依题意，所选的三位数字有两种情况：（1）3个数字都是奇数，有
种方法（2）3个数字中有一个是奇数，有
，故共有＋＝24种方法，故选B
2．（福建卷）从4名男生和3名女生中选出3人，分别从事三项不同的工作，若这3人中至少有1名女生，则选派方案共有
（A）108种 （B）186种 （C）216种 （D）270种
解析：从全部方案中减去只选派男生的方案数，合理的选派方案共有
=186种，选B.
3．（湖北卷）在
的展开式中，
的幂的指数是整数的项共有
A．3项 B．4项 C．5项 D．6项
解：
，当r＝0，3，6，9，12，15，18，21，24时，x的指数分别是24，20，16，12，8，4，0，－4，－8，其中16，8，4，0，－8均为2的整数次幂，故选C
4．（湖南卷）某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有 ( )
A.16种 B.36种 C.42种 D.60种
解析：有两种情况，一是在两个城市分别投资1个项目、2个项目，此时有
种方案，二是在三个城市各投资1个项目，有
种方案，共计有60种方案，选D.
5．（湖南卷）若
的展开式中
的系数是80，则实数a的值是
A．-2 B. 
C. 
D. 2
解析：
的展开式中的系数
=
x3， 则实数
的值是2，选D
6．（湖南卷）在数字1,2，3与符号＋，－五个元素的所有全排列中，任意两个数字都不相邻的全排列个数是
A．6 B. 12 C. 18 D. 24
解析：先排列1，2，3，有
种排法，再将“＋”，“－”两个符号插入，有
种方法，共有12种方法，选B.
7．（江苏卷）
的展开式中含x的正整数指数幂的项数是
（A）0 （B）2 （C）4 （D）6
【思路点拨】本题主要考查二项式展开通项公式的有关知识.
【正确解答】
的展开式通项为
，因此含x的正整数次幂的项共有2项.选B
【解后反思】多项式乘法的进位规则.在求系数过程中,尽量先化简,降底数的运算级别,尽量化成加减运算,在运算过程可以适当注意令值法的运用,例如求常数项,可令
.在二项式的展开式中，要注意项的系数和二项式系数的区别.
8．（江西卷）在（x－
）2006 的二项展开式中，含x的奇次幂的项之和为S，当x＝时，S等于（ ）
A.23008 B.-23008 C.23009 D.-23009
解：设（x－）2006＝a0x2006＋a1x2005＋…＋a2005x＋a2006
则当x＝时，有a0（）2006＋a1（）2005＋…＋a2005（）＋a2006＝0 （1）
当x＝－时，有a0（）2006－a1（）2005＋…－a2005（）＋a2006＝23009 （2）
（1）－（2）有a1（）2005＋…＋a2005（）＝－23009¸2＝－23008，故选B
9．（江西卷）在
的二项展开式中，若常数项为
，则
等于（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
解：
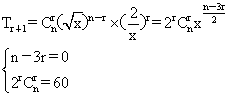，由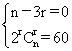
解得n＝6故选B
10．（辽宁卷）
的值为（ ）
Ａ．61 Ｂ．62 Ｃ．63 Ｄ．64
解：原式＝
，选B
11．（全国卷I）设集合
。选择I的两个非空子集A和B，要使B中最小的数大于A中最大的数，则不同的选择方法共有
A．
B．
C．
D．
解析：若集合A、B中分别有一个元素，则选法种数有
=10种；若集合A中有一个元素，集合B中有两个元素，则选法种数有
=10种；若集合A中有一个元素，集合B中有三个元素，则选法种数有
=5种；若集合A中有一个元素，集合B中有四个元素，则选法种数有
=1种；若集合A中有两个元素，集合B中有一个元素，则选法种数有=10种；若集合A中有两个元素，集合B中有两个个元素，则选法种数有=5种；若集合A中有两个元素，集合B中有三个元素，则选法种数有=1种；若集合A中有三个元素，集合B中有一个元素，则选法种数有=5种；若集合A中有三个元素，集合B中有两个元素，则选法种数有=1种；若集合A中有四个元素，集合B中有一个元素，则选法种数有=1种；总计有，选B.
解法二：集合A、B中没有相同的元素，且都不是空集，
从5个元素中选出2个元素，有=10种选法，小的给A集合，大的给B集合；
从5个元素中选出3个元素，有=10种选法，再分成1、2两组，较小元素的一组给A集合，较大元素的一组的给B集合，共有2×10=20种方法；
从5个元素中选出4个元素，有=5种选法，再分成1、3；2、2；3、1两组，较小元素的一组给A集合，较大元素的一组的给B集合，共有3×5=15种方法；
从5个元素中选出5个元素，有=1种选法，再分成1、4；2、3；3、2；4、1两组，较小元素的一组给A集合，较大元素的一组的给B集合，共有4×1=4种方法；
总计为10+20+15+4=49种方法。选B.
12．（全国卷I）在
的展开式中，
的系数为
A．
B．
C．
D．
解析：在
的展开式中，x4项是
=－15x4，选C.
13．（全国II）5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有
（A）150种 (B)180种 (C)200种 (D)280种
解：人数分配上有1,2,2与1,1,3两种方式，若是1,2,2，则有
＝60种，若是1,1,3，则有
＝90种，所以共有150种，选A
14．（山东卷）已知集合A=｛5｝,B=｛1,2｝,C=｛1,3,4｝，从这三个集合中各取一个元素构成空间直角坐标系中点的坐标，则确定的不同点的个数为
(A)33 (B) 34 (C) 35 (D)36
解：不考虑限定条件确定的不同点的个数为
＝36，但集合B、C中有相同元素1，由5，1，1三个数确定的不同点的个数只有三个，故所求的个数为36－3＝33个，选A
15．（山东卷）已知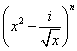
的展开式中第三项与第五项的系数之比为－
,其中
=－1，则展开式中常数项是
(A)－45i (B) 45i (C) －45 (D)45
解：第三项的系数为－
，第五项的系数为
，由第三项与第五项的系数之比为－可得n＝10，则
＝
，令40－5r＝0，解得r＝8，故所求的常数项为
＝45，选A
16．（山东卷）已知(
)
的展开式中第三项与第五项的系数之比为，则展开式中常数项是
(A)－1 (B)1 (C)－45 (D)45
解：第三项的系数为，第五项的系数为，由第三项与第五项的系数之比为可得n＝10，则
＝
，令40－5r＝0，解得r＝8，故所求的常数项为
＝45，选D
17．（天津卷）将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有（ ）
A．10种 B．20种 C．36种 D．52种
解析：将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，分情况讨论：①1号盒子中放1个球，其余3个放入2号盒子，有
种方法；②1号盒子中放2个球，其余2个放入2号盒子，有
种方法；则不同的放球方法有10种，选A．
18．（浙江卷）若多项式
(A)9 (B)10 (C)－9 (D)－10
【考点分析】本题考查二项式展开式的特殊值法，基础题。
解析：令
，得
，
令
，得
19．（浙江卷）函数f:1,2,3
1,2,3满足f(f(x))=
f(x)，则这样的函数个数共有
(A)1个 (B)4个 (C)8个 (D)10个
【考点分析】本题考查抽象函数的定义，中档题。
解析：
即
20（浙江卷）在二项式
的展开式中，含
的项的系数是
(A)15 (B)20 (C)30 (D)40
解析：含的项的系数是
＝20，选B
21．(重庆卷)若
—
n的展开式中各项系数之和为64，则展开式的常数项为
（A）－540 （B）－162 （C）162 （D）540
解析：若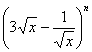
的展开式中各项系数之和为
=64，
，则展开式的常数项为
=－540，选A.
22．(重庆卷)将5名实习教师分配到高一年级的３个班实习，每班至少１名，最多２名，则不同的分配方案有
（A）３０种 （B）９０种 （C）１８０种 （D）２７０种
解析：将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则将5名教师分成三组，一组1人，另两组都是2人，有
种方法，再将3组分到3个班，共有
种不同的分配方案，选B.
23．(重庆卷)
的展开式中
的系数为
（A）－2160 （B）－1080 （C）1080 （D）2160
解：
，由5－r＝2解得r＝3，故所求系数为
＝－1080故选B
24．(重庆卷)高三（一）班学要安排毕业晚会的4各音乐节目，2个舞蹈节目和1个曲艺节目的演出顺序，要求两个舞蹈节目不连排，则不同排法的种数是
（A）1800 （B）3600 （C）4320 （D）5040
解：不同排法的种数为
＝3600，故选B
二、填空题（共21题）
25．（安徽卷）设常数
，
展开式中的系数为
，则＝_____。
解：
，由
。
26．（北京卷）在
的展开式中，的系数中__________________（用数字作答）. 解：
令
得r＝1故 的系数为
＝－14
27。（北京卷）在
的展开式中，x3的系数是
.（用数字作答）
解：
，令7－2r＝3，解得r＝2，故所求的系数为
＝84
28．（福建卷）(x
－
)展开式中x的系数是
(用数字作答)
解：
展开式中，项为
，该项的系数是10.
29．（广东卷）在
的展开式中，
的系数为________.
解：
所以
的系数为
30．（湖北卷）某工程队有6项工程需要单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在工程乙完成后才能进行，有工程丁必须在工程丙完成后立即进行。那么安排这6项工程的不同排法种数是 。（用数字作答）
解：依题意，只需将剩余两个工程插在由甲、乙、丙、丁四个工程形成的5个空中，可得有
＝20种不同排法。
31．（湖北卷）安排5名歌手的演出顺序时，要求某名歌手不第一个出场，另一名歌手不最后一个出场，不同排法的总数是 .(用数字作答)
解：分两种情况：（1）不最后一个出场的歌手第一个出场，有
种排法（2）不最后一个出场的歌手不第一个出场，有
种排法，故共有78种不同排法
32．（湖南卷）若
的展开式中的系数是-80,则实数的值是
.
解：的展开式中的系数
=
x3， 则实数的值是－2.
33．（江苏卷）今有2个红球、3个黄球、4个白球，同色球不加以区分，将这9个球排成一列有 种不同的方法（用数字作答）。
【思路点拨】本题考查排列组合的基本知识.
【正确解答】由题意可知，因同色球不加以区分，实际上是一个组合问题，共有
【解后反思】分步计数原理与分类计数原理是排列组合中解决问题的重要手段,也是基础方法,在高中数学中,只有这两个原理,尤其是分类计数原理与分类讨论有很多相通之处,当遇到比较复杂的问题时,用分类的方法可以有效的将之化简,达到求解的目的.
34．（辽宁卷）5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.(以数作答)
【解析】两老一新时, 有
种排法;
两新一老时, 有
种排法,即共有48种排法.
【点评】本题考查了有限制条件的排列组合问题以及分类讨论思想.
35．（全国卷I）安排7位工作人员在5月1日到5月7日值班，每人值班一天，其中甲、乙二人都不能安排在5月1日和2日，不同的安排方法共有__________种。（用数字作答）解析：先安排甲、乙两人在后5天值班，有
=20种排法，其余5人再进行排列，有
=120种排法，所以共有20×120=2400种安排方法。
36（全国II）在(x4＋)10的展开式中常数项是 （用数字作答）
解析：
要求常数项,即40-5r=0,可得r=8代入通项公式可得
37．(陕西卷) (3x－)12展开式x－3的系数为 (用数字作答)
解析：(3x－)12展开式中，x－3项为
=594
，的系数是594．
38．(陕西卷)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有 种
解析：某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人)，其中甲和乙不同去，甲和丙只能同去或同不去，可以分情况讨论，① 甲、丙同去，则乙不去，有
=240种选法；②甲、丙同不去，乙去，有
=240种选法；③甲、乙、丙都不去，有
种选法，共有600种不同的选派方案．
39．(陕西卷) (2x－)6展开式中常数项为 (用数字作答)
解析：(2x－)6展开式中常数项
.
40．(陕西卷)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人)，其中甲和乙不同去，则不同的选派方案共有 种 ．
解析：可以分情况讨论，① 甲去，则乙不去，有
=480种选法；②甲不去，乙去，有=480种选法；③甲、乙都不去，有
=360种选法；共有1320种不同的选派方案．
41．（四川卷）
展开式中的系数为 （用数字作答）
解析：展开式中的项为
，的系数为－960。
42．（天津卷）
的二项展开式中的系数是____ （用数学作答）．
解析：的二项展开式中的项是
，所以x的系数是280．
43．（天津卷）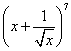
的二项展开式中的系数是 （用数字作答）．
解析：
的二项式展开式中项为
，x项的系数是35.
44．（天津卷）用数字0，1，2，3，4组成没有重复数字的五位数，则其中数字1，2相邻的偶数有 个（用数字作答）．
解析：可以分情况讨论：① 若末位数字为0，则1，2，为一组，且可以交换位置，3，4，各为1个数字，共可以组成
个五位数；② 若末位数字为2，则1与它相邻，其余3个数字排列，且0不是首位数字，则有
个五位数；③ 若末位数字为4，则1，2，为一组，且可以交换位置，3，0，各为1个数字，且0不是首位数字，则有
=8个五位数，所以全部合理的五位数共有24个。
45．（上海春）电视台连续播放6个广告，其中含4个不同的商业广告和2个不同的公益广告，要求首尾必须播放公益广告，则共有 种不同的播放方式（结果用数值表示）.
解：分二步：首尾必须播放公益广告的有A22种；中间4个为不同的商业广告有A44种，从而应当填 A22·A44＝48. 从而应填48．