第一学期第二次教学质量检测高三级理科数学试卷
考试时间：120分钟
一、选择题：本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有
一项是符合题目要求的.
1. 设集合
≤x≤2},B={x0≤x≤4},则A∩B=
A．［0,2］ B．［1,2］ C．［0,4］ D．［1,4］
2. 已知函数
，若
则
A．
B．－
C．2
D．－2
3．有关命题的说法错误的是
A．命题“若
则
”的逆否命题为：“若
，
则
”。
B．“”是“”的充分不必要条件。
C．若
为假命题，则
、
均为假命题。
D．对于命题
：
使得
. 则
：
均有
。
4. 一条直线若同时平行于两个相交平面，则这条直线与这两个平面交线的位置关系是
A．相交 B．平行 C．异面 D．不确定
5. 函数
的图象的大致形状是
6.等比数列
前n项的积为Tn，若
是一个确定的常数，则下列各数也是常数的是
A．
B．
C．
D．
7.已知函数
若
则
A．
B．
C．
D．
与
的大小不能确定
8. 有一个棱长均为
的正四棱锥（底面是正方形，顶点在底面的射影是底面的中心），现用一张正方形的包装纸将其完全包住，不能裁剪，可以折叠，那么包装纸的最小边长为
A．(1+
)a B．
a C．
a D．(
+
)a
二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卷中相应的横线上.
9．若
，则
_____
10.三条直线
与
相交于一点，则的值为______
11. 如图是一个空间几何体的三视图，若等边三角
形的边长为2，那么该几何体的体积为__________
12. 函数
的单调递增区间是
13．设
为正数，则
的最小值是_____________
14．设约束条件为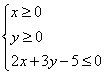
，则目标函数
的最大值为_________。
三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤。
15．（本小题满分14分）已知函数
（Ⅰ）若
，求函数
在
的值域；
（Ⅱ）若
，求不等式
的解集；
（Ⅲ）若函数
在
上是单调减函数，求实数的取值范围。
16．（本小题满分14分）已知函数
（Ⅰ）求的最小正周期；
（Ⅱ）在△ABC中，、
、
分别是A、B、C的对应边，若
，求的长。
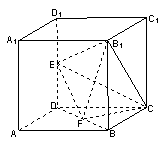17．（本小题满分14分）如图所示，在正方体
中，
、
分别为
、
的中点．
（Ⅰ）求证：
//平面
；
（Ⅱ）求证：
；
（Ⅲ）求二面角
的平面角的余弦值。
18．（本小题满分12分）某工厂统计资料显示，产品次品率P与日产量
件的关系为
。又知每生产一件正品盈利元，每生产一件次品损失
元（
）
（Ⅰ）将该厂日盈利额T元表示为日产量件的函数；
（Ⅱ）为了获得最大盈利，该厂的日产量应定为多少件？（取在
1. 732计算）
19．（本题满分12分）已知平面上定点
的坐标是
，动点
满足
。
（Ⅰ）求动点D的轨迹方程；
（Ⅱ）在轨迹D上任取一点P，求
的最小值及取得最小值时点P的坐标。
20．（本小题满分14分）把正奇数数按上小下大、左小右大的原则排成如下三角形数表（第n行有n个数，如下表）：
1
3 5
7 9 11
— — — —
— — — — —
（I）第六行的第一个数是什么？
（II）若记三角形数表中第n行各数的和为
，
①猜想的表达式，并证明；
②记
，求证：
；
（Ⅲ）设
是位于这个三角形数表中第
行中第
个数，若
，求
的值。
饶平二中2006学年度第一学期第二次教学质量检测
高三级理科数学答题卷
高_____年级______班、座号_______姓名___________得分____________
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
一．选择题
二．填空题9._______ 10._________ 11.________ 12. 13.________14.
三．解答题
| 15．（本小题满分14分） |
| 16． （本小题满分14分）
|
|
|
| 18．（本小题满分12分） |
高_____年级______班、座号_______姓名___________
| 19．（本小题满分12分） |
| 20．（本小题满分14分） |