第一学期高三年级数学学科期中考试卷
一、填空题：（每题4分，共48分）
1．函数
的定义域是__________。
2．设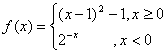
，若
>8,则
的取值范围为______________。
3．计算：
＝__________。
4．已知Z是复数，且满足2Z+Z
=0，则Z=________________。
5．已知函数
在区间
是减函数，则实数
的取值范围_____________。
6．
是首项
,公差
=3的等差数列,如果
,则序号
等于____。
7．在
ABC中，∠C=1200，c=7，
，则S
=____________。
8．在数学拓展课上，老师规定了一种运算:
,例如：1*2=1，3*2=2，则函数
的值域为 。
9．若不等式
对于任意正整数恒成立，则实数的取值范围是___________。
10．十六大报告提出，我国要在本世纪头二十年，集中力量全面建设成小康社会，国内生产总值到2020年力争比2000年翻两番，按照这一目标，到2020年，我国国内生产总值将达到35万亿元，假设这20年我国经济年增长速度相同，那么到________年我国国内生产总值将达到20万亿元。
11．方程lgx=sinx的最大根为__________。（精确到0.1）
12．已知函数
的值域为[－2，3），则函数
的一个可能解析式是_________________________。x
[0,+
)
二、选择题：（每题4分，共16分）
13．已知Z为复数，若
，则复数
是
（ ）
（A）实数 （B）虚数但不一定是纯虚数
（C）纯虚数 （D）可能是虚数也可能是纯虚数
14．若奇函数在（0，+）是增函数，又
=0，则{x
＜0}的解集为 （ ）
（A）（-3,0）∪（3, +） （B）（-3,0）∪（0,3）
（C）（-,-3）∪（3,+） （D）（-,-3)∪（0,3）
15．若函数
与函数
在
上的单调性相同，则
中的一个值为
（
）
（A）
（B）
（C）
（D）
16．设是公比为（
）、首项为
的等比数列，
是前项的和，对任意N，点（，
）
（
）
（A）在直线
上
（B）在直线
上
（C）在直线
上
（D）在直线
上
三、解答题：
17．（本题12分）设集合A={
－
2}，B={
}，若A
B，求实数的取值范围。
18．（本题12分）已知函数
。
（1）当
时，求函数的最小值：
（2）若对任意
恒成立，试求实数的取值范围。
19．（本题14分）已知数列满足，
(n≥2)
（1）求
，
； （2）求的通项公式。
20．（本题14分）已知函数
的图像与函数
的图像关于点A
对称。
（1）求的值。
（2）若
在区间
上为减函数，求实数的取值范围。
21．（本题16分）某企业去年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降。若不能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为500(1+
)万元（n为正整数）。
（1）设从今年起的n年内，若该企业不进行技术改造的累计纯利润为
万元，进行技术改造后的累计纯利润为
万元（须扣除技术改造资金），求、的表达式；
（2）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？
22．（本题18分）函数=
(、是非零实常数)，满足
=1，且方程=x有且仅有一个解。
(1)求、的值；
(2)是否存在实常数m，使得对定义域中任意的x，+
=4恒成立？为什么？
(3)在直角坐标系中，求定点A(–3,1)到此函数图像上任意一点P的距离AP的最小值。