第一学期高三年级数学学科学习能力诊断卷
(考试时间120分,满分120分)
(第一部分、文理合卷)
一、填空题:(本小题满分40分,每小题4分)
1.
函数![]() 的递减区间是_____________
的递减区间是_____________
2.若集合![]() ,则
,则![]() =______________
=______________
3.函数![]() 的最小正周期是_____________
的最小正周期是_____________
4.复数![]() =______________ (
=______________ (![]() 是虚数单位)
是虚数单位)
5.设![]() 是数列
是数列![]() 的前n项和,若
的前n项和,若![]() ,则
,则![]() =______________
=______________
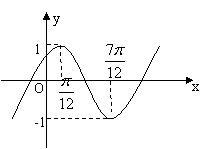 6.函数
6.函数![]() 的图象如图所示,
的图象如图所示,
则函数的解析式是_____________
7.若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的
的
右焦点重合,则![]() 的值是____________
的值是____________
8.![]() =________________ 。(
=________________ 。(![]() 是自然数)
是自然数)
9.已知![]() 的三个内角
的三个内角![]() 成等差数列,且
成等差数列,且![]() ,则边
,则边![]() 上的中线
上的中线![]() 的长为_____________
的长为_____________
10.函数 的反函数是_________________
的反函数是_________________
二、选择题:(本题满分12分,每小题4分)
11.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用抽样法,抽取一个样本容量为90人的样本,应在这三校分别抽取学生…………………………………………………………………………………( )
(A) 30人,30人,30人 (B) 30人,45人,15人
(C) 20人,30人,10人 (D) 30人,50人,10人
12.设![]() 是上的任意函数,则下列叙述正确的是…………………………………( )
是上的任意函数,则下列叙述正确的是…………………………………( )
(A) ![]() 是奇函数 (B)
是奇函数 (B) ![]() 是奇函数
是奇函数
(C) ![]() 是偶函数
(D)
是偶函数
(D) ![]() 是偶函数
是偶函数
13.从圆![]() 外一点向
外一点向![]() 这个圆作两条切线,则两条切线夹角的余弦值是……………………………………………………………………………………( )
这个圆作两条切线,则两条切线夹角的余弦值是……………………………………………………………………………………( )
(A) ![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)
![]()
三、解答题:
14.(本题满分12分)
解不等式组:
15.(本题满分12分)
已知![]() ,
,![]()
(1)
求![]() 的值;(6分)
的值;(6分)
(2) 求![]() 的值。(6分)
的值。(6分)
16。(本题满分14分)
在等差数列![]() 中,前
中,前![]() 项和
项和![]() 满足
满足![]()
(1) 求数列![]() 的通项公式;(7分)
的通项公式;(7分)
(2) 记![]() ,求
,求![]() 。(7分)
。(7分)
17。(本题满分14分)
统计表明,某种型号的大型卡车在匀速行驶中每小时的耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:![]() ,已知甲、乙两地相距100千米。
,已知甲、乙两地相距100千米。
(1) 当卡车以40千米/小时的速度匀速行驶时,从甲地到乙地在耗油多少升?(7分)
(2) 当卡车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?(7分)
(第二部分、文理分叉)
四、理科做,文科不做(其中18~20题各4分)
18。设![]() 是某三角形的最大内角,且满足
是某三角形的最大内角,且满足![]() ,则满足上述条件的
,则满足上述条件的![]() 的可能值有( )
的可能值有( )
(A) 2个 (B) 3个 (C) 4个 (D) 5个
19。已知椭圆![]() 的长轴端点为
的长轴端点为![]() ,将线段
,将线段![]() 分成10份,过每个分点作x轴的垂线交椭圆的上半部分于
分成10份,过每个分点作x轴的垂线交椭圆的上半部分于![]() 九个点,F是椭圆的一个端点,则
九个点,F是椭圆的一个端点,则![]() =___________________
=___________________
20。对于函数![]() ,在使
,在使![]() 成立的所有常数
成立的所有常数![]() 中,我们把
中,我们把![]() 的最大值
的最大值![]() 叫做函数
叫做函数![]() 的下确界。设有函数
的下确界。设有函数![]() 试问:该函数是否有下确界,若有,求出
试问:该函数是否有下确界,若有,求出![]() 的值,若没有,就填写没有____________。
的值,若没有,就填写没有____________。
21。(本题满分16分)
已知两定点![]() ,曲线
,曲线![]() 上的动点
上的动点![]() 满足条件
满足条件![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 相切。
相切。
(1)求曲线![]() 的方程;(5分)
的方程;(5分)
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值;(5分)
的值;(5分)
(3)设![]() 为坐标原点,过(2)中的点
为坐标原点,过(2)中的点![]() 及点
及点![]() 作平行四边形
作平行四边形![]() ,设
,设![]() 为线段
为线段![]() 与曲线
与曲线![]() 的交点,求
的交点,求![]() 的面积
的面积![]() 。
。
22。(本题满分18分)
已知函数![]()
(1) 求函数![]() 的定义域和值域;(5分)
的定义域和值域;(5分)
(2) 设![]() (
(![]() 为实数),求
为实数),求![]() 的最大值
的最大值![]() ;(8分)
;(8分)
(3) 若![]() 对所有的实数
对所有的实数![]() 及
及![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。(5分)
的取值范围。(5分)
五、文科做,理科不做(其中18~20题各4分)
18。![]() 的值( )
的值( )
(A) 小于0 (B) 大于0 (C) 等于0 (D)不存在
19。设直线![]() 的倾斜角为
的倾斜角为![]() ,则它关于直线
,则它关于直线![]() 对称的直线的倾斜角是__________(用
对称的直线的倾斜角是__________(用![]() 表示)
表示)
20。函数![]() 的最大值为________________
的最大值为________________
21。(本题满分16分)
已知与曲线![]() 相切的直线
相切的直线![]() 交于
交于![]() 轴于
轴于![]() 两点,
两点,![]() 为原点,
为原点,![]()
(1) 求证:![]() (6分)
(6分)
(2) 求线段AB中点的轨迹方程;(5分)
(3) 求![]() 面积的最小值。(5分)
面积的最小值。(5分)
22。(本题满分18分)
已知二次函数![]() 的对称轴为
的对称轴为![]() ,且方程
,且方程![]() 有两个相等的实数根。
有两个相等的实数根。
(1) 求![]() 的解析式;(8分)
的解析式;(8分)
(2) 求![]() 在[1, 3]上的值域;(4分)
在[1, 3]上的值域;(4分)
(3) 是否存在实数![]() ,使
,使![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值 (只要求出一个
的值 (只要求出一个![]() 值即可) ,若不存在,请说明理由。(6分)
值即可) ,若不存在,请说明理由。(6分)