高考数学高等学校招生全国统一考试38
本试卷分第Ⅰ部分(选择题)和第Ⅱ部分(非选择题)共150分 考试时间120分钟.
第Ⅰ部分(选择题 共60分)
参考公式:
如果事件A、B互斥,那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]()
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)函数![]() 的定义域是 (A)
的定义域是 (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2)函数![]() , 则
, 则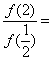
(A)1
(B)-1
(C)![]() (D)
(D)![]()
(3)圆![]() 的圆心到直线
的圆心到直线![]() 的距离为 (A)2 (B)
的距离为 (A)2 (B)![]() (C)1
(D)
(C)1
(D)![]()
(4)不等式![]() 的解集是
的解集是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(5)![]() (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则向量
,则向量![]() 的模为 (A)2 (B)4
(C)6 (D)12
的模为 (A)2 (B)4
(C)6 (D)12
(7)已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件。那么p是q成立的:
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(8)不同直线![]() 和不同平面
和不同平面![]() ,给出下列命题
,给出下列命题
① ![]() ②
② ![]()
③ ![]() ④
④ ![]()
其中假命题有:
(A)0个 (B)1个 (C)2个 (D)3个
(9) 若![]() 是等差数列,首项
是等差数列,首项![]() ,则使前n项和
,则使前n项和![]() 成立的最大自然数n是
成立的最大自然数n是
(A)4005 (B)4006 (C)4007 (D)4008
(10)已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且![]() ,则此双曲线的离心率e的最大值为
,则此双曲线的离心率e的最大值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)已知盒中装有3只螺口与7只卡口灯炮,这些灯炮的外形与功率都相同且灯口向下放着,现需要一只卡口灯炮使用,电工师傅每次从中任取一只并不放回,则他直到第3次才取得卡口灯炮的概率为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(12)如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是
(A)258 (B)234 (C)222 (D)210

第Ⅱ部分(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)若在![]() 的展开式中
的展开式中![]() 的系数为
的系数为![]() ,则
,则![]()
(14)已知![]() ,则
,则![]() 的最小值是____________
的最小值是____________
(15)已知曲线![]() ,则过点
,则过点![]() 的切线方程是______________
的切线方程是______________
(16)毛泽东在《送瘟神》中写到:“坐地日行八万里”。又知地球的体积大约是火星的8倍,则火星的大圆周长约为______________万里.
三、解答题:本题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
求函数![]() 的最小正周期和最小值;并写出该函数在
的最小正周期和最小值;并写出该函数在![]() 上的单调递增区间.
上的单调递增区间.
(18)(本小题满分12分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5。
(1)三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率;
(2)若甲单独向目标射击三次,求他恰好命中两次的概率.
(19)(本小题满分12分)
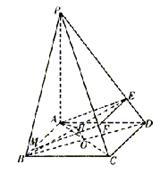
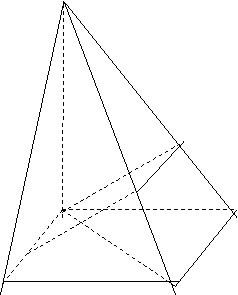
如图,四棱锥P-ABCD的底面是正方形, ![]()
(1) 证明MF是异面直线AB与PC的公垂线;
(2)若![]() ,求二面角E—AB—D平面角.
,求二面角E—AB—D平面角.
 |
|
|
|
|
|
|
|
|
(20)(本小题满分12分)
某工厂生产某种产品,已知该产品的月生产量![]() (吨)与每吨产品的价格
(吨)与每吨产品的价格![]() (元/吨)之间的关系式为:
(元/吨)之间的关系式为:![]() ,且生产x吨的成本为
,且生产x吨的成本为![]() (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
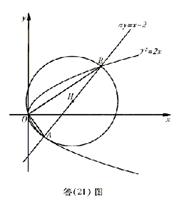
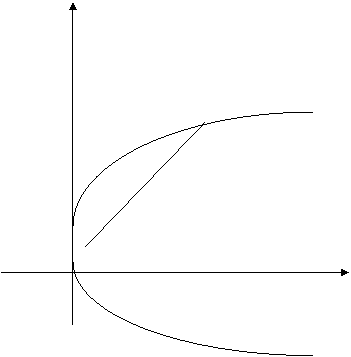
(21)(本小题满分12分)
设直线![]() 与抛物线
与抛物线![]() 交于相异两点A、B,以线段AB为直经作圆H(H为圆心). 试证抛物线顶点在圆H的圆周上;并求a的值,使圆H的面积最小.
交于相异两点A、B,以线段AB为直经作圆H(H为圆心). 试证抛物线顶点在圆H的圆周上;并求a的值,使圆H的面积最小.
|
 |
|
|

|
|
|
|
|
(22)(本小题满分14分)
设![]()
(1)令![]() 求数列
求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前n项和
的前n项和![]() .
.
数学(文史类)参考答案
一、选择题:每小题5分,共60分.
(1)D (2)B (3)D (4)A (5)B (6)C
(7)A (8)D (9)B (10)B (11)D (12)C
二、填空题:每小题4分,共16分.
(13)-2 (14)6
(15)![]() (16)4
(16)4
三、解答题:共74分.
(17)(本小题12分)
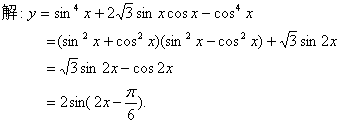
故该函数的最小正周期是![]() ;最小值是-2;
;最小值是-2;
单增区间是![]()
(18)(本小题12分)
解:(I)设AK表示“第k人命中目标”,k=1,2,3.
这里,A1,A2,A3独立,且P(A1)=0.7,P(A2)=0.6,P(A3)=0.5.
从而,至少有一人命中目标的概率为
![]()
恰有两人命中目标的概率为
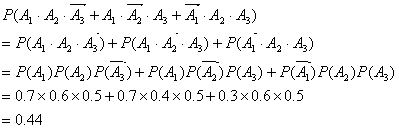
答:至少有一人命中目标的概率为0.94,恰有两人命中目标的概率为0.44
(II)设甲每次射击为一次试验,从而该问题构成三次重复独立试验.又已知在每次试验中事件“命中目标”发生的概率为0.7,故所求概率为
![]()
答:他恰好命中两次的概率为0.441.
|
(I)证明:因PA⊥底面,有PA⊥AB,又知AB⊥AD,
故AB⊥面PAD,推得BA⊥AE,
又AM∥CD∥EF,且AM=EF,
证得AEFM是矩形,故AM⊥MF.
又因AE⊥PD,AE⊥CD,故AE⊥面PCD,
而MF∥AE,得MF⊥面PCD,
故MF⊥PC,
因此MF是AB与PC的公垂线.
(II)解:因由(I)知AE⊥AB,又AD⊥AB,
故∠EAD是二面角E—AB—D的平面角.
设AB=a,则PA=3a.
因Rt△ADE~Rt△PDA
故∠EAD=∠APD
因此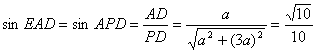 .
.
(20)(本小题12分)
解:每月生产x吨时的利润为![]()
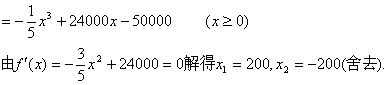
![]() ,故它就是最大值点,且最大值为:
,故它就是最大值点,且最大值为:![]()
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
(21)(本小题12分)
解法一:设![]() ,则其坐标满足
,则其坐标满足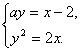
|
则 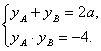
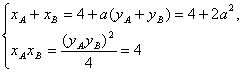
因此![]() .
.
故O必在圆H的圆周上.
又由题意圆心H(![]() )是AB的中点,故
)是AB的中点,故
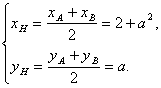
由前已证,OH应是圆H的半径,且![]() .
.
从而当a=0时,圆H的半径最小,亦使圆H的面积最小.
解法二:
设![]() ,则其坐标满足
,则其坐标满足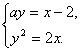
分别消去x,y得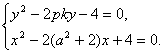
故得A、B所在圆的方程![]()
明显地,O(0,0)满足上面方程
故A、B、O三点均在上面方程的表示的圆上.
又知A、B中点H的坐标为![]()
故 ![]()
而前面圆的方程可表示为![]()
故OH为上面圆的半径R,从而以AB为直径的圆必过点O(0,0).
又![]() ,
,
故当a=0时,R2最小,从而圆的面积最小,
解法三:同解法一得O必在圆H的圆周上
又直径AB=![]()
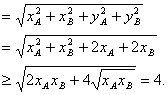
上式当![]() 时,等号成立,直径AB最小,从而圆面积最小.
时,等号成立,直径AB最小,从而圆面积最小.
此时a=0.
(22)(本小题14分)
解:(I)因![]()
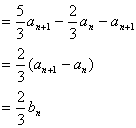
故{bn}是公比为![]() 的等比数列,且
的等比数列,且![]()
![]()
(II)由![]()
![]()
![]()
注意到![]() 可得
可得
![]()
记数列![]() 的前n项和为Tn,则
的前n项和为Tn,则