高考数学普通高等学校全国统一考试76

高考数学普通高等学校全国统一考试76

理科数学（必修＋选修Ⅱ）

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页，第Ⅱ卷3至9页。考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷

注意事项：

1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。不能答在试题卷上。

3. 本卷共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　 　  球是表面积公式

　　　　　　　　　　　　 

如果事件A、Ｂ相互独立，那么　　　　　　　　　　  　　 其中R表示球的半径

　　　　　　　　　　　  球的体积公式

如果事件A在一次试验中发生的概率是P，那么　　　　　 

n次独立重复试验中恰好发生k次的概率　　　　　　  其中R表示球的半径

　

一、选择题

（１）函数的最小正周期是

（A）　　　（B）　　  （C）　　 （D）

解：∵f(x)=sinx+cosx=sin(x+),∴T=,的最小正周期是π.选(C)

（２）正方体中，、、分别是、、的中点．那么，正方体的过、、的截面图形是

（A）　　　三角形（B）四边形（C）五边形（D）六边形

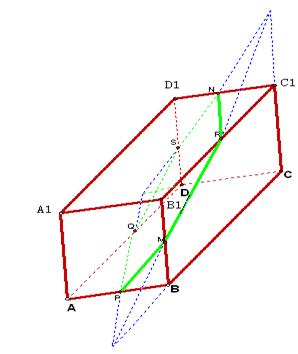
解：如图, 正方体的过、、的截面图形是六边形PMRSQ,选(D)

（３）函数的反函数是

（A）（B）

（C）（D）

解：由函数,得x= -(y≥-1),∴函数的反函数是,选(B)

（４）已知函数在内是减函数，则

（A）　　　０＜≤１（B）－１≤＜０（C）≥１（D）≤－１

解：可用排除法,∵当ω>0时正切函数在其定义域内各长度为一个周期的连续区间内为增函数,∴排除(A)，(C),又当ω>1时正切函数的最小正周期长度小于π,∴在内不连续,在这个区间内不是减函数,这样排除(D),故选(B)。

（５）设、、、，若为实数，则

（A）（B）

（C）（D）

解：∵=,∴当且仅当bc-ad=0时为实数,选(C)

（６）已知双曲线的焦点为、，点在双曲线上且轴，则到直线的距离为

（A）（B）（C）（D）

解：由得a=2,c=3,M(-3,),F₁(-3,0),F₂(3,0),MF₁=

∴F₂M=,由F₁F₂×MF₁=MF₂×h,得h=,选(C)

（７）锐角三角形的内角、满足，则有

（A）（B）

（C）（D）

解：由得,2sin(A-B)sinA=cosB,,cos(2A-B)=0

∵A,B为锐角∴,∴,∴sin2A-cosB=0,选((A)

（８）已知点，，．设的平分线与相交于，那么有，其中等于

（A）　　  ２（B）（C）－３（D）－

解：由已知得,且1+λ<0,即,又∵∴-1-λ=2,∴λ=-3,选(C)

（９）已知集合，，则为

（A）或（B）或

（C）或　　　　（D）或

解：∵M=[-4,7],N=(-∞,-2)∪(3,+∞),∴M∩N={x-4≤x<-2或3<x≤+7},选(A)

（10）点在平面上作匀速直线运动，速度向量（即点的运动方向与相同，且每秒移动的距离为个单位）．设开始时点的坐标为（－１０，１０），则５秒后点的坐标为

（A）（-2，4）（B）（-30，25）（C）（10，-5）（D）（5，-10）

解：设5秒后点P运动到点A,则,

∴=(10,-5),选(C)

（11）如果，，…，为各项都大于零的等差数列，公差，则

（A）（B）（C）++（D）=

解：本题是单项选择题，可用举实例的方法来决定选择支，最简单的例子如1，2，3，4，5，6，7，8。显然只有1×8<4×5,即a₁×a₈<a₄×a₅,,故选(B)

（12）将半径都为１的４个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为

（A）（B）2+（C）4+（D）

解：显然4个钢球两两相切且每个钢球与四面体也相切时，这个正四面体的高最小。这时4个钢球的球心构成一个小正四面体，其底面中心到大正四面体距离是小钢球的半径1，设小正四面体顶点距大正四面体顶点为x，大正四面体的棱长为a，高为h，小正四面体的高为m,则h=,m=,大正四面体底面中心到底面边的距离n=,侧面斜高y=,由平几知识可得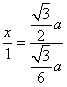=3,得x=3,故h=3+1+m=4+,选(C)

第Ⅱ卷

注意事项：

1．用钢笔或圆珠笔直接答在试题卷上

2．答卷前将密封线内的项目填写清楚

3．本卷共10小题，共90分

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上

（13）圆心为(1,2)且与直线相切的圆的方程为_____________．

解：圆心(1,2)到直线5x-12y-7=0的距离r=,故所求的圆的方程为(x-1)²+(y-2)²=4

（14）设为第四象限的角，若，则_____________．

解：sin3α=3sinα-4sin³α,由已知行3-4sin²α=,得sinα=-,cosα=,tanα＝,∴tan2α=.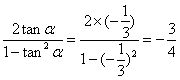

（15）在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被５整除的数共有_____________个．

解：不能被5整除的有两种情况：情况1、首位为5有种，情况2、首位不是5的有种，故在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被５整除的数共有+=192(个)．

（16）下面是关于三棱锥的四个命题：

①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．

②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．

③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥．

④侧棱与底面所成的角相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．

其中，真命题的编号是_____________．（写出所有真命题的编号）

解：正确的命题为①④

三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤

（17）（本小题满分12分）

设函数，求使的取值范围．

（18） （本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…．

（Ⅰ）证明为等比数列；

（Ⅱ）如果无穷等比数列各项的和，求数列的首项和公差．

（注：无穷数列各项的和即当时数列前项和的极限）

（19）（本小题满分12分）

甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.6，本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响．令为本场比赛的局数．求的概率分布和数学期望．（精确到0.0001）

（20）（本小题满分12分）

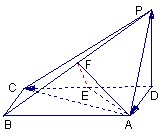
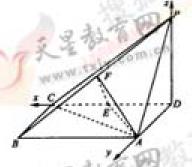
如图，四棱锥P-ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD，E、F分别为CD、PB的中点．

（Ⅰ）求证：EF垂直于平面PAB；

（Ⅱ）设AB=BC，求AC与平面AEF所成的角的大小．

（21）（本小题满分14分）

P、Q、M、N四点都在椭圆上，F为椭圆在y轴正半轴上的焦点．已知与共线，与共线，且．求四边形PMQN的面积的最小值和最大值．

（22）（本小题满分12分）

已知，函数．

（Ⅰ）当x为何值时，f(x)取得最小值？证明你的结论；

（Ⅱ）设f(x)在[-1,1]上是单调函数，求a的取值范围．

2005年普通高等学校招生全国统一考试理科数学（必修＋选修Ⅱ）

参考答案

一、选择题

CDABC  CADAC　BD

二、填空

13 （x－1）²＋（y－2）²＝4；　　　14、－ ； 15、 384；16、①②③④

三、解答题：

17、本小题主要考查指数函数的性质、不等式性质和解法，考查分析问题的能力和运算能力

解：∵f （x）＝2^{x＋1－x－1}≥2＝， 即x＋1－x－1≥．

当x≤ －1时，原不等式化为：－2≥（舍）；

当－1<x≤ 1时，原不等式化为：2x≥ ∴x≥．

∴此时，≤ x≤ 1；

当x>1时， 原不等式化为：2≥，

此时，x>1．

故原不等式的解集为：{xx≥ }．

18、本小题主要考查等差数列、等比数列的基本知识以及运用这些知识的能力

（Ⅰ）证明：设{a_n}中首项为a₁，公差为d．

∵lga₁，lga₂，lga₄成等差数列　∴2lga₂＝lga₁·lga₄ ∴a₂²＝a₁·a₄．

即（a₁＋d）²＝a₁（a₁＋3d）　 ∴d＝0或d＝a₁．

当d＝0时， a_n＝a₁， b_n＝， ∴，∴为等比数列；

当d＝a₁时， a_n＝na₁ ，b_n＝，∴，∴为等比数列．

综上可知为等比数列．

（Ⅱ）∵无穷等比数列{b_n }各项的和

∴q<1， 由⑴知，q＝， d＝a₁ ． b_n＝

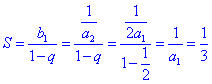∴， ∴a₁＝3．

∴．

19、本小题考查离散型随机变量分布列和数学期望等概念，考查运用概率知识解决实际问题的能力

解：ξ的所有取值为3，4，5

P（ξ＝3）＝；

P（ξ＝4）＝；

P（ξ＝5）＝．

ξ	3	4	5
P	0．28	0．3744	0．3466

∴ξ的分布列为：

∴Eξ＝3×0．28＋4×0．3744＋5×0．3456＝0．84＋1．4976＋1．728＝4．0656．

20、本小题主要考查直线与平面垂直、直线与平面所成角的有关知识、及思维能力和空间想象能力，考查应用向量知识解决数学问题的能力

解：方法一：

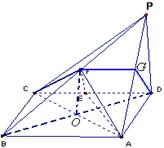（Ⅰ）取PA中点G， 连结FG， DG．

 

．

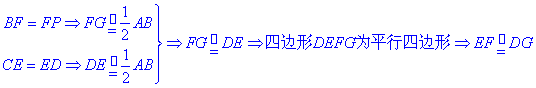
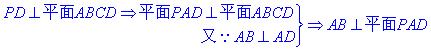
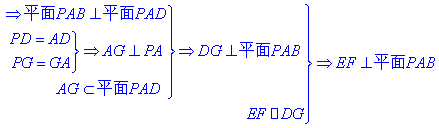（Ⅱ）设AC， BD交于O，连结FO．

．

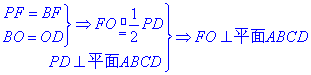设BC＝a， 则AB＝a， ∴PA＝a， DG＝a＝EF， ∴PB＝2a， AF＝a．

设C到平面AEF的距离为h．

∵V_C－AEF＝V_F－ACE， ∴． 即　∴． ∴AC与平面AEF所成角的正弦值为．

即AC与平面AEF所成角为．

21、本小题主要考查椭圆和直线的方程与性质，两条直线垂直的条件、两点间的距离、不等式的性质等基本知识及综合分析能力

解：∵． 即．

当MN或PQ中有一条直线垂直于x轴时，另一条直线必垂直于y轴． 不妨设MN⊥y轴，则PQ⊥x轴．

∵F（0， 1） ∴MN的方程为：y＝1，PQ的方程为：x＝0分别代入椭圆中得：MN＝， PQ＝2．

∴S_{四边形PMQN}＝MN·PQ＝××2＝2．

当MN，PQ都不与坐标轴垂直时，设MN的方程为y＝kx＋1 （k≠0），代入椭圆中得：（k²＋2）x²＋2kx－1＝0，　∴x₁＋x₂＝， x₁·x₂＝．

∴

同理可得：．

∴S_四边形MQN＝MN·PQ＝

＝，

（当且仅当即时，取等号）．

又S_{四边形PMQN} ＝，∴此时， S_{四边形PMQN}．

综上可知：（S_{四边形PMQN} ）_max＝2，  （S_{四边形PMQN} ）_min＝．

22、本小题主要考查导数的概念和计算，应用导数研究函数性质的方法及推理和运算能力

解：（Ⅰ）令＝0　即[x²－2（a－1）x－2a]e^x＝0　∴x²－2（a－1）x－2a＝0

∵△＝[2（a－1）]²＋8a＝4（a²＋1）>0　∴x₁＝， x₂＝

又∵当x∈（－∞， ）时，>0；

当x∈（， ）时，<0；

当x∈（， ＋∞）时，>0．

∴x₁， x₂分别为f （x）的极大值与极小值点．

又∵；当时．

而f （）＝<0．

∴当x＝时，f （x）取得最小值．

（Ⅱ）f （x）在[－1， 1]上单调，则≥ 0（或≤ 0）在[－1， 1]上恒成立．

而＝[x²－2（a－1）x－2a]e^x， 令g（x）＝ x²－2（a－1）x－2a＝[x－（a－1）]²－（a²＋1）．

∴≥ 0（或≤ 0） 即g（x） ≥ 0（或≤ 0）．

当g（x） ≥ 0在[－1， 1]上恒成立时有：

①当－1≤ a－1 ≤1即0≤ a ≤2时， g（x）_min＝g（a－1）＝ －（a²＋1） ≥ 0（舍）；

②当a－1>1即a ≥ 2时， g（x）_min＝g（1）＝ 3－4a ≥ 0 ∴a≤（舍）．

当g（x） ≤ 0在[－1， 1]上恒成立时，有：

①当－1≤ a－1 ≤ 0即0≤ a ≤ 1时， g（x）_max＝g（1）＝3－4a ≤ 0， ∴≤ a ≤ 1；

②当0< a－1 ≤ 1即1< a ≤ 2时， g（x）_max＝g（－1）＝ －1 ≤ 0， ∴1< a ≤ 2；

③当1< a－1即a > 2时， g（x）_max＝g（－1）＝ －1 ≤ 0， ∴a >2．

故a∈[，＋∞）．