高考数学普通高等学校全国统一考试77

高考数学普通高等学校全国统一考试77

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页，第Ⅱ卷3至9页。考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷

注意事项：

1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。不能答在试题卷上。

3. 本卷共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　 　  球是表面积公式

　　　　　　　　　　　　 

如果事件A、Ｂ相互独立，那么　　　　　　　　　　  　　 其中R表示球的半径

　　　　　　　　　　　  球的体积公式

如果事件A在一次试验中发生的概率是P，那么　　　　　 

n次独立重复试验中恰好发生k次的概率　　　　　　  其中R表示球的半径

　

一、选择题

（１）函数的最小正周期是

（A）（B）（C）（D）

解：∵f(x)=sinx+cosx=sin(x+),∴T=,的最小正周期是π.选(C)

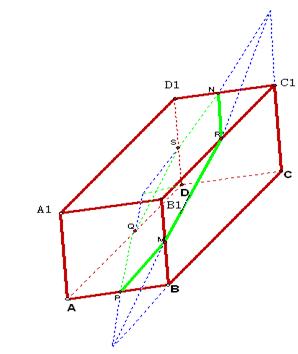
（２）正方体中，、、分别是、、的中点．那么，正方体的过、、的截面图形是

（A）　　　三角形（B）四边形（C）五边形（D）六边形

解：如图, 正方体的过、、的截面图形是六边形PMRSQ,选(D)

（３）函数的反函数是

（A）（B）

（C）（D）

解：由得,∴函数的反函数是y=,选(B)

（４）已知函数在内是减函数，则

（A）　　  ０＜≤１（B）－１≤＜０（C）≥１（D）≤－１

解：可用排除法,∵当ω>0时正切函数在其定义域内各长度为一个周期的连续区间内为增函数,∴排除(A)，(C),又当ω>1时正切函数的最小正周期长度小于π,∴在内不连续,在这个区间内不是减函数,这样排除(D),故选(B)。

（５）抛物线上一点的纵坐标为４，则点与抛物线焦点的距离为

（A）２　　（B）３

（C）４　　（D）５

解：这里,故点A与抛物线焦点的距离是4+1=5,选(D)

（６）双曲线的渐近线方程是

（A）（B）（C）（D）

解：在双曲线中将1改为0即得此双曲线的渐展程y=,选(C)

（７）如果数列是等差数列，即

（A）＋＋（B）＋＝＋

（C）＋＋（D）＝

解：因为对于等差数列{a_n}有：如果m,n,p,q都是非零的自然数,且m+n=p+q,则必有a_m+a_n=a_p+a_q,故选(B)

（８）的展开式中项的系数是

（A）840　 （B）－840　（C）210　　（D）－210

解：在通项公式T_k+1=中令k=4,即得展开式了x⁶y⁴项的系数840,选(A)

（９）已知点，，．设的平分线与相交于，那么有，其中等于

（A）　　  ２（B）（C）－３（D）－

解：由已知得,且1+λ<0,即,又∵∴-1-λ=2,∴λ=-3,选(C)

（10）已知集合，，则为

（A）或（B）或

（C）或　　　　（D）或

解：∵M=[-4,7],N=(-∞,-2)∪(3,+∞),∴M∩N={x-4≤x<-2或3<x≤+7},选(A)

（11）点在平面上作匀速直线运动，速度向量（即点的运动方向与相同，且每秒移动的距离为个单位）．设开始时点的坐标为（－10，10），则５秒后 点的坐标为

（A）（-2，4）（B）（-30，25）（C）（10，-5）（D）（5，-10）

解：设5秒后点P运动到点A,则,

∴=(10,-5),选(C)

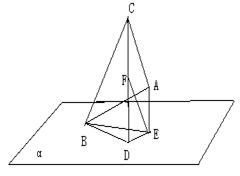
（12）的顶点B在平面内，、在的同一侧，、与所成的角分别是和．若＝３，＝，＝５，则与所成的角为

（A）（B）（C）（D）

解：如图，AE⊥平面α于E,CD⊥平面α于D,

EF∥AC,EF交CD于F,则∠ABE=30⁰,

∠CBD=45⁰,由此得CD=4,AE=1.5,∴EF=2.5,

而EF=AC=5 ∴∠FED=30⁰,即AC与平面

α所成的角为30⁰,∴选(C)

第Ⅱ卷

注意事项：

1．用钢笔或圆珠笔直接答在试题卷上

2．答卷前将密封线内的项目填写清楚

3．本卷共10小题，共90分

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上

（13）在和之间插入三个数，使这五个数成等比数列，则插入的三个数的乘积为_____．

解：a₁=,a₅=,a₂a₃a₄=(a₁a₅)^1.5=6³=216.

（14）圆心为(1,2)且与直线相切的圆的方程为_____________．

解：圆心(1,2)到直线5x-12y-7=0的距离r=,故所求的圆的方程为(x-1)²+(y-2)²=4

（15）在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被５整除的数共有_____________个．

解：不能被5整除的有两种情况：情况1、首位为5有种，情况2、首位不是5的有种，故在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被５整除的数共有+=192(个)．

（16）下面是关于三棱锥的四个命题：

①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．

②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．

③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥．

④侧棱与底面所成的角相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．

其中，真命题的编号是_____________．（写出所有真命题的编号）

解：正确的命题为①④

三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤

（17）（本小题满分12分）

已知为第二象限的角，，为第一象限的角，．求的值．

（18） （本小题满分12分）

甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.60，本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响．

（Ⅰ）前三局比赛甲队领先的概率；

（Ⅱ）本场比赛乙队以３：２取胜的概率．

（精确到0.001）

（19）（本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…．

（Ⅰ）证明为等比数列；

（Ⅱ）如果数列前３项的和等于，求数列的首项和公差．

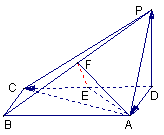
（20）（本小题满分12分）

如图，四棱锥中，底面为矩形，底面，，、分别为、的中点．

（Ⅰ）求证：平面；

（Ⅱ）设，求与平面所成的角的大小．

（21）（本小题满分14分）

设为实数，函数．

（Ⅰ）求的极值；

（Ⅱ）当在什么范围内取值时，曲线与轴仅有一个交点．

（22）（本小题满分12分）

、、、四点都在椭圆上，为椭圆在轴正半轴上的焦点．已知与共线，与共线，且．求四边形的面积的最小值和最大值．

参考答案

1-6: CDBBDC　7-12: BACACC

(2)分析：本题主要考查学生对截面图形的空间想像，以及用所学知识进行作图的能力，通过画图，可以得到这个截面与正方体的六个面都相交，所以截面为六边形，故选D.

13. 216;

14. .

分析：本题就是考查点到直线的距离公式，所求圆的半径就是圆心(1,2)到直线5x－12y－7=0的距离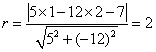：，再根据后面要学习的圆的标准方程，就容易得到圆的方程：

15. 192；　

16. ①，④

三．解答题：（共74分）

（17）（本小题满分12分）

已知为第二象限的角，，为第一象限的角，．求的值．

解：∵α为第二象限角, sinα=，∴cosα= -, tanα= -, tan2α= -.

又∵β为第一象限角, cosβ=, ∴sinβ=, tanβ=.

∴=.

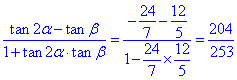（18）（本小题满分12分）

甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.60，本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响．

（Ⅰ）前三局比赛甲队领先的概率；

（Ⅱ）本场比赛乙队以３：２取胜的概率．

（精确到0.001）

解：⑴前三局比赛甲队领先分为两种情况：

①前三局比赛中甲队全部获胜，其概率为P₁==0.216；

②前三局比赛中甲队两局获胜、一局失败，其概率为P₂==0.432.

故前三局比赛甲队领先的概率为：P=P₁+P₂=0.648

⑵本场比赛乙队以３：２取胜，则乙队在前四局比赛中乙队获胜两局、在第五局比赛中获胜，其概率为P==0.13824≈0.138.

（19）（本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…．

（Ⅰ）证明为等比数列；

（Ⅱ）如果数列前３项的和等于，求数列的首项和公差．

⑴证明：设{a_n}中首项为a₁，公差为d.

∵lga₁,lga₂,lga₄成等差数列　∴2lga₂=lga₁·lga₄ ∴a₂²=a₁·a₄.

即(a₁+d)²=a₁(a₁+3d)　 ∴d=0或d=a₁.

当d=0时, a_n=a₁, b_n=, ∴，∴为等比数列；

当d=a₁时, a_n=na₁ ,b_n=，∴，∴为等比数列.

综上可知为等比数列.

⑵当d=0时, b_n=, ∴b₁+b₂+b₃== ∴a₁=；

当d=a₁时, b_n= ∴b₁+b₂+b₃= ∴a₁=3.

综上可知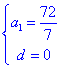 或 .

（20）（本小题满分12分）

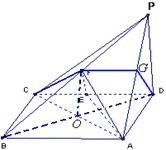
如图，四棱锥中，底面为矩形，底面，，、分别为、的中点．

（Ⅰ）求证：平面；

（Ⅱ）设，求与平面所成的角的大小．

解：⑴取PA中点G, 连结FG, DG.

 

.

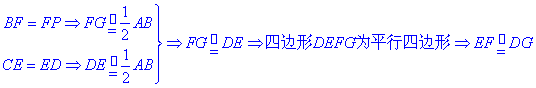
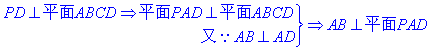
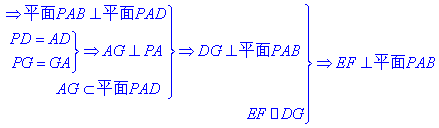⑵设AC, BD交于O，连结FO.

.

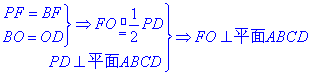设BC=a, 则AB=a, ∴PA=a, DG=a=EF, ∴PB=2a, AF=a.

设C到平面AEF的距离为h.

∵V_C-AEF=V_F-ACE, ∴. 即　∴. ∴AC与平面AEF所成角的正弦值为.

即AC与平面AEF所成角为.

（21）（本小题满分14分）

设为实数，函数．

（Ⅰ）求的极值；

（Ⅱ）当在什么范围内取值时，曲线与轴仅有一个交点．

解：⑴令得：.

又∵当x∈(-∞, )时, >0; 当x∈(,1)时, <0; 当x∈(1,+∞)时, >0.∴与分别为的极大值与极小值点.

∴_极大值=;　_极小值=.

⑵∵在(-∞, )上单调递增, ∴当时,;

又在(1,+∞)单调递增， 当时, .

∴当_极大值<0或_极小值>0时，曲线与x轴仅有一个交点.

即或>0,　∴a∈(-∞, )∪(1,+∞)

（22）（本小题满分12分）

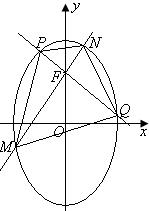
、、、四点都在椭圆上，为椭圆在轴正半轴上的焦点．已知与共线，与共线，且．求四边形的面积的最小值和最大值．

解：∵. 即.

当MN或PQ中有一条直线垂直于x轴时，另一条直线必垂直于y轴. 不妨设MN⊥y轴，则PQ⊥x轴.

∵F(0, 1) ∴MN的方程为：y=1，PQ的方程为：x=0分别代入椭圆中得：MN=, PQ=2.

S_{四边形PMQN}=MN·PQ=××2=2.

当MN,PQ都不与坐标轴垂直时，设MN的方程为y=kx+1 (k≠0)，代入椭圆中得：(k²+2)x²+2kx-1=0,　∴x₁+x₂=, x₁·x₂=.

∴

同理可得：.

S_{四边形PMQN}=MN·PQ==

(当且仅当即时，取等号).

又S_{四边形PMQN} =，∴此时S_{四边形PMQN}.

综上可知：(S_{四边形PMQN} )_max=2,  (S_{四边形PMQN} )_min=.