高考数学普通高等学校招生全国统一考试9

高考数学普通高等学校招生全国统一考试9

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.

（1）直线关于x轴对称的直线方程为　　　　　　　　　　　　　　　　

（A）　　　　（B）　　　　　（C）　　　　（D）

（2）已知　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（A）　　　　　　　　　（B）－　　　　　　 （C）　　　　　　　　（D）－

（3）抛物线的准线方程是，则a的值为　　　　　　　　　　　　　　　　　　　　　

（A）　　　　　　　　　　（B）－　　　　　　　 （C）8　　　　　　　　　　 （D）－8

（4）等差数列{a _n}中，已知　　　　　　　　　　　　　

（A）48　　　　　　　　　　 （B）49　　　　　　　　　 （C）50　　　　　　　　　 （D）51

（5）双曲线虚轴的一个端点为M，两个焦点为F₁，F₂，F₁MF₂=120°则双曲线的离心率为

　　　 （A）　　　　　　　　（B）　　　　　　　　（C）　　　　　　　 （D）

（6）设函数的取值范围是　　　　　　　　　　　　　　　

（A）（－1，1）　　　　　　　　　　　　　　　　　　　（B）（—1，+∞）

　　　 （C）（－∞，－2）∪（0，+∞）　　　　　　（D）（－∞，－1）∪（1，+∞）

（7）已知　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 （A）　　　　　　　 （B）　　　　　　　（C）　　　　　　 （D）

（8）函数上的偶函数，则=　　　　　　　　　　　　　　　　

（A）0　　　　　　　　　　 （B）　　　　　　　　　（C） 　　　　　　　　（D）

（9）已知点的距离为1，则a=　　　　　　　　　　　　　　　

（A）　　　　　　　　（B）－　　　　　　 （C）　　　　　 （D）

（10）已知圆锥的底面半径为R，高为3R，它的内接圆柱的底面半径为R，该圆柱的全面积为　　　　　　　　　　　　　　

（A）　　　　　　 （B）　　　　　　（C）　　　　　　（D）

（11）已知长方形的四个顶点A（0，0），B（2，0），C（2，1）和D（0，1）一质点从AB的中点P₀沿与AB夹角为θ的方向射到BC上的点P₁后，依次反射到CD、DA和AB上的点P₂、P₃和P₄（入射角等于反射角）.若P₄与P₀重合，则tgθ=　　　　　　　　　　　

（A）　　　　　　　　 （B）　　　　　　　　　 （C）　　　　　　　　　（D）1

（12）一个四面体的所有棱长都为，四个顶点在同一球面上，则此球的表面积为　　

（A）　　　　　　　 （B）4　　　　　　　　 （C）　　　　　　（D）

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上.

（13）不等式的解集是　　　　.

（14）的系数是　　　　 .

（15）在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB²+AC²=BC²”

 拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面面积与底面面积间的关系，可以得出的正确结论是：“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则　　　　　　　　　　　　　 .”

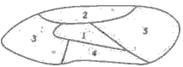
（16）如图，一个地区分为5个行政区域，现给地

图着色，要求相邻区域不得使用同一颜色，

现有4种颜色可供选择，则不同的着色方

法共有　　　　种.（以数字作答）

三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.

（17）（本小题满分12分）

　　　 已知正四棱柱ABCD—A₁B₁C₁D₁，AB=1，AA₁=2，点E为CC₁中点，点F为BD₁中点.

　　　 （I）证明EF为BD₁与CC₁的公垂线；

　　　 （II）求点D₁到面BDE的距离.

（18）（本小题满分12分）

　　　 已知复数z的辐角为60°，且z－1是z和z－2的等比中项，求z.

（19）（本小题满分12分）

　　　 已知数列满足

　　　 （I）求

　　　 （II）证明

（20）（本小题满分12分）

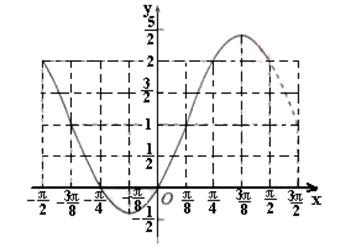
　　　　 已知函数.

　　　 （I）函数数的最小正周期和最大值;

　　　 （II）在给出的直角坐标系中，画出函数上的图象.

（21）（本小题满分12分）

　　　 在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南方向300km的海面P处，并以20km/h的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大问几小时后该城市开始受到台风的侵袭？

（22）（本小题满分14分）

　　　 已知常数在矩形ABCD中，AB=4，BC=4a，O为AB的中点，点E、F、G分别在BC、CD、DA上移动，且P为GE与OF的交点（如图），问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由.

数学（文史类）参考答案

一、选择题　　　　　　　　　

（1）C　　　（2）D　　 （3）B　　 （4）C　　　 （5）B　　　 （6）D　

（7）D　　　（8）C　　 （9）C　　 （10）B　　  （11）C　　　（12）A

二、填空题

（13）　 （14）　 （15）　　（16）72

三、解答题

（17）（I）证明：取BD中点M，连结MC，FM，

　　　  ∵F为BD₁中点， ∴FM∥D₁D且FM=D₁D

又EC=CC₁，且EC⊥MC，

∴四边形EFMC是矩形　∴EF⊥CC₁　

又CM⊥面DBD₁　∴EF⊥面DBD₁

∵BD₁面DBD₁，

∴EF⊥BD₁　故EF为BD₁与CC₁的公垂线

（II）解：连结ED₁，有V

由（I）知EF⊥面DBD₁，设点D₁到面BDE的距离为d，

则S_△DBC·d=S_△DCD·EF.

∵AA₁=2·AB=1.

故点D₁到平面BDE的距离为.

（18）解：设z=

　　　  由题设

　　　 即　

　　（舍去）

　　　 即z=

（19）（I）解∵

（II）证明：由已知

　　　

　　　　 =

　　　 　　所以

（20）解（I）

　　　　　　 　 

　　　 所以函数的最小正周期为π，最大值为.

（Ⅱ）由（Ⅰ）知

	1		1		1

故函数在区间上的图象是

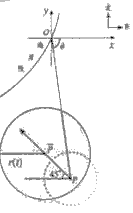
（21）解：如图建立坐标系：以O为原点，正东方向为x轴正向.

　　　　在时刻：t（h）台风中心的坐标为

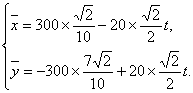
　　　　此时台风侵袭的区域是，

　　　　其中t+60，

　　　　若在t时，该城市O受到台风的侵袭，则有

即

即，　 解得.

答：12小时后该城市开始受到台风气侵袭

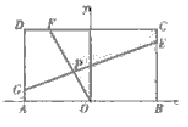
（22）解：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到定点距离的和为定值.

按题意有A（－2，0），B（2，0），C（2，4a），D（－2，4a）

设，

由此有E（2，4ak），F（2－4k，4a），G（－2，4a－4ak）.

直线OF的方程为：，　　　　①

直线GE的方程为：.　　②

从①，②消去参数k，得点P（x，y）坐标满足方程，

整理得.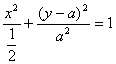

当时，点P的轨迹为圆弧，所以不存在符合题意的两点.

当时，点P轨迹为椭圆的一部分，点P到该椭圆焦点的距离的和为定长.

当时，点P到椭圆两个焦点的距离之和为定值.

当时，点P到椭圆两个焦点的距离之

和为定值.