高考数学高等学校招生全国统一考试24
本试卷分第I卷(选择题)和第II卷(非选择题)两部分. 共150分. 考试时间120分钟.
第I卷
参考公式:
 如果事件A、B互斥,那么
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么
n次独立重复试验中恰好发生k次的概率
Pn(k)=C![]() Pk(1-P)n-k
Pk(1-P)n-k
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知集合![]() (A){
(A){![]() } (B){
} (B){![]() }
}
(C){![]() } (D) {
} (D) {![]() }
}
(2)![]()
(A)![]() (B)1 (C)
(B)1 (C)![]() (D)
(D)![]()
(3)设复数![]() =
=
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)已知圆C与圆![]() 关于直线
关于直线![]() 对称,则圆C的方程为 (A)
对称,则圆C的方程为 (A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(5)已知函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 可以是 (A)
可以是 (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)函数![]() 的图象
的图象
(A)与![]() 的图象关于y轴对称 (B)与
的图象关于y轴对称 (B)与![]() 的图象关于坐标原点对称
的图象关于坐标原点对称
(C)与![]() 的图象关于
的图象关于![]() 轴对称 (D)与
轴对称 (D)与![]() 的图象关于坐标原点对称
的图象关于坐标原点对称
(7)已知球O的半径为1,A、B、C三点都在球面上,且每两点间的球面距离均为![]() ,则
,则
球心O到平面ABC的距离为 (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(8)在坐标平面内,与点A(1,2)距离为1,且与点B(3,1)距离为2的直线共有
(A)1条 (B)2条 (C)3条 (D)4条
(9)已知平面上直线l的方向向量e=![]() 点O(0,0)和A(1,-2)在l上的射影分别是O′和A′,则
点O(0,0)和A(1,-2)在l上的射影分别是O′和A′,则![]() e,其中
e,其中![]() =
=
(A)![]() (B)
(B)![]() (C)2 (D)-2
(C)2 (D)-2
(10)函数![]() 在下面哪个区间内是增函数
在下面哪个区间内是增函数
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)函数![]() 的最小正周期为 (A)
的最小正周期为 (A)![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2![]()
(12)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有
(A)56个 (B)57个 (C)58个 (D)60个
第Ⅱ卷
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
|
(14)设![]() 满足约束条件:
满足约束条件:
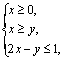
则![]() 的最大值是 .
的最大值是 .
(15)设中心在原点的椭圆与双曲线![]() =1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是
.
=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是
.
(16)下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱
③若四个侧面两两全等,则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱
其中,真命题的编号是 (写出所有正确结论的编号).
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知锐角三角形ABC中,![]()
(Ⅰ)求证:![]() ;
;
(Ⅱ)设AB=3,求AB边上的高.
(18)(本小题满分12分)
已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支.
求:(Ⅰ)A、B两组中有一组恰有两支弱队的概率;
(Ⅱ)A组中至少有两支弱队的概率.
(19)(本小题满分12分)
数列![]() 的前n项和记为Sn,已知
的前n项和记为Sn,已知![]() 证明:
证明:
(Ⅰ)数列![]() 是等比数列;
是等比数列;
(Ⅱ)![]()
(20)(本小题满分12分)
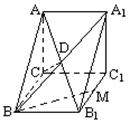
|
(Ⅰ)求证CD⊥平面BDM;
(Ⅱ)求面B1BD与面CBD所成二面角的大小.
(21)(本小题满分12分)
给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点。
(Ⅰ)设l的斜率为1,求![]() 与
与![]() 的夹角的大小;
的夹角的大小;
(Ⅱ)设![]() ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
(22)(本小题满分14分)
已知函数f(x)=ln(1+x)-x,g(x)=xlnx.
(Ⅰ)求函数f(x)的最大值;
(Ⅱ)设0<a<b,证明0<g(a)+g(b)-2g(![]() )<(b-a)ln2.
)<(b-a)ln2.
高考数学高等学校招生全国统一考试24
一.选择题
(1)C (2)A (3)C (4)C (5)A (6)D
(7)B (8)B (9)D (10)B (11)B (12)C
二.填空题
(13)0.1,0.6,0.3 (14)5 (15)![]() (16)②④
(16)②④
三.解答题
(17)本小题主要考查等差、等比数列的概念和性质,考查运算能力,满分12分.
本小题主要考查三角函数概念,两角和、差的三角函数值以及应用、分析和计算能力,
满分12分.
(Ⅰ)证明:![]()
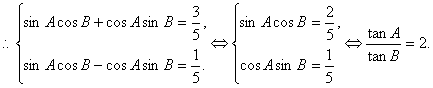
所以![]()
(Ⅱ)解:![]() ,
,![]()
即![]() ,将
,将![]() 代入上式并整理得
代入上式并整理得
![]()
解得![]() ,舍去负值得
,舍去负值得![]() ,
,
![]() 设AB边上的高为CD.
设AB边上的高为CD.
则AB=AD+DB=![]()
由AB=3,得CD=2+![]() . 所以AB边上的高等于2+
. 所以AB边上的高等于2+![]() .
.
(18)本小题主要考查组合、概率等基本概念,相互独立事件和互斥事件等概率的计算,运用数学知识解决问题的能力,满分12分.
(Ⅰ)解法一:三支弱队在同一组的概率为 ![]()
故有一组恰有两支弱队的概率为![]()
解法二:有一组恰有两支弱队的概率![]()
(Ⅱ)解法一:A组中至少有两支弱队的概率 ![]()
解法二:A、B两组有一组至少有两支弱队的概率为1,由于对A组和B组来说,至少有两支弱队的概率是相同的,所以A组中至少有两支弱队的概率为![]()
(19)本小题主要考查数列、等比数列的概念和性质,分析和推理能力,满分12分。
证明:(Ⅰ)∵![]()
∴ ![]() 整理得
整理得 ![]()
所以 ![]() 故
故![]() 是以2为公比 的等比数列.
是以2为公比 的等比数列.
(Ⅱ)由(Ⅰ)知![]() 于是
于是 ![]()
又 ![]() 故
故 ![]()
因此对于任意正整数 ![]() 都有
都有![]()
|
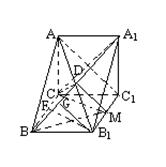
解法一:(Ⅰ)如图,连结CA1、AC1、CM,则CA1=![]()
∵CB=CA1=![]() ,∴△CBA1为等腰三角形,
,∴△CBA1为等腰三角形,
又知D为其底边A1B的中点,
∴CD⊥A1B. ∵A1C1=1,C1B1=![]() ,∴A1B1=
,∴A1B1=![]()
又BB1=1,A1B=2. ∵△A1CB为直角三角形,D为A1B的中点,
∴CD=![]() A1B=1,CD=CC1,又DM=
A1B=1,CD=CC1,又DM=![]() AC1=
AC1=![]() ,DM=C1M.
,DM=C1M.
∴△CDM≌△CC1M,∠CDM=∠CC1M=90°,即CD⊥DM.
因为A1B、DM为平在BDM内两条相交直线,所以CD⊥平面BDM.
(Ⅱ)设F、G分别为BC、BD的中点,连结B1G、FG、B1F,则FG//CD,FG=![]() CD.
CD.
∴FG=![]() ,FG⊥BD.
,FG⊥BD.
由侧面矩形BB1A1A的对角线的交点为D知BD=B1D=![]() A1B=1,
A1B=1,
所以△BB1D是边长为1的正三角形.
于是B1G⊥BD,B1G=![]() ∴∠B1GF是所求二面角的平面角,
∴∠B1GF是所求二面角的平面角,
又 B1F2=B1B2+BF2=1+(![]() =
=![]() ,
,
∴ 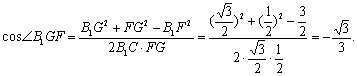
|
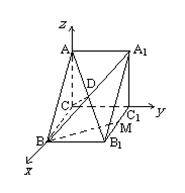
解法二:如图,以C为原点建立坐标系.
(Ⅰ)B(![]() ,0,0),B1(
,0,0),B1(![]() ,1,0),A1(0,1,1),
,1,0),A1(0,1,1),
D(![]() ,M(
,M(![]() ,1,0),
,1,0),
![]()
则![]() ∴CD⊥A1B,CD⊥DM.
∴CD⊥A1B,CD⊥DM.
因为A1B、DM为平面BDM内两条相交直线,所以CD⊥平面BDM.
(Ⅱ)设BD中点为G,连结B1G,则
G(![]() ),
),![]() 、
、![]() 、
、![]() ),
),![]()
![]()
![]()
所以所求的二面角等于![]()
(21)本小题主要考查抛物线的性质,直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力。满分12分。
解:(Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为![]()
将![]() 代入方程
代入方程![]() ,并整理得
,并整理得 ![]()
设![]() 则有
则有 ![]()
![]()
![]()
![]()
所以![]() 夹角的大小为
夹角的大小为![]()
(Ⅱ)由题设![]() 得
得 ![]()
|
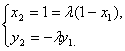
由②得![]() , ∵
, ∵ ![]() ∴
∴![]() ③
③
联立①、③解得![]() ,依题意有
,依题意有![]()
∴![]() 又F(1,0),得直线l方程为
又F(1,0),得直线l方程为
![]()
当![]() 时,l在方程y轴上的截距为
时,l在方程y轴上的截距为![]()
由 ![]() 可知
可知![]() 在[4,9]上是递减的,
在[4,9]上是递减的,
∴ ![]()
直线l在y轴上截距的变化范围为![]()
(22)本小题主要考查导数的基本性质和应用、对数函数性质和平均值不等式等知识以及综合推理论证的能力,满分14分.
(Ⅰ)解:函数![]() 的定义域为
的定义域为![]() .
.
![]() 令
令 ![]()
当![]() 当
当![]() 又
又![]()
故当且仅当x=0时,![]() 取得最大值,最大值为0.
取得最大值,最大值为0.
(Ⅱ)证法一:![]()
![]()
由(Ⅰ)结论知![]()
由题设 ![]()
因此 ![]()
![]()
所以 ![]()
又![]()
综上 ![]()
证法二:![]()
设![]()
则 ![]()
当![]() 在此
在此![]() 内为减函数.
内为减函数.
当![]() 上为增函数.
上为增函数.
从而,当![]() 有极小值
有极小值![]()
因此 ![]() 即
即 ![]()
设 ![]()
则 ![]()
当![]() 因此
因此![]() 上为减函数.
上为减函数.
因为 ![]()
即 ![]()