第一学期高三数学复习测试（三）函 数
（时间：90分钟 满分：150分）
班 级______________ 学 号________ 姓 名________________ 得 分_______________
一、填空题(4分
12
48分)
1．函数
的定义域为_____________________________。
2. 若
的定义域是
，则
的定义域是______________________。
3．函数
的定义域
，则其值域是____________________________。
4．已知
，则
___________。
5. 函数
（
）的反函数是___________________________。
6．函数
的递减区间是________________________。
7．若
，则不等式
的解集是___________________________。
8．已知偶函数
在
上是减函数，若
，则
的取值范围是___________。
9. 若定义在区间
上的函数
是奇函数，则
________。
10．设是
上的周期为2的偶函数，已知当
时，
，则当
时，
_________________________。
11．设两个命题：①关于的不等式
的解集是，②函数
是减函数。若这两个命题中有且只有一个真命题，则实数
的取值范围是_______________________。
12．对于定义在R上的函数，有下述四个命题：
①若是奇函数，则
的图象关于点
对称；
②若对x
R，有
，则
的图象关于直线
对称；
③若函数的图象关于直线对称，则为偶函数；
④函数
与函数
的图象关于直线对称。
其中正确命题的序号为____________________________（把你认为正确命题的序号都填上）。
二、选择题(4分416分)
13．函数
的图象如图，其中a、b为常数，则下列结论正确的是…………（ ）
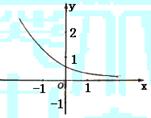A．
B．
C．
D．
14．函数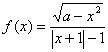
为奇函数的充要条件是…………………………………………（ ）
A．
B．
C．
D．
15．下列函数中有反函数的是…………………………………………………………………（ ）
A．
B．
C．
D．
16．若函数
，则该函数在
上是……………………………………（ ）
A．单调递减无最小值 B．单调递减有最小值
C．单调递增无最大值 D．单调递增有最大值
三、解答题（本大题共86分）
17. (10分)已知
，求
的最小值。
18．(12分) 已知函数
。
（1）当
时，求函数
的最大值与最小值；
（2）求实数
的取值范围，使
在区间
上是单调函数。
19．(14分) 已知
，
，设
，
若
的最大值为
，求
的值。
20．(16分) 已知函数
（
为常数）且方程
有两个实根为
。
（1）求函数的解析式；（2）设
，解关于的不等式：
。
21．(16分)某游艺场每天的盈利额
（单位：元）与售出的门票数（单位：张）之间的函数关系如图，试分析图形求：
（1）的函数关系式；
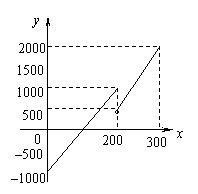（2）要使该游艺场每天的赢利额超过1000元，那么每天至少应售出多少张门票？
22.(18分)函数
的定义域为
（
为实数）。
（1）当
时，求函数
的值域；
（2）若函数在定义域上是减函数，求的取值范围。