第一学期期末质量抽测高三数学理科试卷
| 题号 | 1至12 | 13至16 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
一、填空题（每小题4分，共48分）
1．已知集合
，
，若
，则实数m= 。
2．
。
3．函数
的最小正周期为 。
4．若
的二项展开式中含
的系数是80，则实数
的值为 。
5．设函数
，则方程
解的个数为 。
6．在极坐标系中，O是极点，设点
，
，则
。
7．无穷数列{an}中，
，则a2+a4+a6+…+a2n+…= 。
8．函数
的反函数
的图象与y轴交于点P（0，2），则方程
的根是x= 。
9．从1，2，3，4，5，6，7，8中任取三个数，能组成等差数列的概率是 。
10．函数
在（1，+¥）上单调递增，则实数p的取值范围是
。
11．数列
中，
，若对任意的正整数n，
都成立，
| 学校 | 文科均分 | 理科均分 |
| 学校A | 101.4 | 103.2 |
| 学校B | 101.5 | 103.4 |
则k的取值范围为 。
12．右面是某次测验成绩统计表中的部分数据。
某甲说，B校文理平均分都比A校高，全体学生的
平均分肯定比A校的高；
某乙说，两个学校平均分不一样，全体学生的平均分可以相等；
某丙说，A校全体学生的平均分可以比B校的高。
你同意他们的观点吗？我不同意 的观点，请举例
。
二、选择题（每小题4分，共16分）
13．设z是复数，以下命题中错误的是 （ ）
（A）z为实数的充分必要条件是
；
（B）z为实数的充分必要条件是
；
（C）z为纯虚数的充分必要条件是
；
（D）z为纯虚数的充分必要条件是
。
14．函数
，（0＜＜1，-1＜
＜0）的图象为 （ ）
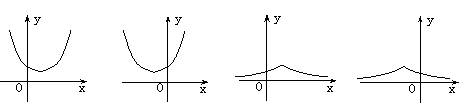
（A） （B） （C） （D）
15．设
是定义在R上的函数，给出下列命题： （ ）
①若存在x1、x2ÎR，x1＜x2，使
<
成立，则函数在R上单调递增；
②若存在x1、x2ÎR，x1＜x2，使
成立，则函数在R上不可能单
调递减；
③若存在x2＞0，对任意x1ÎR，都有<
成立，则函数在R上单
调递增；
④对任意x1、x2ÎR，x1＜x2，都有
成立，则函数在R上单调递减。
以上命题正确的序号是
（A）①③； （B）②③； （C）②④； （D）②。
16．记数列前
项的积为
，设
。若数列
，为正整数。则使
最大的的值为 （ ）
（A）11； （B）22； （C）25； （D）48。
三、解答题（满分86分）
17．（本满分12分）
已知a为锐角，
，b是第四象限有角，
，求
的值。
解：
18．（本满分12分，第（1）题4分，第（2）题8分）
Z为一元二次方程
的一个根，且
。
（1）求复数z；
（2）若实数满足
≤
，求的取值范围。
解：
19．（本满分14分，第（1）题8分，第（2）题6分）
据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈
的模型波动（
为月份），已知3月份达到最高价8千元，7月份价格最低为4千元，该商品每件的售价为
（为月份），且满足
。
（1）分别写出该商品每件的出厂价函数、售价函数的解析式；
（2）问哪几个月盈利？
解：
20．（本满分14分，第（1）题4分，第（2）题10分）
已知函数
的图像与轴正半轴的交点为
。
（1）求数列的通项公式；
（2）令
（为正整数），问是否存在非零整数
，使得对任
意正整数，都有
？若存在，求出的值，若不存在，请说明理由。
解：
21．（本满分16分，第（1）题4分，第（2）题7分，第（3）题5分）
已知函数
，
（1）求
的值；
（2）猜测函数的图像具备怎样的对称性，并给出证明。
（3）若函数的图像与直线
及轴所围成的封闭图形的面积为S，
求S的值。
解：
22．（本满分18分，第（1）题4分，第（2）题6分，第（3）题8分）
（1）若等比数列的前项和为
，求实数的值；
（2）对于非常数数列有下面的结论：若数列为等比数列，则该数列的前项
和为
(
、
为常数)。写出它的逆命题并判断真假，请说明理由。
（3）若数列为等差数列，则该数列的前项和为
。对其逆命题进行
研究，写出你的结论，并说明理由。
解：