第一学期期中考试数学试题2

第一学期期中考试数学试题2

命题人：郭立效　 审核人：曹志仕

2006．11．10

第一部分(选择题)

一、选择题 (5分×10=50分)

1、集合A={xx²－4=0}，B={x ax－2=0}，若A∪B=A，则实数a的值为

A.1　　　　　　　　　B. －1　　　　　 　　 C. －1或1　　　　　 D. －1或0，或1

2、函数y=的定义域是

A.[ －,－1)∪(1,]　　 　　　　 B.(－,－1)∪(1, )

C.[－2, －1)∪(1， 2]　　　　　　　　　　　　　D.(－2,－1)∪(1，2)

3、函数f(x)=xx+a+b是奇函数的充要条件是

A.ab=0　　　　　　　　　　　　　 B.a+b=0

C.a=b　　　　　　　　　　　　　　　　　 D.a²+b²=0

4、5名身高互不相等的学生站成一排照像，要求从中间向两边身高依次降低，共有站法

A.10种　　　　　　　　　 B.8种　　　　　　　　　 C.6种　　　　　　D.以上都不对

5、等差数列{a_n}的前n项和记为Sn，若a₃+a₈+a₁₃为一个确定的常数，则下列各数中也是常数的是

A.S₆　　　　　　　　　　　 B.S₈　　　　　　　　　　　C.S₁₁　　　　　　 D.S₁₅

6、同时投掷大小不同的两颗骰子，所得点数之和是5的概率是

A.　　　　　　  B.　　　　　 C.　　　 D.

7、f(x)是定义在[－C,C]上的奇函数，其图象如下，

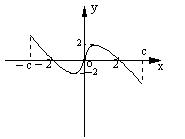令g(x)=af(x)+b，则下列关于函数g(x)的

叙述正确的是

A.若a<0,则函数g(x)的图象关于原点对称

B.若a=－1, －2<b<0，则方程g(x)=0有大于2的根

C.若a≠0，b=2，则方程g(x)=0有两个实根

D.若a≥1，b<2，则方程g(x)=0有三个实根

8、已知关于x的方程x²+xcosAcosB－2=0的两根之和是两根之积的一半,则△ABC一定是

A.直角三角形　　　　 B.钝角三角形　　　　

C.等腰三角形　　　　 D.等边三角形

9、设m,n是两条不同的直线，α、β、γ是三个不同的平面，给出下列四个命题

①若m//α,n//α,则m//n；

②若m⊥α,n∥α，则m⊥n；

③若α∥β, β∥γ,m⊥α,则m⊥γ；

④若α⊥γ，β⊥γ，则α⊥β；

其中真命题的序号是

A.①②　　　　　　　　　　　　　 B.②③　　　　　　　　　

C.③④　　　　　　　　　　　　　 D. ①④

10、对于实数x≥0，定义符号[x]表示不超过x的最大整数，则方程[2sinx]=[x]的解集为

A.[0，]∪(1，)　　　　　　　 B. (1, )∪(，2)

C.[0, )∪(1, )∪(，2)　　　 D. [0, )∪(1, )∪(，2)

二、填空题 (5分×6=30分)

11、已知f(x)=，f(lga)=，则a=　 ▲　　.

12、规定记号“×”表示两个正数间的一种运算：a×b=+a+b(a>0,b>0)，若1×k=3，则函数f(x)=k×x的值域是　 ▲　　.

13、在数列{a_n}中，a₁=15，3a_n+1=3a_n－2，n∈N*，则该数列中相邻两项的乘积是负数的两项积是　　▲　　 .（数字作答）。

14、正方体ABCD－A₁B₁C₁D₁中，E、F分别是AB、CC₁的中点，则异面直线A₁C与EF所成角的余弦值为　 ▲　　.

15、一家庭(父亲、母亲和若干小朋友)去某地旅游，甲旅行社说：“若父亲买全票一张，其余的人可享受半票优惠”，乙旅行社说：“家庭旅行算集体票，按原价的六折优惠。“这两家旅行社的原价是一样的，设家庭中的小朋友数为x，两家旅行社的收费分别为y_甲、y_乙，若y_甲<y_乙，则x的范围为　 ▲　 .

16、对于函数f(x)=cosx+sinx给出下列四个命题。

①存在α∈(0,),使f(α)= ；

②存在α∈(0,),，使f(x+α)=f(x+3α)

③存在α∈R，使f(x+α)的图象关于y轴对称；

④函数f(x)的图象关于点(,0)对称

其中正确的命题序号是　 ▲　　.

三、解答题 (12分+14分+14分+14分+16分=70分)

17、已知f(x)=cos⁴x－2sinxcosx－sin⁴x，

(1)求f(x)的最大值及取最大值时x的值。

(2)在直角坐标系中作出y=f(x)的一个周期的图象(用五点法)

18、已知双曲线C的两条渐近线过原点，且与以A(,0)为圆心，1为半径的圆都相切，双曲线C的一个顶点A′与A关于直y=x对称。

(1)求双曲线C的方程；

(2)过点(1，0)，以v= (1，k)为方向向量的直线l与双曲线C有公共点，求

k的范围。

19、函数f(x)=x²+ax+3，x∈[－2,2]

(1)若a=2，求f(x)的值域；

(2)若f(x)>a恒成立，求a的取值范围；

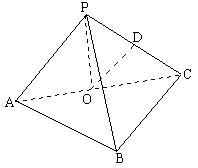
20、如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=mPA，点O、D分别是AC、PC的中点，OP⊥底面ABC，

(1)求证OD//平面PAB；

(2)当m=时，求直线PA与平面PBC所成角的正弦值；

(3)当O在平面PBC内的射影恰好为△PBC的重心时，求m的值。

21、已知x∈(n,n+1)，n∈N*，记函数f(x)=x(x+)的值是整数的个数为a_n.

(1)求数列{a_n}的通项公式；

(2)记b_n=() ·，求证：b₁+b₂+…+b_n<；

(3)令c_n=，其中a>0，a≠1，若{c_n}为递增数列，则求a的范围；

滨中、阜中高三联考2006-2007学年度第一学期期中考试

数　学　答　题　纸

题号	11-16	17	18	19	20	21	总  分
得分

二、填空题 (5分×6=30分)

11、_____________.　　　　　　12、_____________.　　　　　 13、_____________.

14、_____________.　　　　　 15、_____________.　　　　　 16、_____________.

三、解答题

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

18、(14分)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

	19、(14分)

座位号：_________

20、(14分)

　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

	21、(16分)