高级中学高考数学冲刺试题(一）
一．选择题：（每题5分）
1.已知函数f(x+4)的反函数图像过点（－1，－4），则函数f(x)的图像过点 （ ）
A．（0，－1） B．（―4，―1） C．（ 1，―4） D．（―1，―4）
2.把函数y=2x2－4x＋5的图像按向量
平移得到y=2x2的图像，且
,
=(－1,1), 
=4,则
=
( )
A．（－1，－3） B．（―3，―1） C．（ 1，―3） D．（―3，1）
3.若曲线f(x)=x4 －x＋2在点P处的切线与直线x＋3y－1=0垂直，则点P的坐标为（ ）
A．（ 1，0） B．（1，2） C．（ －1，4） D．（―1，0）
4. 若a、b
，则 
是
的（ ）条件
A．充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
5.种植两株不同的花卉，若它们的存活率分别是p或q，则恰有一株存活的概率为（ ）
A．p＋q－2pq B．p＋q－pq C．p＋q D．pq
6.已知首项为正数的等差数列
满足：
,
,则使前n项和
Sn>0成立的最大自然数n是 ( )
A．4009 B．4010 C．4011 D．4012
7.若函数f(x)=asinx＋2bcosx对任意实数x都有
,则直线
与直线
的夹角大小为
（ ）
A．actan3
B．actan 
C．actan
D．以上都不对
8.从四种不同的顔色中选取若干种顔色给正方体ABCD-A1B1C1D1的六个面涂色，要求相邻两个面涂不同的顔色，则共有涂色方法有
A．24种 B．72种 C．96种 D．48种 （ ）
9.定义在R上的周期函数
,若周期T=2，直线x=2是它的图像的一条对称轴，且 在[－3，－2]上是减函数，如果A、B是锐角三角形的两个内角，则
（ ）
A．
> 
B．>
C．> 
D．>
10. 已知
,方程
在区间（0，3）内的根的个数为
（ ）
A．0 B．1 C．2 D.3
二、填空题：（每题5分）
11、函数
的图像与函数
的图像关于____________________对称
12、若
的展开式的各项系数之和为－32,那么展开式中的常数项为_________.
13、不等式
恒成立，则
的取值范围是_________________
14、甲、乙两名篮球运动员，投篮的命中率分别为
，设甲投4球恰好投进3球的概率
为
，乙投3球恰好投进2球的概率为
，则与的大小关系为_____________
15、关于函数
，有下列命题：①其最小正周期是
；②其图象可由
向左平移
个单位得到；③其表达式可改写为
；
④在
上为增函数。其中正确的命题的序号是________________.
16、已知
，把数列
的各项排成三角形状：
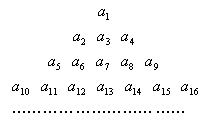记
表示第x 行中第y个数，则
_____.
三、解答题：（共70分）
17．已知向量
，向量
与向量
的夹角为
，且
。
（1）求向量。 （2）若
，其中A,C是
的
内角。若三角形的三个内角A,B,C依次成等差数列，试求
的取值范围。
18．质点M位于数轴的
处，质点N位于
处，质点M每隔1秒向左或向右移
动2个单位，质点M向左移动的概率为
，向右移动的概率为
，质点N每隔1秒
向左或向右移动1个单位，质点N向左移动的概率为，向右移动的概率为
。
（1）求3秒末，质点M在处的概率。
（2）求2秒末，质点M,N同时在处的概率。
19.已知
是函数
的一个极值点,其中,
（1）求
的关系式。（2）求的单调区间。
（3）当
时，函数
的图象上任一点的切线斜率恒大于3
，求的取
值范围。
20、如图，直三棱柱
中，
，
，侧棱
，侧面
的两条对角线交点为D，
的中点为M,
（1）求证：
（2）求面
所成角的大小。
 |
21．已知正项数列
，满足
（1）求证：
（2）求证：