高级中学高三年级第六次阶段考试数学试卷
注意：
1.本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分．考试时间120分钟．
2.请将第Ⅰ卷的答案和第Ⅱ卷的解答均填写在答题纸的对应地方，答在试题卷或草稿纸上不得分，考试结束时只交答案卷．
3.答题前请将答题纸上密封线内的有关项目填写清楚，密封线内不能答题．
第Ⅰ卷（选择题共50分）
参考公式：
如果事件
、
互斥，那么
如果事件、相互独立，那么
·
·
如果事件在一次试验中发生的概率是
，那么它在
次独立重复试验中恰好发生
次的概率
球的表面积公式
，其中
表示球的半径．
球的体积公式
，其中表示球的半径．
|
1．若
，则
的值为
（A）2
（B）
（C）1
（D）
2．对抛物线
，下列描述正确的是
（A）开口向上，焦点为
（B）开口向上，焦点为
（C）开口向右，焦点为
（D）开口向右，焦点为
3．函数
是
（A）奇函数且最大值为2 （B）偶函数且最大值为2
（C）奇函数且最大值为
（D）偶函数且最大值为
4．在数列
中，
，
，则
的值为
（A）49 （B）50 （C）51 （D）52
5．采用简单随机抽样，从含有6个个体的总体中抽取一个容量为3的样本，个体a前两次未被抽到，第三次被抽到的概率为
（A）
（B）
（C） 
（D）
6．函数
在区间
上存在
，使
，则
的取值范围是
（A）
（B）
（C）
（D）
7．下列说法正确的是
（A）若
，则
（B）等比数列是递增数列的一个必要条件是公比大于1
（C）
的否定是
（D）若
，则
或
8．某银行储蓄卡的密码是一个4位数，某人用千位、百位上的数字之积作为十位、个位上的数字(如2816)的方法设计密码，当积为一位数时，十位上数字选0，千位、百位上都能取0，这样设计出来的密码有
（A）90个 （B）99个 （C）100个 （D）112个
9．如果实数
满足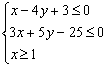
， 目标函数
的最大值为12, 最小值3, 那么实数
的值为
（A）
（B）2
（C）
（D）不存在
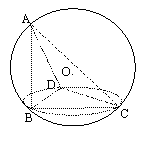10．如图，已知三棱锥A-BCD的所有顶点都在球O的表面上，且AC=
，其余棱长均为
，则球O的表面积为
（A）
（B）
（C）
（D）
第Ⅱ卷 (非选择题 共100分)
|
11．直线
与
是圆的两条切线，则该圆的面积是 。
12．海上有A、B两个小岛，相距10海里，从A岛望C岛和B岛成60º的视角，从B岛望C岛和A岛成75º的视角。则B、C间的距离是 海里.
13．已知定点
和圆
＋
＝4上的动点B，动点P满足
，则点P的轨迹方程为 ．
14．若
，且:
=3:1,那么
的展开式中系数最大的项是
.
15．已知函数
，若
，则
的取值范围是
.
16．已知空间三个平面
两两垂直，直线
与平面
所成的角都是
，则直线与平面
所成角的是
.
三、解答题：本大题共5小题，共70分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤。
17．（本小题满分12分）
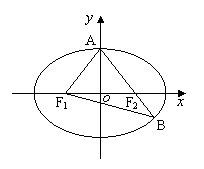如图，已知椭圆
，
分别为椭圆的左、右焦点，A为椭圆的上顶点，直线
交椭圆于另一点B。
（Ⅰ）若
，求椭圆的离心率；
（Ⅱ）若椭圆的焦距为2，且
，求椭圆的方程。
18．（本小题满分14分）
已知
（Ⅰ）求
；
（Ⅱ）若
，求
的取值范围。
19．（本小题满分14分）
如图，已知斜三棱柱
中，侧面
与底面垂直，且
.
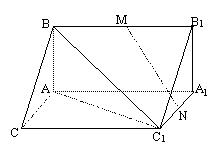
（Ⅰ）求证：
；
（Ⅱ）若N为
的中点，问侧棱
上是否存在
一点M，使
平面
成立，并说明理由；
（Ⅲ）求二面角
的大小（用反三角函数表示）
20．（本小题满分14分）
已知
,数列
满足
（Ⅰ）求证：数列
是等比数列；
（Ⅱ）当n取何值时，
取最大值，并求出最大值.
21．（本小题满分16分）
已知函数
的定义域为
，导数
满足0＜＜2 且
，常数
为方程
的实数根，常数
为方程
的实数根．
（Ⅰ）若对任意
，存在
，使等式
成立．试问：方程有几个实数根；
（Ⅱ）求证：当
时，总有
成立；
（Ⅲ）对任意
，若满足
，求证：
。