高考专题复习——不等式
第一节 不等式的性质
一、 重点难点剖析
1、正确理解不等式的概念：
a-b>0Ûa>b
a-b=0Ûa=b
a-b<0Ûa<b
2、不等式的性质包括基本性质和运算性质两部分
(1)基本性质：a>bÛb>a;
a>b,b>cÛa>c;
a>bÛa+c>b+c;
c>0时，a>bÛac>bc;
c<0时，a>bÛac<bc.
(2)运算性质：a>b,c>dÞa+c>b+d;
a>b,c<dÞa-c>b-d;
a>b>0,c>d>0Þac>bd;
a>b>0,c>d>0Þ>
a>b>0Þan>bn (nÎN且n>1);
a>b>0Þ > (nÎN且n>1).
上述性质中，条件与结论的逻辑关系有两种：推出关系“Þ”和等价关系“Û”，要注意区别．一般地，证明不等式时，进行的是一系列推出变换；解不等式时，进行的是一系列等价变换．不等式的概念和性质是进行变换、证明不等式和解不等式的依据．
二、 例题讲解：
例1 若a,b是任意实数，且a>b，则（ ）．
（A）a2>b2 （B）<1 （C）lg(a-b)>0 （D）
例2 已知都是实数，给出下列命题；
①ac2>bc2Ûa>b
②
③(x-a)(x-b)£0Û
④
其中正确命题的个数是（ ）．
（A）1 （B）2 （C）3 （D）4
例3 设a,b是不相等的正数， 
，
，
，
．试比较A、G、H、Q的大小．
例4 船在流水中在甲地和乙地间来回行驶一次的平均速度和船在静水中的速度是否相等，为什么？
三、 习题
（1）若a>b>c，则一定成立的不等式是（ ）．
（A）ac>bc （B）ab>ac
（C）a-c>b-c （D）a-c<b-c
（2）若x<a<0，则一定成立的不等式是（ ）．
（A）x2<ax<a2 （B）x2>ax>a2
（C）x2<a2<ax （D）x2>a2>ax
（3）a,bÎR，下列命题中的真命题是（ ）．
（A）若a>b，则a>b （B）若a>b，则
（C）若a>b，则a3>b3
（D）若a>b，则
（4）设a,b是满足ab<0的实数，则（ ）．
（A）a+b<a-b （B）a+b>a-b
（C）a-b<a-b （D）a-b<a+b
（5）以下四个不等式：¬a<0<b；b<a<0；® b<0<a；¯0<b<a，其中使成立的充分条件有（ ）．
（A）1个 （B）2个 （C）3个 （D）4个
（6）已知a<b，化简a-b-3-b-a+2=_______
（7）已知a>b>c>d>0，且
则e,f的大小关系是_____________
（8）已知
，则a,b,0,1的大小顺序是________
（9）x>y或
同时成立的充要条件是_______________
（10）已知a,b为不等正数，s<t<0，
则u,v的大小关系是 ________________
（11）已知-1<2a<0，将下列各数按照从小到大的顺序排列，并说明理由．
（12）已知a为正数，
，试比较
四个数的大小．
第二节 不等式的解法
一、重点难点
不等式解法，包括一元一次不等式（组）、一元二次不等式（组）、分式不等式、高次不等式等有理不等式，简单的无理不等式、指数不等式、对数不等式以及含有绝对值符号的不等式的求解和解集的确定．
1、形如ax+b>0和ax2+bx+c>0(<0)(a¹0)的不等式（组）的解法和解集的确定要熟练掌握．它们是解各种类型不等式的基础．高次不等式的解法是通过因式分解，将它化为一次或二次因式的乘积，然后用“序轴标根法”求解集．解有理分式不等式时，一般先通过移项，把一边化为零，另一边化为因式之积或商，再等价转化为高次不等式解之．
2、解无理不等式时，通常转化为有理不等式组求解．常见的转化有：
(1)
(2) 
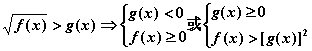
(3) 
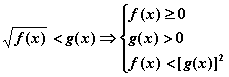
此外还可以通过换元法、图象法等．
3、解含有绝对值符号的不等式关键是正确地脱去绝对值符号，转化为有理不等式再求解，常见的转化有：
(1)f(x)<g(x) (g(x)>0)Û-g(x)<f(x)<g(x)
(2) f(x)>g(x) (g(x)>0)Ûf(x)<-g(x)或f(x)>g(x)
(3) f(x)<g(x)Û f2(x)<g2(x)
或f(x)>g(x)Û [f(x)+g(x)][ f(x)-g(x)]>0
含有多个绝对值的不等式，可采用“零点分区间”法求解．利用绝对值的几何意义解含有绝对值符号的不等式，也是一种简便的方法．此外，借助函数图象也是一种好方法．
4、解简单的指数、对数不等式时，常用的方法有同底法、转化法、换元法和图象法等．
同底法：将指数、对数不等式转化为相同的底数后，再根据函数单调性进行同解变形。
转化时，不要疏忽了对定义域的要求。
换元法：多用于两边是和的形式，把原不等式换元成一元二次不等式或无理不等式等形式，或先两边取对数后换元，要注意取对数时其数必须为正，要注意新元的取值范围．
转化法：多用于指数不等式，通常对不等式两边取同底对数，转化为对数不等式．要注意转化的等价性．
二、例题讲解：
例1
已知全集I=R，集合
，
，
（1）试求实数a的取值范围，使
；
（2）试求实数的取值范围，使
．
例2
解下列不等式：
注意：这是一组解简单的高次不等式的问题，采用的解法叫做数轴标根法，图中所画的曲线实际上是函数f(x)=(x-x1)(x-x2)…(x-xn)的图象的示意图这一过程中，应当注意两点：（1）最右边的一个区间上，函数图象位于x轴的上方；（2）当相应的方程有偶次重根时，图像与x轴相切．
例3 设a¹b，解关于的不等式：
注意：解含字母系数的不等式，要有对字母作分类讨论的准备，但讨论什么，怎么讨论要在求解过程中看等价变形的要求去定，也可能不必讨论．
例4 解不等式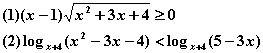
例5 解关于x的不等式
例6 解不等式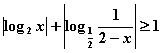
注意：化去不等式中的绝对值号转化为不含绝对值号的不等式是此类问题的通常思路，这就要确定log2x，log2(2-x)取正号或负号的条件，而其中对x作分类讨论的全集又是由x>0，且2-x>0，决定的．
例7
解关于x的不等式：
三、习题
1．下列不等式中，与不等式
同解的是（
）．
A．(x-3)(2-x)³0 B．(x-3)(2-x)>0
C．
D．lg(x-2)£0
2．关于x的不等式x2>a2与下列不等式中的（ ）等价．
A．x>a B．x>a
C．x>a或x<-a D．x>a或x<-a
3．下列不等式中解集是Æ的是（ ）
A. 4x2-4x+1£0 B.4x2-4x-1£0
C. 4x2-4x+2£0 D．4x2-4x-2£0
4．不等式
的解集为（
）．
A．R
B．
C．
D．
5．设
，则M等于（
）
A．
B．
C．
D．
6．不等式
的解集为（
）．
A．
B．
C．
D．
7．不等式(1-x)(1+x)>0的解集为（ ）．
A．(1,-1) B．(-¥,-1)È(-1,1)
C．(-¥,-1)È( 1,+¥) D．(-¥,-1)
8．不等式x+2+x-1<4的解集为（ ）．
A．(-2,1)
B．[-2,1] C．
D．
9. 在下列各题的空格上填写相应不等式的解集
(1) x2-x+6>0 ______________
(2) 2x2-3x-2<0 ______________
(3) 1-x-x2£0 ______________
(4) x2+x+3³0 ______________
(5)
______________
(6) x2-2x+4<0 ______________
(7)
______________
(8) x2(x2-1)(x+3)³0 _____________
(9)
_____________
(10)
_____________
10. 解下列不等式
第三节 不等式的证明
一、重点难点
不等式证明的重点是复习、体会、运用证明中常用的几种方法．这些方法是比较法，综合法，分析法，以及反证法，数学归纳法等．有时也要涉及一点放缩法，但不要去追求那些特殊的放缩技巧．
1、比较法有两种途径，即作差法和作商法，
作差法的基本步骤是作差--变形--定号（正负号）．变形是关键，通常将差式因式分解成积的形式或完全平方式与完全平方式（正数）和的形式，它是定号的依据，尤其适用具有多项式结构特征的不等式的证明，即A-B>0ÛA>B。
求商比较法的步骤是做商--变形--判断（与1比大小），即
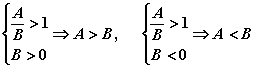
比商法适用具有乘积形式结构特征的不等式的证明。
2、综合法的重点是正确运用有关基本不等式，即
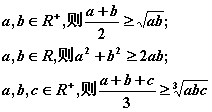
以及它们的变形形式:
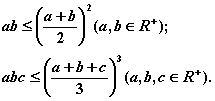
注意上述式子等号成立的条件。
还有含绝对值符号的不等式的性质:
分析法（执果索因）和综合法（持因导果）不仅是不等式证明中常用的方法，也是十分重要的逻辑思维方法．它对于指导我们认识条件和结论之间的联系，设计适当的推演步骤、运算方案，使问题得到解决，起着很大的作用．
3、反证法和数学归纳法都是只在特定情况下才采用的证明方法．
二、例题讲解：
例1 已知a,bÎR，求证：
．
例2 已知a,b,c均为正数，求证
分析:由于所证不等式两端都是幂和积的形式，且a,b,c为正数，可选用商值比较法.
例3 已知a,b,cÎR，
求证：
．
分析: 不等式的左端是根式，而右端是整式，应设法通过适当的放缩变换将左式各根式的被开方式转化为完全平方式．
例4 设a+b>0，求证：
分析: 当所证结论在形式上比较繁杂时，一般都可采用分析法.
例5 已知a,b,c都是正数，
求证：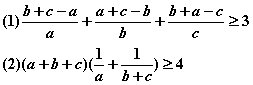
例6 已知f(x)=x2-x+13，且x-a<1，
求证：
三、习题
1．已知a+b+c=0，且acb>0，设
，则（ ）．
（A）M>0 （B）M<0
（C）M=0 （D）M的正负不能确定
2．已知a,bÎR，且a¹b，则（ ）．
（A）
（B）
（C）
（D）
3．设x,y,aÎR，且m>0，那么
且
是
成立的（ ）．
（A）充分非必要条件 （B）必要非充分条件
（C）充分必要条件 （D）既非充分条件也非必要条件
4．若ab>0，则下列不等关系中不能成立的是（ ）．
（A）
（B）
（C） 
（D）
5．设x>0，y>0，且x+y£4，那么列不等式中总成立的是（ ）．
（A）
（B）
（C）
（D）