崇文区统练（一）高三数学（理科）

崇文区2005年统练（一）

高三数学（理科）

　  本试卷分第I卷（选择题）和第II卷（非选择题）两部分。共150分。考试时间120分钟。

第I卷（选择题共40分）

参考公式：

三角函数的积化和差公式

　　

　　

3　　　　　 选择题：本大题共8小题；每小题5分，共40分。 在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）函数y = sin（x +）是偶函数，则的一个值是　（　　）

　　（A）　　　　（B）　　　　（C）　　　　（D）2

（2）平面内有一固定线路AB， AB = 4，动点P满足 PA － PB = 3，O为AB中点，则OP的最小值为　（　　）

　　（A）3　　　　　 （B）2　　　　 （C）　　　　（D）1

（3）下列不等式中成立的是　（　　）

　　（A）sin（）＞sin（）　　 （B）cos（）＞cos（）

　　（C）tg（）＞tg（）　　　（D）ctg（）＞ctg（）

（4）直线l₁与l₂互相平行的一个充分条件是　（　　）

　　（A）l₁，l₂都平行于同一平面　　　 （B）l₁，l₂与同一平面所成的角相等

　　（C）l₁平行l₂所在的平面　　　　  （D）l₁，l₂都垂直于同一平面

（5）极坐标方程的图形是　（　　）

　

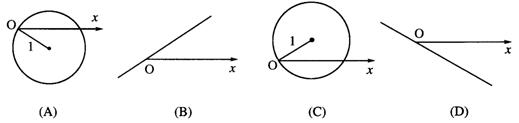
（6）6本不同的图书全部分给2个学生，每个学生最多4本，则不同的分法种数为 （　　）

　　（A）35　　　 （B）50　　　　（C）70　　　　（D）100

（7）无穷等比数列{a_n}的首项a₁ = 3，前n项和为S_n且，则等于 （　　）

　　（A）2　　　　 （B）－2　　　　  （C）6　　　　 　（D）－6

（8）设函数y = f（x）的图象与函数y = 2^x－1的图象关于直线y = x对称，则函数f（x²－x－3）的单调递减区间为　（　　）

　　（A）（）　　　　　　　　  （B）（－∞，]

　　（C）（2，+∞）　　　　　　　　　 （D）[，+∞

第II卷（非选择题共110分）

二、填空题：本大题共6小题，每小题5分，共30分。把答案填在题中横线上。

（9）复数的共轭复数的平方是__________.

（10）已知两点P₁（－1，2）、P₂（2，－3），点P（x，1）分所成的比为=______；x =_______.

（11）已知某海滨浴场的海浪高度y（米）是时间t（0≤t≤24，单位：小时）的函数，记作y = f（t）. 下表是某日各时的浪高数据：

t（时）	0	3	6	9	12	15	18	21	24
y（米）	1.5	1.0	0.5	1.0	1.5	1	0.5	0.99	1.5

　　　经长期观测，y = f（t）的曲线可近似地看成是函数y = Acoswt + b，根据以上数据，函数的解析式为___________________

（12）设全集为R，若集合A = {xx²－3x +2＜0　，集合B = {x logx + log(x + 1)＜－1 ，则是=___________；∪____________.

（13）已知二次函数f（x）= x²－3x + p－1，若在区间[0，1]内至少存在一个实数c，使f（c）＞0，则实数P的取值范围是_____________.

（14）正四棱锥的全面积为2，当正四棱锥的高为h时，底面边长a = _____；体积V的最大值为__________.

三、解答题：本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤。

（15）（本小题满分12分）

在△ABC中，角A、B、C的对边分别为a、b、c，且满足4sin²

（Ⅰ）求角B的度数；

（Ⅱ）如果b =，a + c = 3且a＞c，求a、c的值.

（16）（本小题满分15分）

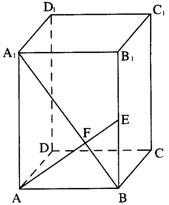
如图，已知正四棱柱ABCD—A₁B₁C₁D₁的底面边长为3，侧棱长为4，连结A₁B，过A作AF⊥A₁B垂足为F，且AF的延长线交B₁B于E。

（Ⅰ）求证：D₁B⊥平面AEC；

（Ⅱ）求三棱锥B—AEC的体积；

（Ⅲ）求二面角B—AE—C的大小.

（17）（本小题满分12分）

某地区预计从2005年初的前n个月内，对某种商品的需求总量f（n）（万件）与月份n的近似关系为f（n）=n（n + 1）（35－2n）（n∈N，n≤12）.

（Ⅰ）求2005年第n个月的需求量g（n）（万件）与月份n的函数关系式，并求出哪个月份的需求量超过1.4万件.

（Ⅱ）如果将该商品每月都投放市场P万件，要保持每月都满足供应，则P至少为多少万件？

（18）（本小题满分13分）

已知等差数列{a_n}的公差不为零，首项a₁ = 2且前n项和为S_n.

（Ⅰ）当S₉ = 36时，在数列{a_n}中找一项a_m（m∈N），使得a₃，a₉，a_m成为等比数列，求m的值.

（Ⅱ）当a₃ = 6时，若自然数n₁，n₂，…，n_k，…满足3＜n₁＜n₂＜…＜n_k＜…并且a₁，a₃，a_n，a_n，…，a_n，…是等比数列，求n_k的值.

（19）（本小题满分13分）

设不等边三角形ABC的外心与重心分别为M、G，若A（－1，0），B（1，0）且MG∥AB .

（Ⅰ）求三角形ABC顶点C的轨迹方程；

（Ⅱ）设顶点C的轨迹为D，已知直线l过点（0，1）并且与曲线D交于P、N两点，若O为坐标原点，满足OP⊥ON，求直线l的方程 .

（20）本小题满分15分

已知函数f（x）=（其中x≥1且x≠2）.

（Ⅰ）求函数f（x）的反函数f；

（Ⅱ）设g(x) =，求函数g（x）最小值及相应的x值；

（Ⅲ）若不等式（1－）·f ＞m（m－）对于区间〔〕上的每一个x值都成立，求实数m的取值范围.

数学（理科）参考答案

一、选择题

（1）B　 （2）C　 （3）D　 （4）D　 （5）C　　（6）B　　（7）A　　（8）A

二、填空题

（9）　　 （10）　　 （11）y =

（12）{x x≤1} ；{x x≤1或x≥2}　　（13）（1，+∞）　 （14）

三、解答题

（15）解（Ⅰ）在△ABC中，A + B + C = 180°，

由4sin²

得4·　　 （3分）

所以，4cos²B－4cosB + 1 = 0，

于是，cosB =, B = 60°.　　　　（6分）

　　（Ⅱ）根据余弦定理有b² = a² + c²－2accosB，

　　　　  又b =，a + c = 3.

　　　　  所以，3 = (a + c)²－2ac－2accosB，

　　　　  得ac = 2.　　　　　 （10分）

　　　　  又解得a = 2，c = 1.　　　　 （12分）

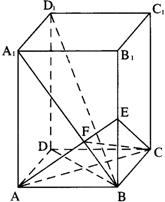
（16）证（Ⅰ）∵ABCD­­­­—A₁B₁C₁D₁是正四棱柱，

∴D₁D⊥ABCD.

连AC，又底面ABCD是正方形，

∴AC⊥BD，

由三垂线定理知　D₁B⊥AC.

同理，D₁B⊥AE，AE∩AC = A，

∴D₁B⊥平面AEC .　　　　  （5分）

　　解（Ⅱ）V_B－AEC = V_E－ABC .

　　　　　  ∵EB⊥平面ABC，

∴EB的长为E点到平面ABC的距离.

∵Rt△ABE ~ Rt△A₁AB，

∴EB =

∴V_B－AEC = V_E－ABC =S_△ABC·EB

　　　　=××3×3×

　　　　=　　　　 （10分）

　　解（Ⅲ）连CF，

　　　　　  ∵CB⊥平面A₁B₁BA，又BF⊥AE，

由三垂线定理知，CF⊥AE .

于是，∠BFC为二面角B—AE—C的平面角，

在Rt△ABE中，BF =，

在Rt△CBF中，tg∠BFC =，

∴∠BFC = arctg.

即二面角B—AE—C的大小为arctg.　　　　（15分）

（17）解（Ⅰ）由题意知，g（1）= f（1）=，

当n≥2时，g（n）= f（n）－f（n－1）

　　　　　　　 =n（n + 1）（35－2n）－（n－1）n〔35－2（n－1）〕

　　　　　　　 =n〔（n + 1）（35－2n）－（n－1）（37－2n）〕

　 　　　　　　=n（12－n）.

又

∴g（n）=(n∈N，n≤12).　　　　（5分）

由n(12－n)＞1.4，得n²－12n + 35＜0，

∴5＜n＜7，又n∈N，∴n = 6，

即6月份的需求量超过1.4万件.　　　　 （7分）

　　　（Ⅱ）要保持每个月都满足供应，则每月投放市场的商品数P（万件）应满足P_n≥f（n）.

　　　　　  即P_n≥n（n + 1）（35－2n）.

　　　　　  ∴P≥（n + 1）（35－2n）=－，

　　　　　  ∵n∈N，当n = 8时，（n + 1）（35－2n）的最大值为1.14万件.

　　　　　  即P至少为1.14万件.　　　　（12分）

（18）解（Ⅰ）∵数列{a_n}的公差d≠0，a₁ = 2，S₉ = 36，

∴36 = 9 × 2 +× 9 × 8d，

∴d =，∴a₃ = 3, a₉ = 6.　　　　  （3分）

由a₃, a₉, a_m成等比数列，

则a，得a_m = 12，

又12 = 2 +（m－1）×，

∴m = 21.　　　 （7分）

　　　　（Ⅱ）∵{a_n}是等差数列，a₁ = 2，a₃ = 6，∴d = 2.

∴a_n = 2n.

又a₁，a₃，成等比数列，∴公比q = 3，

∴= a₁·q^{k + 1}=2·3^{k + 1},

又是等差数列中的项，

∴= 2n_k，∴2n_k = 2·3^{k + 1}，

∴n_k = 3^{k + 1}(k∈N).　　　　 （13分）

（19）解（Ⅰ）设C（x，y）（xy≠0）.

∵MG∥AB，可设G（a、b），则M（0，b）.

∴x = 3a，y = 3b.　　　 ①

∵M是不等边三角形ABC的外心，

∴ MA = MC ，即　　　 ②

由①②得　x² +,

∴三角形顶点C的轨迹方程为x² +(xy≠0).　　  （5分）

　　　　（Ⅱ）设直线l的方程为y = kx + 1，又设P（x₁，y₁），N（x₂，y₂）.

由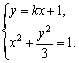消y，得(3 + k²) x² + 2kx－2 = 0，

∵直线l与曲线D交于P、N两点，

∴b²－4ac = 4k² + 8(3 + k²)＞0.

又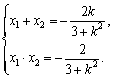

∵OP⊥ON，

∴x₁x₂ + y₁y₂ = 0，

∴x₁x₂ + (kx₁ + 1)(kx₂ + 1) = 0,

∴(1+ k²) x₁x₂ + k(x₁ + x₂) + 1 = 0,

∴(1+ k²) () + k() +1= 0.

∴k =

∴直线l的方程为y =x + 1.　　 （13分）

（20）解（Ⅰ）f（x）=（x≥1且x≠2）.

∵0≤＜1且≠，

∴函数f（x）=的值域为〔0，∪（，1）.

由f（x）=，得，

因此，函数y = f（x）的反函数　　x∈〔0，　∪（，1）.

(6分)

　　　　（Ⅱ）≥2+1，

当且仅当.　　（10分）

　　　　（Ⅲ）由（1－）·＞m（m），

　　　　　　  得1+＞m²－m.

设= t，则( t ) = (1 + m) (t + 1－m).

根据题意，对区间〔〕中的一切t值，( t ) ＞0恒成立.

则　　　　　　 得

∴　　　　　　　　  ∴－1＜m＜.

即实数m的取值范围是m∈（－1，）.　　　　（15分）