江苏省白蒲高级中学2005-2006学年度第二学期阶段考试
高三数学试题（理） （2006.2.25）
时间：120分钟 总分：150分
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1、等差数列
中,若
,则
的值是
A、64 B、31 C、30 D、 15
2、直线
与直线
的夹角是
A、
B、
C、
D、
3、若抛物线
过点
, 则点A与抛物线焦点F的距离为 A、9
B、10
C、12
D、4
4、已知
是
上的单调增函数，则
的取值是
A、
或
B、b≤
1或b≥2 C、
D、1≤b≤2
5、若P：
, Q：
,则P 是Q的
A、充分而不必要条件 B、必要而不充分条件
C、充要条件 D、即不充分也不必要条件
6、集合P{(x, y)y=k}, Q={(x,y)y=ax+1, a>0, a≠1}，已知P∩Q只有一个子集，那么实数k的取值范围是
A、（－∞，1） B、
C、（1，+∞） D、R
7、设
,若
,则n的值为
A、7 B、 11 C、15 D、 16
8、有一棱长为a的正方体框架，其内放置一气球，使其充气且尽可能地膨胀（仍
保持为球的形状），则气球表面积的最大值为
A、
B、2
C、3
D、4
9、用0，1，2，3，4这5个数字组成无重复数字的五位数，其中恰有一个偶数字夹在两个奇数字之间的五位数的个数有
A、48个 B、36个 C、28个 D、12个
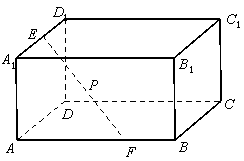
10、在长方体
中，
，点
分别在棱
、
上
滑动，且线段
的长恒等于2，则线段的中点
的轨迹是
A、圆的一部分 B、椭圆的一部分
C、双曲线的一部分 D、抛物线的一部分
 |
11、设O点在
内部，且有
，则的面积与
的面积的比为
A、2 B、
C、3 D、
12、已知双曲线
的左、右焦点分别为F1、F2，点P在双曲线的右支上，若此双曲线的离心率为e，且PF1=ePF2，则e的最大值为
A、
B、
C、2
D、1
第Ⅱ卷(非选择题 共90分)
二、填空题：本大题共6小题,每小题4分,共24分.把答案填写在答题卡相应位置上.
13、已知
，则
=______________
14、设直线
和圆
相交于两点A、B，则弦AB的垂直平分线方程为__________________
15、设
是两条不同的直线，
是两条不同的平面，在下列四个命题：①若
则
；②若
，则
；③若
则
；④若
，则
中正确的命题有__________(只填序号)
16、五个身高均不相同的学生排成一排,则高个子恰好站中间,且从中间到左边和从
中间到右边均一个比一个矮的概率为_________________
17、若函数
的值域为R，则实数a的取值范围是______________________
18、在等比数列中，
，且
，则使
的最大自然数n的值为_________________
三、本大题共5小题，共66分。解答应写出文字说明、证明过程或演算步骤。
19、（本小题满分12分）
某学校从5名男生和名2女生中任意派3人参加市教育局组织的演讲比赛.
(1) 求该学校所派3名选手都是男生的概率；
(2) 求男生、女生都有选手参加比赛的概率；
(3) 如果参加演讲比赛的每位选手获奖的概率均为
, 则该学校恰好有2名选手获奖的概率是多少?
20、（本小题满分12分）
经过抛物线y
的焦点F的直线l与该抛物线交于A,B两点.
(1) 试求线段AB的中点M的轨迹方程；
(2) 若直线l的斜率k＞2，且点M到直线3 x+4y+m=0的距离为
，试确定m的取值范围。
21、（本小题满分14分）
如图，梯形
中，
，
=
，
是的中点，将
沿
折起，使点
折到点的位置，且二面角
的大小为
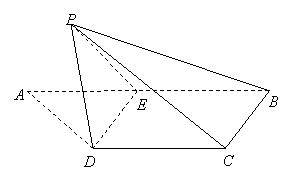（1）求证：
；
（2）求直线
与平面
所成角的大小；
（3）求点
到平面
的距离。
22、（本题满分14分）
已知
是函数
的一个极值点，其中
，且
。
（Ⅰ）求
与
的关系表达式；
（Ⅱ）求
的单调区间；
（Ⅲ）当
，
时，函数
的图像上任意一点的切线斜率恒大于
，求的取值范围。
23、（本小题满分14分）
已知函数
。
（Ⅰ）用a表示f(2)、f(3)并化简；
（Ⅱ）比较f(2)－2与f(1)－1，f(3)－3 与f(2)－2的大小关系，并由此归纳出一个更一般的结论（此结论不要求写出证明过程）；
（Ⅲ）比较
与
，
与的大小关系，并由此归纳出一个更一般的结论，并加以证明。
答案：
一、D，A，B，D，A，B，B，B，C，A，C，D
二、13、
14、x+y=1
15、（4）
16、
17、
18、8
三、19、
20、(1)设A(
直线AB的方程为y=k(x-1) (k≠0),代入
,得 k
x-(2k+4)x+k=0
设M(x ,y).则
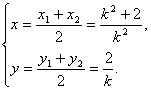
∴点M的坐标为(
消去k可得M的轨迹方程为
(2)由 d=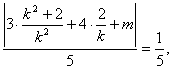
得
即
0＜
＜
,得
0＜
,
即 
或 
故的取值范围为 (-
21、（1）略
（2）
（3）
22、
（2）、（3）略
23、（Ⅰ）
…………2分
（Ⅱ）
,一般地,f(n+1) －(n+1)> f(n) －n(n∈N*) …………………………………………5分
(
所以
……………………………6分
判断
,证明如下:
(*)
因为
,
,所以(*)式显然成立,所以.…8分
一般地
(n∈N*)
…………………………………………9分
证明如下: 
>0
,此式显然成立,故(n∈N*)…………………14分