第一学期高三期末统一练习数学（文史类）

崇文区2005—2006学年度第一学期高三期末统一练习

数学（文史类）

本试卷分第一卷（选择题）和第二卷（非选择题）两部分。第一卷１—2页，第二卷3—9页。满分120分，考试时间120分钟。考试结束，将本试卷和答题卡一并交回。

第一卷（选择题，共40分）

注意事项：

1．　答第一卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．　每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试卷上。

一、本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项.

1．　设全集U=R,A={xx＜2} ,B={xx-1≤3},则（C_UA）∩B=

A．[-2，4]　　　　　　 B.(-∞,-2]　　　　  C.[2,4]　　　　 D.[2,+∞)

2.圆x²+y²=4与直线l:x=a相切，则a等于

A．2　　　　　　　　　  B.2或-2　　　　　  C.-2　　　　　  D.4

3．下列命题中，正确的是

A．　如果一个平面内的两条直线与另一个平面平行，则这两个平面平行

B．　如果一个平面内的无数条直线与另一个平面平行，则这两个平面平行

C．　如果一个平面内的两条直线分别与另一个平面内的两条直线平行，则这两个平面平行

D．　如果一个平面内的两条相交直线分别与另一个平面内的两条直线平行，则这两个平面平行

4．　函数y=cosx，x∈[-的值域是

A．[0，1]　　　　　 B.[-1,1]　　　　　　 C.[0,　　  D.[-

5.△ABC中，若则△ABC为

 A．锐角三角形　　　　 B.钝角三角形　　　　C.直角三角形　　  D.以上均有可能

6. 是的

 A．充分必要条件　　　　　　　　　　　　　　 B. 充分而不必要条件

 C．必要而不充分条件　　　　　　　　　　　　 D.既不充分也不必要条件

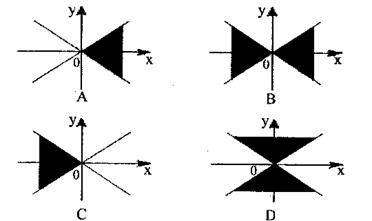7．在直角坐标系内，满足不等式x²-y²≤0的点（x,y）的集合（用阴影表示）是

8．要得到函数y=3cos(2x-的图象，可以将函数y=3sin(2x-的图象沿x轴

　A．向左平移个单位　　　　　　　　　　  B.向右平移个单位

　C．向左平移个单位　　　　　　　　　  　D.向右平移个单位

第二卷（共110分）

注意事项：t x

1．　用钢笔或圆珠笔将答案填写在试卷上.

2．　答卷前将密封线内的项目填写清楚.

二、填空题：本大题共6小题，每小题5分，共30分.把答案填在题中横线上.

9．二次式(1-的项的系数是_____________.（作数字作答）

10.已知函数f(x)=log₃(，它的反函数为y=f^-1(x)，则f^-1(1)=__________，y=f^-1(x)的定义域为______________.

11.若数列{a_n}的前n项和为S_n，且满足S_n=a_n+1(n≥1)，则a_n=___________.

12.若定义运算a*b=则函数f(x)=3^**3^x的值域是______________.

13.某区全运动会共有28个参赛队，开幕式入场顺序按参赛队队名（英文字母）第一个字母从A到Z顺序排列.若不同的队第一个字母相同，则他们之间随机排列.报名统计时发现26个字母中的每一个都有参赛队与之对应，则开幕式的入场排列方式最多有________种，最少有_________种.

14.下列命题：

①　　 若不等式x-4＜a的解集非空，则必有a＞0;

②　　 函数cosa=0,则sina=1;

③　　 函数y=f(1+x)与函数y=f(1-x)的图象关于直线x=1对称；

④　　 若f(x+a)=f(a-x)，则函数y=f(x)的图象关于直线x=a对称.

其中错误的命题的序号是_____________（把你认为错误的命题的序号都填上）.

三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.

15.（本题满分13分）

　 已知二次函数f(x)=x²-2x-3的图象为曲线C，点P（0,-3）.

（1）　　　 求过点P且与曲线C相切的直线的斜率；

（2）　　　 求函数g(x)=f（x）的单调递增区间.

16. （本题满分13分）

已知盒子内有3个正品元件和4个次品元件，乙盒了内有5个正品元件和4个次品元件，试求：

（1）　　　 从甲盒子内取出2个元件，恰有一件正品元件一件次品的概率；

（2）　　　 从两个盒子内各取出2个元件，取得4个元件均为正品的概率；

（3）　　　 从两个盒子各取出2个元件，取得的4个元件中至少有3个元件为正品的概率.

17．（本题满分14分）

　 在四棱锥P-ABCD中，AB⊥CD，CD∥AB，PD⊥底面ABCD，AB=AD，直线PA与底面ABCD成60°，M、N分别是PA、PB的中点.

（1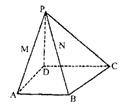）　　　 求证：直线MN∥平面PDC；

（2）　　　 求平面MNCD与平面ABCD所成二面角的大小；

（3）　　　 若∠CND=90°，求证：直线DN⊥平面PBC；

18．（本题满分12分）

已知y_n=2log_ax_n（a＞0且a≠1，n∈N^*）,已知y₄=17,y₇=11.

（1）　　　 求证：数列{y_n}是等比数列；

（2）　　　 数列{y_n}的通项公式；

（3）　　　 数列{y_n}的前多少项的和为最大？最大值为多少？

19. （本题满分14分）

已知中心在原点的双曲线C的右焦点为（2，0），实轴长为2.

（1）　　　 求双曲线C的方程；

（2）　　　 若直线l:y=kx+与双曲线C恒有两个不同的交点A和B，求k的取值范围；

（3）　　　 在（2）的条件下，若（其中O为原点），求k的取值范围.

20.(本题满分14分)

　　对于函数y=f(x)，若同时满足下列条件：

①　　 函数y=f(x)在定义域D内是单调递增或单调递减函数；

②　　 存在区间[a,b]D，使函数f(x)在[a,b]上的值域为[a,b]，则称f(x)是D上的闭函数.

（1）　　　 求闭函数f(x)=-x³符合条件②的区间[a,b]；

（2）　　　 判断函数g(x)=在区间(0,+∞)上是否为闭函数；

（3）　　　 若函数φ(x)=k+是闭函数，求实数k的取值范围.

崇文区2005—2006学年度第一学期高三期末统一练习

1.C　2.D  3.D　4.C 5.C　6.B 7.D 8.A

9.70　10.I,R　11. 　12.(0,1]　 12.　13.6,4　14. (2)(3)

15.(1)∵f(x)=x²-2x-3,∴f′(x)=2x-2.

　　　∵点P坐标是（0，-3），∴点P在曲线C上. ∴f′(0)=-2.

∴过点P且与曲线C相切的直线的斜率是-2.

（2）∵g(x)=f(x)=x²-2x-3=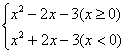

∴g′(x)=

∴由图象可知，函数g(x)的单调递增区间为[-1,0],[1,+∞].

16.(1)设A=“从甲盒子内取出2个元件，恰有一件正品，一件次品”，

　　　则P（A）=

　 （2）设B=“从两个盒子内各取2个元件，取得的4个元件均为正品”，

　　 则P（B）=.

　 (3)设C=“从两个盒子内各取2个元件，取得的4个元件至少有3个元件为正品”,

　则P（C）=

17．（1）证明：∵M、N是PA、PB中点，

　　　　　　  ∴MN∥AB，从而MN∥CD.

∵MN在平面PDC外，CD在平面PDC内，

∴直线MN∥平面PDC.

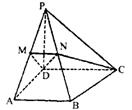  (2) ∵PD⊥底面ABCD，DC底面ABCD，

　　　∴PD⊥CD.

　　又CD∥AB，AB⊥AD，

　　∴CD⊥AD.

　　∴CD⊥面PAD.

　　∴CD⊥MD.

　　∴∠MAD为平面MNCD与平面ABCD所成二面角的平面角.

　　∴PD⊥底面ABCD.

　　∵M是PA的中点，

∴MD=MA.

∴∠MDA=60°.

∴平面MNCD与平面ABCD所成二面角的平面角为60°.

　（3）证明：∵AB⊥AD，AB=AD，

　　　　　　 ∴BD=AD.

　　　　　　 ∵PD⊥底面ABCD，直线PA与底面ABCD成60°角，

　　　　　　 ∴PD=AD.

　　　　　　 ∴PD=BD.

　　　　　　 ∵N是PB的中点，

　　　　　　 ∴DN⊥PB.

　　　　　　 ∵∠CND=90°，

　　　　　　 ∴DN⊥CD.

　　　　　　 ∵PB、CN相交于一点N，

　　　　　　 ∴直线DN⊥平面PBC.

18．(1)证明：∵y_n+1-y_n=2log_a()ⁿ⁺¹-2log_a()ⁿ=2log_a()常数(n≥1).

　　　　∴数列{y_n}为等差数列.

　　(2)设数列{y_n}的公差为d,由y₄=17,y₇=11.

　　　 得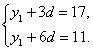

　　解得y₁=23,d=-2,

　　　∴y_n=25-2n.

　　 即数列{yn}的通项为y_n=25-2n(n≥1).

 (3)解：令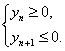

得

 ∵n∈N^*.

　∴n=12.

　∴{y_n}的前12项之和最大，最大值为S₁₂=144.

(3)由（2）知，当n＞12时,y_n＜0成立.

　∵y_n=2log_ax_n，

　∴x_n=a.

　当a＞1，且n＞12时，有x_n=a＜a=1.

　这与题意不符，故0＜a＜1.

　由0＜a＜1,且n＞12，有x_n=a≥a＞2.

　故所求a的取值范围为0＜a＜

19．（1）设双曲线方程为(a＞0,b＞0),

　　　　由已知得a=,c=2,

　　　 再由a²+b²=c², ∴b²=1.

　　　∴双曲线方程为

　(2)将y=kx+代入.

　得(1-3k²)x²-6kx-9=0.

　由题意知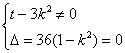即k²≠，且k²=1.　 ①

　 ∴k的取值范围为（-1, ∪(-∪(

（3）设A（x_A,y_A），B（x_B,y_B）.

　　 由（2）得x_A+x_B=x_A·x_B=

　　 由得x_A·x_B+y_A·y_B＞2,

　 　而x_A·x_B+y_A·y_B=x_A·x_B+(kx_A+(kx_B+

　　 =(k²+1)x_A·x_B+k(x_A+x_B)+2

　　 =(k²+1)·

　　于是

　 ∴　　　　  ②

　　由①②得

　　故k的取值范围为(-1,-

20.(1) ∵y=-x³是[a,b]上的减函数，

　　　　∴

∴

∴(

∴

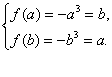
又∵-a³=b,

 ∴

∴所求区间为[-1,1].

　(2)∵g′(x)=∈(0,+∞),

令g′(x)= ＞0,得x＞

∴x＞时，g(x)为（，＋∞）上的增函数。

令g′(x)＝<0，得0<x<

　　∴g(x)为（0，）上的减函数.

　　∴g(x)不是（0,+∞）上的单调函数.

　　∴g(x)不是（0，+∞）上的闭函数.

（3）易知φ(x)是[-2,+∞]上的增函数.

　　 设φ（x）=k+满足条件②的区间是[a,b]，

　　 ∴

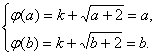
　即a,b是方程x=k+的两个不等实根.

　也就是方程组　有两个不等实根a,b.

①　　 当k≤-2时，方程x²-(2k+1)+(k²-2)=0在[-2,+∞）上有两个不等实根.

∴

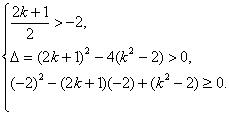
　解得：-

②　　 当k＞-2时，方程x²-(2k+1)x+(k²-2)=0在[k,+∞）上有两个不等实根.

∴

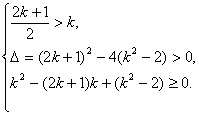
解得：-与条件k＞-2矛盾.

∴φ(x)=k+是闭函数，实数k的取值范围是-