浙江省杭州学军中学2007学年度高三年级第一次月考
数学试卷（理）
YCY
第Ⅰ卷（选择题 共50分）
一、选择题：本大题共10小题，每小题5分，共50分.
1．设随机变量ξ的分布列由
的值为 （ ）
A．1 B．
C．
D．
2．
的展开式中，不含x的项为
，则正数p的值为 （ ）
A．1 B．2 C．3 D．4
3．四棱锥P—ABCD的所有棱长都是a，E为PC中点，则直线PA到面BDE的距离为（ ）
A．
B．
C．
D．
4．已知二面角
的平面角是60°，若
内有一点A到
，则A在β上的射影A′到的距离为 （ ）
A．1 B．
C．
D．2
5．已知随机变量ξ服从二项分布ξ~
（ ）
A．6 B．4 C．3 D．9
6．有7只发光的二极管排成一排，每只二极管点亮时可发红光或绿光，若每次恰有3只二极管点亮，但相邻的两只二极管不能同时点亮，根据这三只点亮的二极管的不同位置或不同颜色来表示不同信息，则这排二极管能表示的信息种数共有 （ ）
A．10 B．48 C．60 D．80
7．函数f (x) = x 在x = 0处 （ ）
A．不存在极限 B．连续且可导 C．连续且不可导 D．在（0,0）处有切线
8．
（ ）
A．
B．1 C．2 D．不存在
9．已知f (x) = (x－1)(x－2)…(x－2006)，则f ′(2006)等于 （ ）
A．0 B．2006 C．2005！ D．2006！
10．如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是 （ ）
A．等腰四棱锥的腰与底面所成的角都相等
B．等腰四棱锥的侧面与底面所成的二面角都相等或互补
C．等腰四棱锥的底面四边形必存在外接圆
D．等腰四棱锥的各顶点必在同一球面上
|
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中的横线上.
11．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2 ：3 ：4，现用分层抽样方法抽出一个容量为n的样本，样本中A种型号的产品有16件，则n = ；
12．已知过球面上三点A、B、C的截面到球心的距离等于球的半径的一半，且AC=BC=6，AB = 4，则球的表面积为 ；
13．设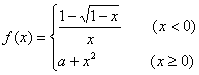
，要使f (x)在x =
0处连续，则实数a的值为 ；
14．四面体ABCD中，（1）若AC⊥BD，AB⊥CD，则AD⊥BC；（2）若E、F、G分别是BC、AB、CD中点，则∠FEG的大小等于直线AC、BD所成角大小；（3）若O为四面全ABCD外接球球心，则O在面ABD上的射影是△ABD的外心；（4）若四个面是全等三角形，则ABCD是正四面体。其中正确的命题是 。
三、解答题：本大题共6小题，每题14分，共84分.解答应写出必要的文字说明、证明过程及演算步骤.
15．已知函数
处取得极值，并且它的图象与直线
y =－3x + 3在点（1，0）处相切，求a、b、c的值.
16．求函数
在[0，2]上的最大值与最小值.
17．某射手进行射击训练，假设每次射击击中目标的概率为
，且各次射击的结果互不影响.
（1）求射手在3次射击中，至少有两次连续击中目标的概率；
（2）求射手第3次击中目标时，恰好射击了4次的概率；
（3）设随机变量
表示射手第3次击中目标时已射击的次数，求的分布列.
18．（1）求值：
；
（2）令
，画出函数f (x)的图象并判断
是否存在，说明理由.
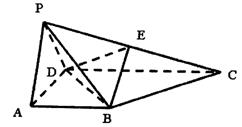
19．已知在四棱锥P—ABCD中，底面ABCD是直角梯形，∠BAD = 90°，2AB=2AD=CD，侧面PAD是正三角形且垂直于底面ABCD，E是PC上一点.
（1）点E是PC中点时，求证：BE⊥平面PCD；
（2）在（1）的条件下，求二面角C—BD—E的大小；
|
20．已知点的序列
，A3是线段A1A2的中点，A4的线段A2A3的中点，…，An是线段An－2An－1的中点，…
（1）写出
、
之间的关系式（n≥3）；
（2）设
，计算
由此推测数列
的通项公式，并用数学归纳法加以证明.
参考答案
一、选择题：本大题共10小题，每小题5分，共50分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | A | B | A | D | C | A | C | B |
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中的横线上.
11．72； 12．54π 13．
14．（1）（3）
三、解答题：本大题共6小题，每题14分，共84分.解答应写出必要的文字说明、证明过程及演算步骤.
15．
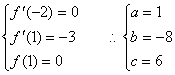
16．
| x | 0 | （0，1） | 1 | （1，2） | 2 |
| y′ | + | － | |||
| y | 0 | Ln2－ | Ln3－1 |
∴当x =
0时，
；当x = 1时；
17．（1）
（2）
|
| 3 | 4 | 5 | … | n | … |
| P |
|
|
|
|
18．（1）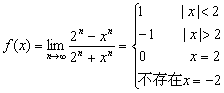
（2）不存在，（图略）
|
CD⊥平面PAD，∴AG⊥CD，
∴AG⊥平面PCD.
又∵EG∥CD∥AB，且EG
= 
，
∴BE∥AG，从而BE⊥平面PCD.
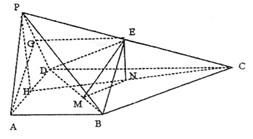
（2）解：取AD中点H，连结PH、HC，
取HC中点N，过N作MN⊥BD于点M，连ME.
由条件易得：PH⊥平面ABCD，又N、E分别是HC和PC的中点，∴EN⊥平面ABCD，则由三垂线定理得：EM⊥BD，故∠EMN就是所求二面角的平面角.设AB = AD = a，则
，
，
∴在Rt△EMN中，
|
，∴所求二面角的大小为
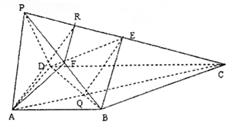
（3）存在PB中点F，使AF∥平面BDE.
证明：连结AC交BD于点Q，取PE中点R，连结FR，
∵AQ ：QC = AB ：CD = 1 ：2，RE ：EC = 1 ：2，
∴AR∥QE， ∴AR∥平面BDE， 又RF∥BE，
∴RF∥平面BDE ∴平面AEF∥平面BDE
20．（1）
（2）
