省镇中高三数学月考试卷2006.03
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1、
设集合![]() ,则
,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、
函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3、
如果![]() 且
且![]() ,则
,则![]() 可以是 ( )
可以是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、![]() 是两个不重合的平面,在下列条件中,可判定平面
是两个不重合的平面,在下列条件中,可判定平面![]() 与
与![]() 平行的是
( )
平行的是
( )
A.m,n是![]() 内的两条直线,且
内的两条直线,且![]()
B.![]() 都垂直于平面
都垂直于平面![]()
C.![]() 内不共线三点到
内不共线三点到![]() 的距离相等
的距离相等
D.m,n是两条异面直线,![]()
5、已知数列![]() 的前
的前![]() 项和
项和![]() ( )
( )
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列、或者是等比数列 D.等差、等比数列都不是
6、已知实数![]() 满足
满足![]() .
.
命题P:函数![]() 在区间[0,1]上是减函数.
在区间[0,1]上是减函数.
命题Q:![]() 是
是![]() 的充分不必要条件.则( )
的充分不必要条件.则( )
A.“P或Q”为真命题; B.“P且Q”为假命题;
C.“┐P且Q”为真命题; D.“┐P或┐Q”为真命题
7、教师想从52个学生中抽取10名分析期中考试情况,一小孩在旁边随手拿了两个签,教师没在意,在余下的50个签中抽了10名学生.则其中的李明被小孩拿去和被教师抽到的概率分别为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
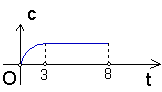 8、某工厂8年来某种产品的总产量c与时间t(年)的函数关系如右图,下列四种说法:①前三年中产品增长的速度越来越快;②前三年中产品增长的速度越来越慢;③第三年后,这种产品停止生产;④第三年后,年产量保持不变,其中正确的说法是 (
) ( )
8、某工厂8年来某种产品的总产量c与时间t(年)的函数关系如右图,下列四种说法:①前三年中产品增长的速度越来越快;②前三年中产品增长的速度越来越慢;③第三年后,这种产品停止生产;④第三年后,年产量保持不变,其中正确的说法是 (
) ( )
A.②和③ B.①和④
C.①和③ D.②和④
9、若双曲线的焦点到渐近线的距离等于实轴长,则该双曲线的离心率![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、某商场宣传在“五一黄金周”期间对顾客购物实行一定的优惠,商场规定:
①如一次性购物不超过200元,不予以折扣;
②如一次性购物超过200元但不超过500元的,按标价给予九折优惠;
③如一次性购物超过500元的,其中500元给予9折优惠,超过500元的部分给予八五折优惠.
某人两次去购物,分别付款176元和432元,如果他只去一次购买同样的商品,则应付款( )
A.608元 B.574.1元 C.582.6元 D.456.8元
二、填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上.
11、将正方形ABCD沿对角线BD折成直二面角,有如下结论:①AC⊥BD;
②⊿ABC是等边三角形; ③AB与面BCD成60°角;
④AB与CD成60°角。请你把正确的结论的序号都填上_______________
12、函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 的表达式为
的表达式为
13、若椭圆![]() 上一点
上一点![]() 到右焦点
到右焦点![]() 的距离为
的距离为![]() ,则点P到
,则点P到![]() 轴的距离为
轴的距离为
14、已知向量![]() 满足
满足![]() ,则
,则![]()
15、数列![]() 是等差数列
是等差数列![]() ,则n的值为
,则n的值为
16、若函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() =
=
三、解答题:本大题共5小题,共70分。解答应写出文字说明、证明过程或演算步骤.
17、(本小题满分14分)
已知函数![]() 最小正周期
最小正周期![]() .
.
(1) 求实数![]() 的值;
的值;
(2) 若x是![]() 的最小内角, 求函数
的最小内角, 求函数![]() 的值域
的值域
18、(本小题满分14分)
一根水平放置的长方体形枕木的安全负荷与它的宽度![]() 成正比,与它的厚度
成正比,与它的厚度
![]() 的平方成正比,与它的长度
的平方成正比,与它的长度![]() 的平方成反比.
的平方成反比.
(1)将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷变大吗?为什么?
(2)现有一根横断面为半圆(半圆的半径为![]() )的木材,用它来截取成长方形的枕木,
)的木材,用它来截取成长方形的枕木,
其长度即为枕木规定的长度,问如何截取,可使安全负荷最大?
 |
19、(本小题满分14分)
三棱柱ABC—A1B1C1的底面是边长为4的正三角形,侧面AA1C1C是菱形,
PA⊥BC,点P是A1C1的中点,∠C1CA=60°.
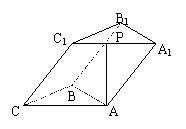 (1)求证:PA⊥平面ABC;
(1)求证:PA⊥平面ABC;
(2)求直线CC1与直线B1P所成角的正弦值;
(3)求四棱锥P—AA1B1B的体积.
20、(本小题满分14分)
在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 、
、![]() 两边所在的直线分别与
两边所在的直线分别与![]() 轴交于原点同侧的点
轴交于原点同侧的点![]() 、
、![]() ,且满足
,且满足![]() (
(![]() 为不等于零的常数).
为不等于零的常数).
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)如果存在直线![]()
![]() ,使
,使![]() 与点
与点![]() 的轨迹相交于不同的
的轨迹相交于不同的![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
21、(本小题满分14分)
已知函数![]() 的反函数为
的反函数为![]()
(1)已知数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 满足
满足![]() ,求证:对一切
,求证:对一切![]() 的正整数,都满足:
的正整数,都满足:![]() .
.
参考答案
一、选择题
DADDC ABACC
二、填空题
11、①②④ 12、![]() 13、
13、![]() 14、
14、![]() 15、 15 16、6
15、 15 16、6
三、解答题
17.解(1) 因为![]()
所以![]()
![]() .
.
(2)
因为x是![]() 的最小内角, 所以
的最小内角, 所以![]()
又![]() , 所以
, 所以![]()
18.解:.(1)解:安全负荷![]() 为正常数) 翻转
为正常数) 翻转![]()
![]() ,安全负荷变大.当
,安全负荷变大.当
![]() ,安全负荷变小.
,安全负荷变小.
(2)如图,设截取的宽为a,高为d,则![]() .安全负荷
.安全负荷![]() 为正常数)∵枕木长度不变,∴
为正常数)∵枕木长度不变,∴![]() 最大时,安全负荷最大.
最大时,安全负荷最大.

![]()
令![]()
![]() 时
时![]() ,
,
取![]() 时,u最大, 即安全负荷最大.
时,u最大, 即安全负荷最大.
19. 证明:(1)∵四边形AA1C1C是菱形,∠C1CA=60°,∴△AC1A1是正三角形,又P是A1C1
的中点,∴PA⊥A1C1,∴PA⊥AC. 又PA⊥BC,AC∩BC=C ∴PA⊥平面ABC.
(2)由(1),PA⊥平面ABC,∴PA⊥平面 A1B1C1,由△AC1A1是正三角形,∴PB1⊥A1C1,
∴B1P⊥平面AA1C1C,∴B1P⊥CC1. ∴CC1与B1P所成的角的正弦值为1.
(3)![]()
![]()
20.解:(1)设点![]() ,
,![]() .
.
当![]() 时,
时,![]() 轴,当
轴,当![]() 时,
时, ![]() 轴,与题意不符,所以
轴,与题意不符,所以![]() ;
;
由![]() .
.![]() .
.![]() 三点共线有
三点共线有![]() ,解得
,解得![]() .
.
同理由![]() .
.![]() .
.![]() 三点共线,解得
三点共线,解得![]() .
.
![]() ,
, ![]() ,
,
化简得点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)设![]() 的中点为
的中点为![]() ,
,
![]()
![]() ,
,
由![]() ,
,![]() …①
…①
![]() ,
,![]() .
.
![]() ,即
,即![]() ,
, 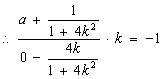
,![]() ,即
,即![]() ………②
………②
![]()
![]() ,
, ![]()
![]() .把②代入①并化简得
.把②代入①并化简得![]()
![]() .
.
当![]() 时,直线
时,直线![]() 过点B,而曲线C不过点B,所以直线
过点B,而曲线C不过点B,所以直线![]() 与曲线C只有一个公共点.故
与曲线C只有一个公共点.故![]() 舍去;故
舍去;故![]() 的取值范围是
的取值范围是![]() 且
且![]() .
.
21.解:![]() 的反函数
的反函数![]()
![]() ,则
,则![]() ,
,![]()
![]() 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列 ![]() ,
, ![]() 则
则![]()
则![]() 时
时![]()
且