2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题F
学校 姓名 营员证号
一．设
，求证：
二．在
中，
分别以
为边，向外作两个三角形：
和
使得 
设
与
交于点
，
与
交于点
，求证：
的充要条件是：
三．对任意两个正整数
与
，有唯一的正整数
与之对应，且函数
具有性质：
对任意正整数
与
，
；
对任意正整数
，
；
对任意正整数
与，当
时，
求证：恰有一个函数满足上述三个性质，并求出这个函数.
四. 设
为任意无穷正实数数列，求证：不等式
对无穷多个正整数
成立.
2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题F解答
学校 姓名 营员证号
一．设，求证：
证：因为
同理 
所以
二．在中，分别以为边，向外作两个三角形：和使得 设与交于点，与交于点，求证：的充要条件是：
证：
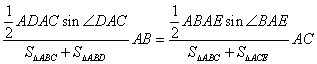
①
由题设条件知
∽
，故
即AD·AC
且
从而①等价于
②
记
由于∽，所以
从而②等价于
因为
，所以
，从而
即
三．对任意两个正整数与，有唯一的正整数与之对应，且函数具有性质：
对任意正整数与，；
对任意正整数，；
对任意正整数与，当时，
求证：恰有一个函数满足上述三个性质，并求出这个函数.
解：取
为
的最小公倍数
显然=满足性质（1），（2）。下证它也满足（3）
若
设
则a与b互质，
故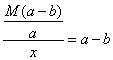
，
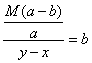
由
知
故
从而
即函数=也满足（3）
下证唯一性。用反证法：若有两个函数
同时满足命题给出的三个性质，
则存在正整数，使得
，设其中s,t是使
，
且
取最小值的一对正整数，
由性质（2），
,故
。由性质（1）不妨设
由性质（3）
故
.但
与
之最小性选择矛盾。
四. 设为任意无穷正实数数列，求证：不等式 对无穷多个正整数成立.
证：用反证法.假设不等式
只对有限多个正整数成立。设这些正整数中最大的一个为
，则对任意的正整数
，上述不等式均不成立，既有
也既
①
由贝努利不等式，有
（正整数
） ②
结合①，②可得, 
③
下面用数学归纳法证明：
其中n是非负整数
④
当
时,④式左边为
，右边也为,故④式成立.
设当
时，④式成立，既有
⑤
在③中取
，并利用⑤，可得
故④式在
时也成立。故④式得证。
由于
，所以 
即
固而存在正整数
，满足
⑥
在④式中取
，得
⑦
结合⑥，⑦知
，这与
矛盾，
故命题得证。