2005年中国东南地区数学奥林匹克冬令营赛前培训
测 试 题 B
学校: 姓名: 营员证号:________
一.
以⊿ABC的三条边作为斜边,分别向形内方向作等腰直角三角形 ![]() 若三点
若三点![]() 在一直线上,
在一直线上,
试求 ![]() 的值.
的值.
二.
平面上给出![]() 个点
个点![]() ,以这些点为端点的集合为M,线段长度的集合为D,
,以这些点为端点的集合为M,线段长度的集合为D,![]() M中长为
M中长为![]() 的线段条数记为
的线段条数记为![]()
证明:![]() 对于D中的最小数
对于D中的最小数![]() 有
有![]()
![]() .
.![]() <
< ![]()
三.
设![]()
![]() 记
记![]() .
.
证明:对每个给定的正整数![]() 数列
数列![]() 中必有一个K次方整数.
中必有一个K次方整数.
四.某人掷硬币,得正面记![]() 分,得背面记
分,得背面记![]() 分,
分,![]() 为互质正整数,
为互质正整数,![]() ),并将每次的得分进行累记,他发现,不论采取怎样的投掷方案以及投掷多少次,恰有
),并将每次的得分进行累记,他发现,不论采取怎样的投掷方案以及投掷多少次,恰有![]() 个分值总是记录不到,例如
个分值总是记录不到,例如![]() 就是其中之一,试确定
就是其中之一,试确定![]() 的值。
的值。
2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题B 解答
学校: 姓名: 营员证号:________
四.
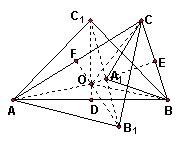 如图,以⊿ABC的三条边作为斜边,分别向形内方向作等腰直角三角形
如图,以⊿ABC的三条边作为斜边,分别向形内方向作等腰直角三角形 ![]() 若三点
若三点![]() 在一直线上,试求
在一直线上,试求 ![]() 的值.
的值.
解:设![]() 的外心为
的外心为![]() ,外接圆半径为单位长,
,外接圆半径为单位长,
作![]() 于
于![]() ,则外心
,则外心![]() 在
在![]() 的中垂线
的中垂线![]() 上,
上,
且圆周角![]() , 于是,
, 于是,
![]() 同理有
同理有 ![]() ,而
,而![]() ,由于
,由于![]() ,则
,则 ![]()
![]() ,
,![]() ,因此,
,因此,
![]()
![]() 同理有,
同理有,
![]()
![]()
![]()
![]()
因为点![]() 共线,则
共线,则 ![]() ,即有
,即有
![]()
![]()
![]() ……1
……1
同除以 ![]() ,得
,得
![]()
![]() ,
,
即 ![]()
![]()
![]() ……2 而在
……2 而在![]() 中, 由于
中, 由于
![]()
因此由2得
![]() .
.
五.
平面上给出![]() 个点
个点![]() ,以这些点为端点的集合为M,线段长度的集合为D,
,以这些点为端点的集合为M,线段长度的集合为D,![]() M中长为
M中长为![]() 的线段条数记为
的线段条数记为![]()
证明:![]() 对于D中的最小数
对于D中的最小数![]() 有
有![]()
![]() .
.![]() <
< ![]()
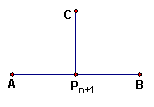 证:
证:![]() 对
对![]() 归纳,当
归纳,当![]() 时显然有
时显然有![]() ,今设命题对于
,今设命题对于![]() 个点成立,考虑
个点成立,考虑![]() 个点的情况,设其中一点
个点的情况,设其中一点![]() 是其凸包的顶点,则
是其凸包的顶点,则![]() 至多引出
至多引出![]() 条长度为最小值
条长度为最小值![]() 的线段.去掉
的线段.去掉![]() 后由归纳假设,剩下
后由归纳假设,剩下![]() 个点,连线中至多有
个点,连线中至多有![]() 条长为最小值
条长为最小值![]() 的线段因此,这
的线段因此,这![]() 个点所成的线段中,成立
个点所成的线段中,成立 ![]() ,从而命题对一切不小于
,从而命题对一切不小于![]() 的
的![]() 皆成立.
皆成立.
![]() 称已知点为“红点”,对于每个红点
称已知点为“红点”,对于每个红点![]() ,若它发出的线段中,有长为
,若它发出的线段中,有长为![]() 的线段
的线段![]() 条,则
条,则![]() ,而以
,而以![]() 为圆心,
为圆心,![]() 为半径所作的圆
为半径所作的圆![]() 上有
上有![]() 个红点,共作成
个红点,共作成![]() 条弦,今过每个这种点都作这种等圆以及相应的弦,共得
条弦,今过每个这种点都作这种等圆以及相应的弦,共得![]() 条弦,每两个圆至多一条公共弦,即这些弦至多重复
条弦,每两个圆至多一条公共弦,即这些弦至多重复![]() 条,因此得到
条,因此得到![]() 条不同的弦,另一方面,
条不同的弦,另一方面,![]() 个红点间两两连线,共计
个红点间两两连线,共计![]() 条,因此,
条,因此,![]() ,由此,
,由此,
![]()

![]()
![]()
即![]() ,
,![]() 因此
因此
![]()
六.
设![]()
![]() 记
记![]() .
.
证明:对每个给定的正整数![]() 数列
数列![]() 中必有一个K次方整数.
中必有一个K次方整数.
证:由于![]() ,故存在
,故存在![]() ,使
,使![]() ,因此有
,因此有![]() ,使
,使
![]() 再设
再设 ![]() ,于是
,于是
![]() 1
1
又因 ![]() ,所以
,所以
![]() 2
2
称1式中的![]() 为数
为数![]() 的“余量”,由于
的“余量”,由于![]() ,则
,则 ![]()
![]() 当
当![]() 时,
时,![]() ,这时
,这时
![]() ,记
,记![]() ,
,
则 ![]()
![]()
所以,![]() 要么是一个
要么是一个![]() 次方数(当
次方数(当![]() ),要么是一个其“余量”比
),要么是一个其“余量”比![]() 的“余量”小
的“余量”小![]() 的数(当
的数(当![]() ),继续此过程,可知,经有限项后,必有某项
),继续此过程,可知,经有限项后,必有某项![]() 是一个
是一个![]() 次方数.
次方数.
![]() 当
当 ![]() 时,
时,![]() 则
则
![]() ,记
,记![]() ,则
,则![]()
![]()
若![]() 则
则 ![]() 为一个
为一个![]() 次方数;
次方数;
若![]() 则
则 ![]() 是一个其“余量”比
是一个其“余量”比![]() 的“余量”少
的“余量”少![]() 的数;
的数;
若![]() 则
则 ![]()
它们都归结为情形![]()
![]() 当
当 ![]() 时,
时,![]() 归结为情形
归结为情形![]()
综合以上讨论,知本题结论成立.
四.某人掷硬币,得正面记![]() 分,得背面记
分,得背面记![]() 分,
分,![]() 为互质正整数,
为互质正整数,![]() ),并将每次的得分进行累记,他发现,不论采取怎样的投掷方案以及投掷多少次,恰有
),并将每次的得分进行累记,他发现,不论采取怎样的投掷方案以及投掷多少次,恰有![]() 个分值总是记录不到,例如
个分值总是记录不到,例如![]() 就是其中之一,试确定
就是其中之一,试确定![]() 的值.
的值.
解:设此人掷得正面![]() 次,背面
次,背面![]() 次,则累计得分为
次,则累计得分为 ![]() ,若
,若 ![]() 则对任一个不能被
则对任一个不能被![]() 整除的正整数分值,他都记录不到,也就是有无穷多个数记录不到,所以
整除的正整数分值,他都记录不到,也就是有无穷多个数记录不到,所以
![]() . 现在设
. 现在设![]() 为掷币人能够记录到的一个分值,则方程
为掷币人能够记录到的一个分值,则方程 ![]() 至少有一组非负整解,(即直线
至少有一组非负整解,(即直线![]() 上至少有一整点位于闭的第一象限内),
上至少有一整点位于闭的第一象限内),
(1).若![]() ,因为
,因为![]() ,则
,则![]() 个正整数
个正整数![]() 构成模
构成模![]() 的完全剩余系,其中恰有一个是
的完全剩余系,其中恰有一个是![]() 的倍数,即此时方程
的倍数,即此时方程 ![]() 有非负整数解。也就是
有非负整数解。也就是![]() 能被记录到,因此掷币人能够记录到的分值
能被记录到,因此掷币人能够记录到的分值![]() 应满足:
应满足:![]() .
.
(2).当![]() ,因为
,因为![]() ,则直线
,则直线![]() 上至少有一整点位于闭的第一象限内,事实上,设闭的第一象限内有两个整点
上至少有一整点位于闭的第一象限内,事实上,设闭的第一象限内有两个整点![]() 在直线上,则直线
在直线上,则直线
![]() 的斜率
的斜率 ![]() 满足
满足 ![]() ,但由直线
,但由直线 ![]()
![]() ,则
,则
![]() ,而由截距,
,而由截距,![]() 知
知 ![]() 不是既约分数,矛盾。据此知,在
不是既约分数,矛盾。据此知,在
闭的第一象限内,满足![]() 的整点与满足
的整点与满足![]() 且可记录到的分值
且可记录到的分值![]() ,一 一对应,因为闭矩形
,一 一对应,因为闭矩形![]() 内有
内有![]() 个整点,故在
个整点,故在
闭的第一象限内,满足![]() 的整点数为
的整点数为![]() 个,从而满足
个,从而满足![]() 的
的![]() 个数值
个数值![]() 中,不能记录到的数值
中,不能记录到的数值![]() 的个数为:
的个数为:
![]() .
.
所以 ![]() ,由
,由![]()
![]() ,而
,而
![]() ,故仅有
,故仅有 ![]() 及
及 ![]() 可能适合;若取
可能适合;若取![]() ,则
,则
![]() 能够记录到,不合题意,再考察
能够记录到,不合题意,再考察 ![]() 上的整点,显然此方程没有非负整解,即分值
上的整点,显然此方程没有非负整解,即分值![]() 记录不到,因此
记录不到,因此![]() 是合于题意的唯一解.
是合于题意的唯一解.