2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题C (陶平生供题)
学校 姓名 营员证号
一、四面体ABCD,它的内切球O与面ABD切于E,与面BCD切于F,
证明:∠AEB=∠CFD.

二、如图,⊙O1、⊙O2、⊙O3分别外切⊙O于A1、B1、C1,并且前三个圆还分别与△ABC的两条边相切.
求证:三条直线AA1、BB1、CC1相交于一点.
三、设实数a≥b≥c≥d>0,求函数
![]() 的最小值.
的最小值.
四、n个白子A与n个黑子B(n≥3),依次不留间隙地排成一行:AA……ABB……B,现作如下操作:每次将相邻的两子取出(并保持此两子的先后次序),放在其它棋子旁的空位上(仍在同一行).
证明:经过n次这样的操作,可使它们排成黑白相间的一行,且不留间隙.
(附:当n=3时,操作如图所示)
初始状态 AAABBB
第一次操作后 ABBBAA
第二次操作后 ABB ABA
第三次操作后 BABABA
2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题C解答 (陶平生供题)
学校 姓名 营员证号
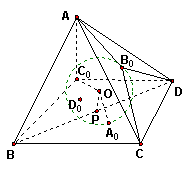 一、四面体ABCD,它的内切球O与面ABD切于E,与面BCD切于F,
一、四面体ABCD,它的内切球O与面ABD切于E,与面BCD切于F,
证明:∠AEB=∠CFD.
证明:为叙述方便,将内切球O在面![]() 上的切点分别改记为
上的切点分别改记为![]() ,于是,
,于是,![]() ,设球O的半径为
,设球O的半径为![]() ,棱
,棱![]() 面
面![]() ,设垂足为
,设垂足为![]() ,则
,则
![]() , 因为
, 因为 ![]() , 则
, 则 ![]()
![]() ,故
,故![]()
![]() ,所以
,所以 ![]() ,即是说,棱
,即是说,棱![]() 关于两相邻面上切点的张角相等.其它棱的情况与此类似。
关于两相邻面上切点的张角相等.其它棱的情况与此类似。
在![]() 中,设
中,设![]() ,则
,则 ![]() 1
1
于是,![]()
在![]() 中,设
中,设![]() ,因为
,因为 ![]() ,所以
,所以
![]() ,于是
,于是 ![]() 2
2
在![]() 中,
中,![]()
![]() ,设
,设 ![]() ,
,
则 ![]() 3
3
在![]() 中,
中,![]() ,
,![]()
则 ![]() 4
4
3+4得,![]() ,据此及2得,
,据此及2得,
![]() ,所以
,所以 ![]() 5
5
由 1、5得,![]() 故4式化为
故4式化为 ![]() ……6
……6
由 1、6得,![]() ,即
,即 ![]() ,也即
,也即
![]()
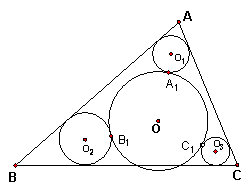 二、如图,⊙O1、⊙O2、⊙O3分别外切⊙O于A1、B1、C1,并且前三个圆还分别与△ABC的两条边相切.
二、如图,⊙O1、⊙O2、⊙O3分别外切⊙O于A1、B1、C1,并且前三个圆还分别与△ABC的两条边相切.
求证:三条直线AA1、BB1、CC1相交于一点.
证明:设![]() 及
及![]() 分别是四个圆的圆心,其半径分别为
分别是四个圆的圆心,其半径分别为![]() 与
与![]() ,
,![]() 的内切圆半径为
的内切圆半径为![]() ,显然,
,显然,![]() 为
为![]() 的三条内角平分线,故相交于其内心
的三条内角平分线,故相交于其内心![]() .设
.设![]() (定值).
(定值).
记![]() ,
,![]() ,对于
,对于![]() ,因为⊙O
,因为⊙O
与![]()
![]() 的切点
的切点![]() 在连心线
在连心线![]() 上,点
上,点![]() 在
在![]() 的延长线上,则直线
的延长线上,则直线![]() 必与线段
必与线段![]() 相交,其交点设为
相交,其交点设为![]() .
.
同理可设,直线 ![]() .只须证
.只须证![]() 重合.
重合.
 直线
直线![]() 截
截![]() 于
于![]() ,由梅尼劳斯定理,
,由梅尼劳斯定理,![]() ,
,
即
![]() 1
1
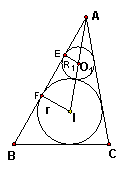 同理有
同理有![]() 2 ,以及
2 ,以及 ![]() 3
3
易知 ![]() ,所以
,所以 ![]() ,从而
,从而
![]() ,故
,故
![]() ,所以,
,所以,
![]() ,因此
,因此![]() 共点,即
共点,即![]() 交于一点.
交于一点.
三、设实数a≥b≥c≥d>0,求函数
![]() 的最小值.
的最小值.
解:显然![]() 没有上界,这是由于,当
没有上界,这是由于,当![]() 时,
时,![]() ,
,
又注意![]() 是一个零次齐次函数,且当
是一个零次齐次函数,且当![]() 时,
时,![]() 的值为
的值为![]()
以下证明,对于满足条件的任何正数![]() 均有
均有![]() ,即要证
,即要证
![]()
![]() ……1
……1
据条件,![]() 设
设 ![]()
则 ![]() 1式化为:
1式化为:
![]()
![]()
![]() ……2
……2
活化一个常量,改记1为![]() ,且设
,且设
![]()
![]()
则 ![]() 皆为
皆为![]() 的四次多项式,而
的四次多项式,而 ![]() 为
为![]() 的二次多项式.
的二次多项式.
记 ![]()
为证2式成立,即要证,![]() 于是只要证,
于是只要证,![]() ,
,![]() ,
,![]() .
.
易知,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
以上用到,![]() ,
,![]() ,以及
,以及
![]() .
.
![]() .
.
以上用到,![]() .
.
![]() .
.
故![]() .因此,函数
.因此,函数![]() 的最小值是
的最小值是![]() .
.
四、n个白子A与n个黑子B(n≥3),依次不留间隙地排成一行:AA……ABB……B,现作如下操作:每次将相邻的两子取出(并保持此两子的先后次序),放在其它棋子旁的空位上(仍在同一行).
证明:经过n次这样的操作,可使它们排成黑白相间的一行,且不留间隙.
(附:当n=3时,操作如图所示)
初始状态 AAABBB
第一次操作后 ABBBAA
第二次操作后 ABB ABA
第三次操作后 BABABA
证 :当![]()
![]() 时,对
时,对![]() 归纳:
归纳:
![]() 时, 初始状态为: AAAABBBB
时, 初始状态为: AAAABBBB
第一次操作后: A ABBBBAA
第二次操作后: ABBA BBAA
第三次操作后: ABBABAB A
第四次操作后: BABABABA
为表达方便,用数字![]() 表示“将自左向右数的第
表示“将自左向右数的第![]() 枚棋子取出,跨过某些棋子向右平移至最先出现的空位上”这一操作;而数字
枚棋子取出,跨过某些棋子向右平移至最先出现的空位上”这一操作;而数字![]() 表示“将自右向左数的第
表示“将自右向左数的第![]() 枚棋子取出,跨过某些棋子向左平移至最先出现的空位上”这一操作;于是,施于
枚棋子取出,跨过某些棋子向左平移至最先出现的空位上”这一操作;于是,施于![]() 对棋子的操作步骤
对棋子的操作步骤![]() 便可用一个
便可用一个![]() 元有序数组
元有序数组![]() 来表示.
来表示.
因此,![]() ,
,![]() ,
,
![]() ,…….
,…….
我们注意到,在![]() 中,都恰有一次操作“1”,即当全部操作完成后,棋子已黑白相间排列(以黑子B开头),且整行向右移动了两子的位置.
中,都恰有一次操作“1”,即当全部操作完成后,棋子已黑白相间排列(以黑子B开头),且整行向右移动了两子的位置.
以下证明,当![]() 时,
时,![]() 个相连的白子和
个相连的白子和![]() 个相连的黑子排成一行,可经
个相连的黑子排成一行,可经![]() 次移动两子的操作,使黑白相间(以黑子B开头),且整行向右移动了两子的位置.
次移动两子的操作,使黑白相间(以黑子B开头),且整行向右移动了两子的位置.
对![]() 归纳:当
归纳:当![]() 时,结论已成立,今设结论对于n成立,考虑n+4对棋子的情形,如有
时,结论已成立,今设结论对于n成立,考虑n+4对棋子的情形,如有![]() 对棋子黑白分段排列于一行(白子在前):
对棋子黑白分段排列于一行(白子在前):
AAAAA…AB…BBBBB
为此,采用“杠中开花”的办法,我们设想,先把中间加方框的![]() 对(
对(![]() 个)棋子收藏于一条“竖杠”中,成为四对棋子的一个排列:
个)棋子收藏于一条“竖杠”中,成为四对棋子的一个排列:
AAAA┃BBBB
现对这四对棋子进行![]() 中的前两步操作:
中的前两步操作:
第一次操作后: A A│BBBBAA
第二次操作后: ABBA┃ BBAA
经这两次操作后,中间(竖杠右侧)已出现两子空位,然后,对竖杠所代表![]() 对加方框的棋子进行
对加方框的棋子进行![]() 次操作,据归纳假设,可使黑白相间(加方框的棋子中,黑子B在前,且其前面有两子空位):
次操作,据归纳假设,可使黑白相间(加方框的棋子中,黑子B在前,且其前面有两子空位):
ABBA BABA…BABBAA
这![]() 次操作算作
次操作算作![]() 的第
的第![]() 次操作。再把加方框的
次操作。再把加方框的![]() 对棋子收藏于一条竖杠中,又成为四对棋子的排列(竖杠左侧有两子空位):
对棋子收藏于一条竖杠中,又成为四对棋子的排列(竖杠左侧有两子空位):
ABBA
┃BBAA,对图中的四对棋子进行![]() 的后两次操作,成为:
的后两次操作,成为:
ABBABA│B A
BABA│BABA
即得到黑白间隔排列(黑子在前,竖杠左侧的两子空位已被填充,整行无间隙.)
现恢复竖杠所代表![]() 对加方框的棋子,于是,上述两次操作就成为
对加方框的棋子,于是,上述两次操作就成为![]() 的第
的第![]() 次操作。且这
次操作。且这![]() 对棋子已黑白相间(黑子在前,整行无间隙,且右移了两子空位).
对棋子已黑白相间(黑子在前,整行无间隙,且右移了两子空位).
BABABA…BABABABA
据归纳法,知所证结论成立。