上海市高中数学实验班理科实验班入学测试

上海市2002年高中数学实验班理科实验班入学测试

数　学　试　卷

（满分150分，考试时间90分钟）

一、填空题（本大题满分80分，每小题8分）

1、　设x为满足x²⁰⁰²+2002²⁰⁰¹＝x²⁰⁰¹+2002²⁰⁰² 的整数，则x＝　　　　

2、　设m＝，则m的末两位数字为　　　　

3、　关于x、y的方程组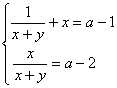恰有一组实数解，则实数a的值为　　　　 

4、　设f(x)为一次函数，满足：f(0)= -1，f(f(0))= -2，则f(2002)的值为　　　　

5、　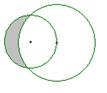依法纳税是每个公民的义务，依我国税法规定：月收入超过800元的部分需要交税（800元以内不交税），且根据超过部分的多少按不同的税率交税。不超过500元部分税率为5％；超过500元至2000元部分税率为10％；…某职员在2002年3月的应交税款为105元，则该职员在该月的税后收入为　　　 元。

6、　设n为正整数，且n³+2n²是一个奇数的平方，则满足条件的n中，最小的两个数之和为　　　　　

7、　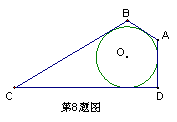如图所示，一个半径为的圆过一个半径为2的圆的圆心，则图中阴影部分的面积为　　　　 

8、　如图所示，四边形ABCD是某个圆的圆外切四边形，已知∠A＝∠B＝120°，∠D＝90°,且BC＝1，则AD的长为　　　　

9、　设n为不小于2的正整数，记n的所有正约数（包括1和n）的乘积为P(n),已知P(n)=n¹²，则n的最小值为　　　　 

10、　　　　　　  已知从1，2，…，9中可以取出m个数，使得这m个数中任意两个数之和不相等，则m的最大值为　　　　

二、解答题（本大题满分70分，共4个小题）

11、　　　　　　  （本题14分）已知关于x，y的方程组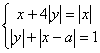恰有两组解，求实数a的取值范围。

12、　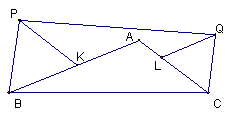　　　　　  （本题16分）在△ABC中，∠A＝120°，K、L分别是AB、AC上的点，向△ABC的形外作正三角形BKP和CLQ。证明：

13、　　　　　　  （本题20分）问：在8×8的国际象棋盘上最多可以放多少个“+”字形（其中每个“+”字形占据棋盘的5个小方格），使得任意两个“+”字形不重叠，且每个“+”字形都不超出棋盘的边界？证明你的结论。

14、　　　　　　  （本题20分）求所有的二次函数f(x)=x²-ax+b，这里a、b为整数，且存在三个取自1，2，…，9的不同整数m、n、p，使得