2006年高考“排列、组合与二项式定理”试题
1．（2006年福建卷）
展开式中
的系数是＿10＿（用数字作答）。
2．（2006年广东卷）在
的展开式中，
的系数为
3．
所以的系数为
4．（2006年陕西卷）
展开式中
的常数项为＿594＿（用数字作答）。
5．某校从8名教师中选派4名教师同时去4个边远地区支教（每地1人），其中甲和乙不同去，甲和丙只能同去或同不去，则不同的选派方案共有＿＿600＿种（用数字作答）。
6．( 2006年重庆卷)若
n的展开式中各项系数之和为64，则展开式的常数项为 (
A)
(A)-540 (B)
(c)162 (D)540
7．( 2006年重庆卷)将5名实习教师分配到高一年级的３个班实习，每班至少１名，最多２名，则不同的分配方案有 ( B )
（A）３０种 （B）９０种
（C）１８０种 （D）２７０种
8. （2006年上海春卷）电视台连续播放6个广告，其中含4个不同的商业广告和2个不同的公益广告，要求首尾必须播放公益广告，则共有 48 种不同的播放方式（结果用数值表示）.
9．（2006年全国卷II）在(x4＋)10的展开式中常数项是 45 （用数字作答）
10．（2006年天津卷）将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有（ A ）
A．10种 B．20种 C．36种 D．52种
11．（2006年天津卷）
的二项展开式中
的系数是____280 （用数学作答）．
12. （2006年湖北卷）在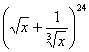
的展开式中，的幂的指数是整数的项共有 （C）
A.3项 B.4项 C.5项 D.6项
12．解选C 。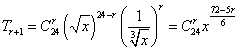
，∴
，即
。而
。
∴
。
13. （2006年湖北卷）某工程队有6项工程需要先后单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在工程乙完成后进行，又工程丁必须在丙完成后立即进行，那么安排这6项工程的不同的排法种数是__20________.（用数字作答）
13．解填20.考查有条件限制的排列问题，其中要求部分元素间的相对顺序确定；据题意由于丁必需在丙完成后立即进行，故可把两个视为一个大元素，先不管其它限制条件使其与其他四人进行排列共有
种排法，在所在的这些排法中，甲、乙、丙相对顺序共有
种，故满足条件的排法种数共有
。
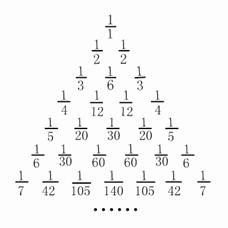14. （2006年湖北卷）将杨辉三角中的每一个数
都换成分数
，
就得到一个如右图所示的分数三角形，称为莱布尼茨三角形. 从莱布尼茨三角形可以看出
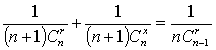，其中
=__ r＋1__.
令
，
则
=__1/2__.
14．解填r＋1, 1/2.本题考查考生的类比归纳及推理能力，第一问对比杨辉三角的性质通过观察、类比、归纳可知莱布尼茨三角形中每一行中的任一数都等于其“脚下”两数的和，故此时
，第二问实质上是求莱布尼茨三角形中从第三行起每一行的倒数第三项的和，即
根据第一问所推出的结论只需在原式基础上增加一项
，则由每一行中的任一数都等于其“脚下”两数的和，结合给出的数表可逐次向上求和为
，故
，从而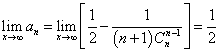
。
15．（2006年全国卷I）设集合
。选择I的两个非空子集A和B，要使B中最小的数大于A中最大的数，则不同的选择方法共有
A．
B．
C．
D．
15．显然
，设
，则C是I的非空子集，且C中元素不少于2个（当然，也不多于5个）。
另一方面，对I的任何一个k（
）元子集C，我们可以将C中元素从小到大排列。排好后，相邻数据间共有k
1个空档。在任意一个空挡间插入一个隔板，隔板前的元素组成集合A，隔板后元素组成集合B。这样的A、B一定符合条件，且集合对{A，B}无重复。
综合以上分析，所求为：
。选B。
16．（2006年全国卷I）安排7位工作人员在5月1日到5月7日值班，每人值班一天，其中甲、乙二人都不能安排在5月1日和2日，不同的安排方法共有___2400______种。（用数字作答）
16．这个题有点文字游戏的味道。“都不”是全部否定，即：甲不在，乙也不在。如果换成“不都”，那就成部分否定了，即：只要有一人不在。
“都不”：用乘法原理，把3、4、5、6、7五天“拿出来”，先让甲选值班日期，有5种选法；接下来让乙选值班日期，有4种选法。再接下来5名工作人员任意排，有
种排法。综合以上分析，不同的安排办法共有
种。
“不都”：从集合的观点来看，“都”的补集就是“不都”（而不是“都不”），因此从反面去想来的最简单 —— 从全部中剔除“都”即可。7人任意安排在7天内值班，有
种安排办法，其中甲、乙都在1、2号中某天值班的安排办法有
种。计算
。
从结果上来看，“都不”的结果要比“不都”的结果小。这是当然的！图2反映了全集中“都”、“不都”、“都不”之间的关系。
17．（2006年江苏卷）今有2个红球、3个黄球、4个白球，同色球不加以区分，将这9个球排成一列有 ▲ 种不同的方法（用数字作答）。
解：由题意，
点评：本题主要考查不全相异元素的全排列
18．（2006年江苏卷）
的展开式中含x的正整数指数幂的项数是
（A）0 （B）2 （C）4 （D）6
解：展开式通项为
，若展开式中含x的正整数指数幂，即
所以
，选（B）
点评：本题主要考查二项式定理的相关知识
19．（2006年江西卷）在（x－
）2006 的二项展开式中，含x的奇次幂的项之和为S，当x＝时，S等于（B ）
A.23008 B.-23008 C.23009 D.-23009
解：设（x－）2006＝a0x2006＋a1x2005＋…＋a2005x＋a2006
则当x＝时，有a0（）2006＋a1（）2005＋…＋a2005（）＋a2006＝0 （1）
当x＝－时，有a0（）2006－a1（）2005＋…－a2005（）＋a2006＝23009 （2）
（1）－（2）有a1（）2005＋…＋a2005（）＝－23009¸2＝－23008
故选B
20．（2006年辽宁卷）5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.(以数作答)
【解析】两老一新时, 有
种排法;
两新一老时, 有
种排法,即共有48种排法.
【点评】本题考查了有限制条件的排列组合问题以及分类讨论思想.
21．（2006年北京卷）在
这五个数字组成的没有重复数字的三位数中，各位数字之和为奇数的共有(B)
（A）36个 （B）24个
（C）18个 （D）6个
22．（2006年北京卷）在
的展开式中，
的系数中_______-14___________（用数字作答）.
23．（2006年上海卷）如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 36 ．
24．（
2006年浙江卷）若多项式
( D )
(A)9 (B)10 (C)-9 (D)-10
25．（
2006年浙江卷）函数f:1,2,3
1,2,3满足f(f(x))= f(x)，则这样的函数个数共有 ( D )
(A)1个 (B)4个 (C)8个 (D)10个
26. ( 2006年湖南卷）过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有 ( D )
A.4条 B.6条 C.8条 D.12条
27. ( 2006年湖南卷）某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有 ( D )
A.16种 B.36种 C.42种 D.60种
28. ( 2006年湖南卷）若
的展开式中
的系数是-80,则实数
的值是 -2 .
29．(2006年山东卷）已知集合A=｛5｝,B=｛1,2｝,C=｛1,3,4｝，从这三个集合中各取一个元素构成空间直角坐标系中点的坐标，则确定的不同点的个数为 (A)
(A)33 (B) 34 (C) 35 (D)36
30．(2006年山东卷）已知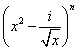
的展开式中第三项与第五项的系数之比为－
,其中
=－1，则展开式中常数项是 (
D)
(A)－45i (B) 45i (C) －45 (D)45