07届高三数学模拟试题二
一.选择题(每题5分,共50分)
1.若条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的
的
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分又不必要条件
2.平面向量中,向量
![]() ,
,![]() ,则下列关于
,则下列关于![]() ,
,![]() 的4个命题中正确的有几个
(1)
的4个命题中正确的有几个
(1)![]() 在
在![]() 上的投影为
上的投影为![]() ; (2)与
; (2)与![]() ,
,![]() 的夹角相等的向量为
的夹角相等的向量为![]()
![]() ;
;
(3)任意非零向量![]() 与
与![]() ,
,![]() 的夹角之和为定值;
的夹角之和为定值;
(4)![]() 轴上任意一点(非原点)到
轴上任意一点(非原点)到![]() 与到
与到![]() 的距离之比为1:2.
的距离之比为1:2.
A. 0 B. 1 C. 2 D. 3
3.在下列函数中,满足性质:“对于(1,2)上的任意![]()
![]() 恒成立”的只有
恒成立”的只有
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
4. 当实数![]() 满足
满足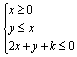 (
(![]() 为常数)时,
为常数)时,![]() 有最大值12,则实数
有最大值12,则实数![]() 的值是
的值是
A. - 12 B.- 9 C. 9 D. 12
5.数列![]() 中,
中,![]() 是公比为
是公比为![]() 的等比数列,满足,
的等比数列,满足,![]()
![]()
![]() ,则公比
,则公比![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.从1、2、3、4、5、6、7共7个数字任取两个数字,则用这两个数可以组成两位奇数的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
7.已知正四面体![]() 中,
中,![]() ,则直线
,则直线![]() 所成的角是
所成的角是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
8.在等差数列![]() 中,
中,![]() ,
,![]() 为常数,且
为常数,且![]() ,若对任意
,若对任意![]() 都有
都有![]() 成立,则
成立,则![]() 的范围是
的范围是
A.![]() 且
且![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
9.已知点![]() 在曲线
在曲线![]() 上,则
上,则![]() (
(![]() 为坐标原点)的最小值为 A.
为坐标原点)的最小值为 A. ![]() B.
B. ![]() C.
C. ![]() D.1
D.1
10.![]() 中 ,
中 ,![]()
![]() ,
,![]() 是
是![]() 边上的点,且
边上的点,且![]() 到
到![]() 的距离的乘积为
的距离的乘积为![]() ,这样的点
,这样的点![]() 共有
共有
A. 0个 B.1个 C.2个 D.无数个
二.填空题(每题5分,共30分)
11.计算: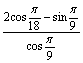 =
=
12.将下面的平面图形(其中每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四
面体,则直线![]() 是异面直线的是
是异面直线的是

(1) (2) (3) (4)
13.某班有40人,其中甲组18人,平均成绩为90分,标准差为6;乙组22人,平均成绩为80分,标准差为4,则全班成绩的标准差为
14.过![]() 的重心
的重心![]() 的动直线分别交
的动直线分别交![]() 于
于![]() ,若
,若![]() ,则
,则![]() 的面
的面
积与![]() 的面积比的范围是
的面积比的范围是
15.若正数![]() 满足
满足![]() 时恒有
时恒有![]() ,则参数
,则参数![]() 的最大值为
的最大值为
16.函数![]() 的值域为
的值域为
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
三.解答题
17. (本小题满分12分)完成以下问题的解答过程:
某种产品的总成本![]() (元)是产量
(元)是产量![]() (件)的函数且
(件)的函数且![]() ,试问:当
,试问:当![]() 时,从降低单位成本的角度考察,试问:继续生产是否得当?
时,从降低单位成本的角度考察,试问:继续生产是否得当?
解:当![]() 元时,总成本
元时,总成本![]() = 元,
= 元,
这时单位产品的平均成本![]() (元/件),
(元/件),
因为边际成本![]() ,所以边际成本
,所以边际成本![]() (元/件) .
(元/件) .
即此时再生产一件产品仅需 元,
因此加进这件产品时, 平均成本得到 (填下降或上升) ,
故该企业 继续生产 (填应该或不应该) .
(18). (本小题满分14分)如图,在四棱锥![]() 中,底
中,底
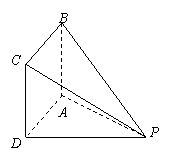 面
面![]() 是边长为
是边长为![]() 的正方形,且
的正方形,且![]()
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
19. (本小题满分14分)设函数![]() 的图象为
的图象为![]()
![]() 的图象为
的图象为![]() ,且
,且![]() 关于点
关于点![]() 对称.
对称.
(1) 函数![]() 是否有对称中心,若有,求出对称中心;若没有,请说明理由.
是否有对称中心,若有,求出对称中心;若没有,请说明理由.
(2)求![]() 的表达式.
的表达式.
(3)解不等式![]() ,
,![]() .
.
20.(本小题满分14分)已知![]() 是椭圆
是椭圆![]() 的两个焦点,过
的两个焦点,过![]() 的直线与椭圆
的直线与椭圆![]()
的两个交点为![]() ,且
,且![]() 的最小值为6.
的最小值为6.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的长轴顶点.当
的长轴顶点.当![]() 取最小值时,求
取最小值时,求![]() 的大小.
的大小.
21.(本小题满分16分)在直角坐标系上有一点列![]() 对每个正整数
对每个正整数![]() ,点
,点![]() 位于函数
位于函数![]()
![]() 的图象上,且点
的图象上,且点![]() 、点
、点![]() 与点
与点![]() 是以
是以![]() 为顶角的等腰三角形的三个顶点。
为顶角的等腰三角形的三个顶点。
(1)求点![]() 的纵坐标
的纵坐标![]() 的表达式;
的表达式;
(2)若对每个正整数![]() ,以
,以![]() ,
,![]() ,
,![]() 为边长能构成一个三角形,求
为边长能构成一个三角形,求![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() 取(2)中确定的范围内的最小的整数,问数列
取(2)中确定的范围内的最小的整数,问数列![]() 中第几项最大。
中第几项最大。