07级高三综合训练文科数学试题

07级高三综合训练文科数学试题

一．选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.　　 已知集合，，则集合P∩Q等于
A．　　　　　　　B．　　　　　　 C．　　D．

2.　　 到两定点A(0，0)，B(3，4)距离之和为5的点的轨迹是
A．椭圆　　　　　　　　　　　　　　 B．直线AB　　　　　　　C．线段AB　　　　　　D．无轨迹

3.　　 右图为函数的图象，其中m、n为常数，则下列结论正确的是
A．m < 0，n > 1　　　　　　　　 B．m > 0，n > 1
C．m > 0，0 < n < 1　　　　　D．m < 0，0 < n < 1

4.　　 设a、b、c是互不相等的正数，则下列等式中不恒成立的是
A． a－b ≤ a－c + b－c 　　　　　　　　　　　　　　　B．≤
C．≥2　　　　　　　　　　　　　　　　　　　　　D．≥2

5.　　 下列函数中，在其定义域内既是奇函数又是减函数的是
A． (x∈R)　　　　　 B． (x∈R)　C． (x∈R)　　D． (x∈R)

6.　　 正方体ABCD－A₁B₁C₁D₁中，E、F分别是CC₁、C₁D₁的中点，则异面直线EF和BD所成的角的大小为
A．75°　　　　　　　　　　　　　　 B．60°　　　　　　　　　　C．45°　　　　　　　　　D．30°

7.　　 某路段检查站监控录象显示，在某时段内，有1000辆汽车通过该站，现在随机抽取其中的200辆汽车进行车速分析，分析的结果表示为如右图的频率分布直方图，则估计在这一时段内通过该站的汽车中速度不小于90km/h 的约有
A．100辆　　　　　　　　　　　　　B．200辆
C．300辆　　　　　　　　　　　　 D．400辆

8.　　 设，(0，1)，则满足条件0≤≤1，0≤≤1的动点P的变化范围(图中阴影部分含边界)是

9.　　 若两个函数的图像经过若干次平移后能够重合，则称这两个函数为“同形”函数．给出下列三个函数：，，，则
A．为“同形”函数
B．为“同形”函数，且它们与不为“同形”函数
C．为“同形”函数，且它们与不为“同形”函数
D．为“同形”函数，且它们与不为“同形”函数

10.  在某次数学测验中，学号i (i = 1，2，3，4)的四位同学的考试成绩f (i)∈{90，92，93，96，98}，且满足f (1) < f (2) < f (3) < f (4)，则这四位同学的考试成绩的所有可能情况的种数为
A．15种　　　　　　　　　　　　　　B．10种　　　　　　　　　 C．5种　　　　　　　　　 D．4种

二．填空题：本大题共5小题，每小题5分，共25分。将正确答案填在答题卷上对应题号的横线上。

11.  的展开式中常数项是　▲　．

12.  已知等比数列{a_n}中，，则它的前15项的和S₁₅ =　▲　．

13.  若一条曲线既是轴对称图形又是中心对称图形，则我们称此曲线为“双重对称曲线”．有下列四条曲线：
　　①；②；③；④．
其中是“双重对称曲线”的序号是　▲　．

14.  某商场在节假日对顾客购物实行一定的优惠，商场规定：
①如一次购物不超过200元，不给予折扣；
②如一次购物超过200元不超过500元，按标价给予九折(即标价的90%)优惠；
③如一次购物超过500元的，其中500元给予九折优惠，超过500元的剩余部分给予八五折优惠．
某人两次去购物，分别付款176元和432元，如果他只去一次购买同样的商品，则他应该付款为　▲　元．

15.  设函数，给出下列命题：
①f (x)有最小值；
②当a = 0时，f (x)值域为R；
③当a > 0时，f (x)在［2，+∞)上有反函数；
④若f (x)在区间［2，+∞)上单调递增，则实数a的取值范围是a≥－4．
其中真命题的序号为　▲　．

三．解答题：本大题共6小题，满分75分。解答应写出文字说明，证明过程或演算步骤。

16.　　 (本大题满分12分)设，已知，，其中．
(1)若，且a = 2b，求的值；
(2)若，求的值．

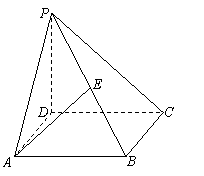
17.　　 (本大题满分12分)如图，在四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD = AB = a，E是PB的中点，F为AD中点．
(1)求异面直线PD、AE所成的角；
(2)求证：EF⊥平面PBC．
(3)求二面角F－PC－E的大小．

18.　　 (本大题满分12分)已知10件产品中有3件是次品．
(1)任意取出3件产品作检验，求其中至少有1件是次品的概率；
(2)为了保证使3件次品全部检验出的概率超过0.6，最少应抽取几件产品作检验？

19.　　 (本大题满分12分)在平面直角坐标系中，已知点A(1，0)，向量e = (0，1)，点B为直线上的动点，点C满足，点M满足，．
(1)试求动点M的轨迹E的方程；
(2)试证直线CM为轨迹E的切线．

20.　　 (本大题满分13分)已知函数，当x∈[a₁，b₁]时f (x)的值域为[a₂，b₂]，当x∈[a₂，b₂]时f (x)的值域为[a₃，b₃]，…，依次类推，一般地，当x∈[a_n－1，b_n－1]时f (x)的值域为[a_n，b_n]，其中a、b为常数，a₁ = 0，b₁ = 1．
(1)若a = 1，求数列{a_n}、{b_n}的通项公式；
(2)若a < 0，求证：是等比数列；
(3)若a < 0，设数列{a_n}、{b_n}的前n项和分别为S_n、T_n，求
…+ S_n)的值．

21.　　 (本大题满分14分)已知函数，，h (x) = kx + 9，又f (x)在x = 2 处取得极值9．
(1)求a、b的值；
(2)如果当时，f (x)≤h (x)≤g (x)恒成立，求k的取值范围．