07届高三数学试卷(二)
参考公式:
三角函数的和差化积公式
sinα+sinβ=2sincos sinα-sinβ=2 cossin
cosα+cosβ=2coscos cosα-cosβ=-2sinsin
若事件A在一次试验中发生的概率是p,则在n次独立重复试验中恰发生k次的概率:
Pn(k)=C pk(1-p)n-k
数据x1,x2,…,xn的方差为s2=[( x1-)2+( x2-)2+( xn-)2],为平均数.
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知命题“![]() ”,命题“
”,命题“![]() ”,如果“
”,如果“![]() 且
且![]() ”与“非
”与“非![]() ”都为假命题,
”都为假命题,
则满足条件的![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.设![]() 为两两不重合的平面,
为两两不重合的平面,![]() 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]()
③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() .
.
其中,真命题的个数是( )
A.1 B.2 C.3 D.4
3.数列![]() 的前
的前![]() 项和
项和![]() ,则
,则![]() ( )
( )
A.350 B.351 C.337 D.338
4.有一笔统计资料,共有11个数据如下: 2、4、4、5、5、![]() 、6、7、8、9、11(不完全依大小排列),已知这组数据平均数为6,则这组数据的方差为( )
、6、7、8、9、11(不完全依大小排列),已知这组数据平均数为6,则这组数据的方差为( )
 A.6 B.
A.6 B.![]() C.
C.![]() D.
D.![]()
5.编号为A、B、C、D、E的5种蔬菜种在如右图所示的五块实验田里:每块只能种一种蔬菜,要求A品种不能种在1,2试验田里,B品种必须与A种在相邻的2块田里,则不同的种植方法有( )
A.42 B.36 C.32 D.30
6.设双曲线![]() ,离心率
,离心率![]() ,则两条渐近线夹角的取值范围是( )
,则两条渐近线夹角的取值范围是( )
A.![]() B
B![]() C.
C.![]() D.
D.![]()
7.已知向量![]() ,则向量
,则向量![]() 的模取最小值时,实数
的模取最小值时,实数![]() 的取值与
的取值与
![]() 的最小值分别是( )
的最小值分别是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 8.如图,三棱柱
8.如图,三棱柱![]() 的各棱长均为
的各棱长均为![]() ,
,![]() ,且侧面
,且侧面![]() 底面
底面![]() ,则直线
,则直线![]() 与平面
与平面![]() 所成的角为( )
所成的角为( )
A. 450 B.300 C.600 D.900
9.设偶函数![]() 在
在![]() 上递增,则
上递增,则![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]()
C.![]() D.不能确定
D.不能确定
|
|
|
|
|
|
|
|
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共6小题,每小题5分,共30分。
11.圆心在直线![]() 上,且与
上,且与![]() 轴相切于
轴相切于![]() 的圆的方程是_______________.
的圆的方程是_______________.
12.函数![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]() 的取值范围是_______
的取值范围是_______
13.![]() =_________.
=_________.
14.定义![]() 的数表平方运算规则是:
的数表平方运算规则是:
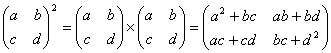 ,则
,则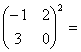 _________.
_________.
15.已知![]() ,且
,且![]() ,那么下列不等式
,那么下列不等式
①![]() ②
②![]() ③
③![]() ④
④![]()
 其中,正确的序号是____________.
其中,正确的序号是____________.
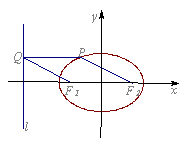
16.如图,设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,准线为
,准线为![]() ,P为椭圆上一点,PQ
,P为椭圆上一点,PQ![]() 于点Q,若四边形
于点Q,若四边形![]() 为平行四边形,则椭圆离心率的取值范围是_________
为平行四边形,则椭圆离心率的取值范围是_________
三、解答题:本大题共5小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最值;
的最值;
(2)将![]() 的图象按向量
的图象按向量![]() 平移,得到函数
平移,得到函数![]() 的图象,若
的图象,若![]() 为偶函数,求
为偶函数,求![]() 的最小正值.
的最小正值.
18.(本小题满分14分)某人射击一活动目标,射中目标的概率为![]() ,每次射击相互独立,连续射击20次.
,每次射击相互独立,连续射击20次.
(1)求至少射中一次的概率;
(2)记射中偶数次(包括0次)的概率和为![]() ,射中奇数次的概率和为
,射中奇数次的概率和为![]() ,求
,求![]() ;
;
 (3)求
(3)求![]() 的末四位数.
的末四位数.
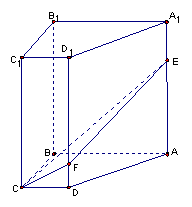
19. (本小题满分14分)如图,直四棱柱![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 上的点,且
上的点,且![]() .
.
(1)求直线![]() 与平面
与平面![]() 所成的角;
所成的角;
(2)求证:平面![]() 平面
平面![]() .
.
20. (本题满分14分)设椭圆![]() 的两个焦点
的两个焦点![]() ,且椭圆上存在点
,且椭圆上存在点![]() ,使得
,使得![]() .
.
(1)若点![]() 为椭圆短轴端点,求实数
为椭圆短轴端点,求实数![]() 的值与椭圆方程;
的值与椭圆方程;
(2)若点![]() 为椭圆上任意一点,求实数
为椭圆上任意一点,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,是否存在斜率为
,是否存在斜率为![]()
![]() 的直线
的直线![]() ,与椭圆交于不同的两点
,与椭圆交于不同的两点![]() 满足
满足![]() ,且过
,且过![]() 两点的直线
两点的直线![]() 满足
满足![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
21.(本题满分16分)已知曲线![]() ,过C上一点
,过C上一点![]() ,作一斜率为
,作一斜率为![]() 的直线,交曲线C于另一点
的直线,交曲线C于另一点![]() ,其中
,其中![]() .
.
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)求证:数列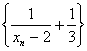 是等比数列;
是等比数列;
(3)![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 为偶数时,证明:
为偶数时,证明:![]()