2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题D
学校 姓名 营员证号
一 . 求证: ![]() 中有无穷多个平方数.
中有无穷多个平方数.
二 .
求所有函数![]() ,在零点连续 ,且
,在零点连续 ,且
![]()
三 . 如果素数p和自然数n满足 ![]() ,
,
证明: ![]()
四 . 设ABCD为凸四边形, AC交BD于P ,![]() 的内心依次为
的内心依次为![]() .
.
求证: ![]() 四点共圆当且仅当四边形ABCD有内切圆.
四点共圆当且仅当四边形ABCD有内切圆.
2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题D解答
学校: 姓名: 营员证号:
1.
求证:![]() 中有无穷多个平方数.
中有无穷多个平方数.
引理: ![]() 有无穷多组正整数解.
有无穷多组正整数解.
证明:首先有![]() .令
.令![]() .设(u,v)是
.设(u,v)是![]() 的一组正整数解,则若
的一组正整数解,则若![]() .令
.令
![]() ,则
,则![]() =
=![]()
显然.![]() ,故
,故![]() 有无穷多组正整数解.引理得证.
有无穷多组正整数解.引理得证.
取足够大的N,使得![]() 时,
时,![]()
考虑![]() .
.
![]()
![]()
![]()
![]()
所以 ![]() .
.
![]() 为完全平方数.证毕!
为完全平方数.证毕!
2.
求所有函数![]() ,在零点连续,且
,在零点连续,且
![]() (*)
(*)
解:令 ![]() (1)
(1)
![]()
![]()
而![]()
所以 f (0)=0
由(1)有 f(2f(y))=y+f(y)
(2)
在(*)中令 ![]() 故 f(f(y)=f(
故 f(f(y)=f(![]() f(y))+y+f(y)
f(y))+y+f(y)
再在(*)中令 y=![]() f(x)
f(x+2f(f(
f(x)
f(x+2f(f(![]() x))=f(f(
x))=f(f(![]() x))
x))
由(*)中f(x)为单射,故x+2f(![]() f(x))=
f(x))= ![]() f(x),
f(x),
将x换成y,有![]()
![]() (2')
(2')
![]() (3)
(3)
所以由(2)有 f(4f(f(y)))=f(2f(2f(y)))=2f(y)+f(2f(y))=2f(y)+2f(f(y))=3f(y)+y
另一方面
f(4f(f(y))=f(2(y+f(y))=f(2y)+y+f(y)
所以 f(2y)=2f(y) (4)
故由(*)及(4)有 f(x+f(2y))=f(x+2f(y))=f(x)+y+f(y)=f(x)+2f(f(y))=f(x)+f(f(2y))
所以 f(x+
f(y))= f(x)+ f(f(y))
(5)
于是,易知: f(kf(y))=kf(f(y))
![]() f(ky+y+f(y))= f((k+1)y) +f(f(y))= f(ky+f(f(2y)))=
f(ky+y+f(y))= f((k+1)y) +f(f(y))= f(ky+f(f(2y)))=![]()
=![]() 所以
所以
f((k+1)y)= f(ky) +f(y) ![]() f(ky)=kf(y)
f(ky)=kf(y)
![]()
![]() 当
当![]() 时,亦有 f(ky)=kf(y)
(6)
时,亦有 f(ky)=kf(y)
(6)
![]() (由(2'))
(由(2'))
![]()
![]()
所以 f(x+y)= f(x + f(2 f(y)![]() y))
(由(5))
y))
(由(5))
= f(x) + f(y)
由于f(x)在零点连续,所以f(x)在所有点连续,故
f(x)=cx (c为常数)
解得
c=1或![]()
所以 ![]()
经检验均满足条件.
3.
如果素数p和自然数n满足![]() ,证明:
,证明:![]() .
.
证明:引理: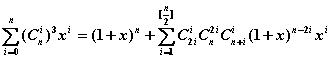
引理的证明 ,只要证明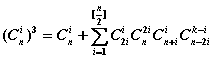
而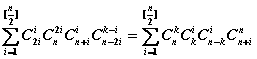 =
=![]() (李善兰恒等式)
(李善兰恒等式)
=![]() 引理证毕.
引理证毕.
对原命题:![]() 中
中![]() 的系数
的系数
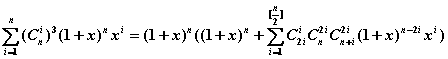
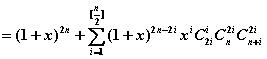

因 ![]()
故![]() 无素数因子p,而
无素数因子p,而![]()
故![]() 中必有一数大于p,从而
中必有一数大于p,从而 ![]() ,故
,故
![]() ,又
,又![]() .证毕.
.证毕.
4.  设ABCD为凸四边形,AC交BD于P.
设ABCD为凸四边形,AC交BD于P.![]() 的内心依次为
的内心依次为![]() .求证:
.求证:![]() 四点共圆当且仅当ABCD有内切圆.
四点共圆当且仅当ABCD有内切圆.
证明: 先证明必要性.当![]() 四点共圆时,
四点共圆时,
![]() (1)
(1)
设PA=x, PB=y, PC=z,
PD=w.
AB=a, BC=b,
CD=c, DA=d.![]()
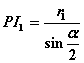 (
(![]() 为
为![]() 的半径)
的半径)
从而可知(1)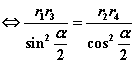
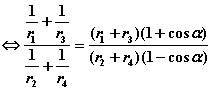 (2)
(2)
![]()
![]()
故(2)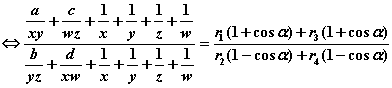
![]() (3)
(3)
设a+c![]() ,则
,则 ![]()
因为 ![]()
故 ![]()
![]()
![]()
(![]()
![]()
![]()
由(3)式,有:
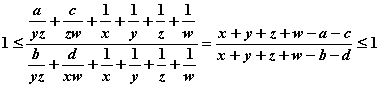
![]() 它们均等于1,
它们均等于1,![]() .必要性证毕.
.必要性证毕.
充分性.由上述证明可以知道
![]()
![]() ,从而(2)成立.
,从而(2)成立.
得出![]() 四点共圆,证毕.
四点共圆,证毕.