2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题A
学校: 姓名: 营员证号:____
 一.在
一.在![]() 中,a+c=3b,内心为I,内切圆在AB,BC边上的切点分别为D,E。设K是D关于点I的对称点,L是E关于点I的对称点.
中,a+c=3b,内心为I,内切圆在AB,BC边上的切点分别为D,E。设K是D关于点I的对称点,L是E关于点I的对称点.
求证:A,C,K,L四点共圆。
二.设![]() ,且对任意
,且对任意![]() 都有
都有
![]() │
│![]()
证明:![]()
三.求函数![]() 满足:
满足:
![]() 以及
以及
│![]() │
│![]() │
│![]() │,
│,![]()
四.设![]() !,能否把1到
!,能否把1到![]() 的正整数摆在一个圆周上,使得我们沿着顺时针方向移动时,每一个数都能按如下的法则由前一个数得到:或者把它加上17,或者加上28,如果必要的话,它可以减去
的正整数摆在一个圆周上,使得我们沿着顺时针方向移动时,每一个数都能按如下的法则由前一个数得到:或者把它加上17,或者加上28,如果必要的话,它可以减去![]() ?
?
2005年中国东南地区数学奥林匹克冬令营赛前培训
测试题A解答
学校: 姓名: 营员证号:____
一. 在![]() 中,a+c=3b,内心为I,内切圆在AB,BC边上的切点分别为D,E, 设K是D关于点I的对称点,L是E关于点I的对称点.
中,a+c=3b,内心为I,内切圆在AB,BC边上的切点分别为D,E, 设K是D关于点I的对称点,L是E关于点I的对称点.
求证:A,C,K,L四点共圆.
证:设直线BI交![]() 的外接圆点P,易知P是
的外接圆点P,易知P是![]() 的中点。记AC的中
的中点。记AC的中
为M,则PM![]() AC。设P在直线DI的射影为N
AC。设P在直线DI的射影为N
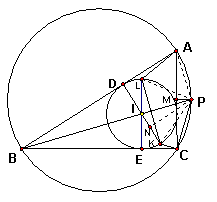 由于
由于![]() 则半周长
则半周长![]() ,
,
则![]()
又![]()
所以![]() ∽
∽![]() ,且相似比为2
,且相似比为2
熟知;![]() 。又
。又![]() ∽
∽![]() ,
,
所以![]() ,即N是IK的中点
,即N是IK的中点
进而![]() ,
,
所以![]() 都在以P为圆心的同一个圆周上
都在以P为圆心的同一个圆周上
二. 设![]() ,且对任意
,且对任意![]() 都有
都有
![]() │
│![]()
证明:![]()
证:假设![]() ,则
,则![]()
取素数![]() ,又取
,又取![]()
由费马小定理![]() ,从而
,从而![]()
进而![]() ,即
,即![]()
但![]() ,矛盾
,矛盾
三.求函数![]() 满足:
满足:
![]() 以及
以及
│![]() │
│![]() │
│![]() │,
│,![]()
解:取![]() 得
得![]()
![]() 时,可改写为:
时,可改写为:![]()
特别地,对任意![]() ,及
,及![]() ,有
,有![]() :
:
则![]()
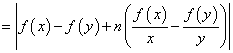
从而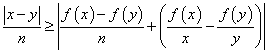
令![]() ,得
,得![]()
即![]()
四. 设![]() !,能否把1到
!,能否把1到![]() 的正整数摆在一个圆周上,使得我们沿着顺时针方向移动时,每一个数都能按如下的法则由前一个数得到:或者把它加上17,或者加上28,如果必要的话,它可以减去
的正整数摆在一个圆周上,使得我们沿着顺时针方向移动时,每一个数都能按如下的法则由前一个数得到:或者把它加上17,或者加上28,如果必要的话,它可以减去![]() ?
?
解:不能!假设存在合乎要求的摆法。
将![]() 按题述“运算”变为
按题述“运算”变为![]() ,筒记为:
,筒记为:![]()
题中运算是指取模![]() 的最小正剩余。
的最小正剩余。
若![]() ,则不可能有:
,则不可能有:![]()
否则圆周出现重复的数,故必有;![]()
进而![]()
若![]() ,类上知必有
,类上知必有![]()
这表明:当![]() 时,对
时,对![]() ,作同一种运算。
,作同一种运算。
由于在任何12个相连放在圆周上的数中,必有两个数模11同余,
设![]() ,从
,从![]() 到
到![]() 作了s次运算
作了s次运算![]() ,由前所述易知所作运算以s为周期
,由前所述易知所作运算以s为周期
取一个周期,将所有s个加数相加的和记为![]() ,则
,则![]()
故![]() ︱
︱![]()
则经![]() 次运算后,所得数与开始时的数相同,但
次运算后,所得数与开始时的数相同,但![]() <
<![]() ,矛盾!
,矛盾!