重庆南开中学高2006级2005-2006学年度2月月考
数学试题(理 科)
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.函数![]() 是
是
A.周期为![]() 的奇函数
B.周期为
的奇函数
B.周期为![]() 的偶函数
的偶函数
C.周期为![]() 的奇函数 D.周期为
的奇函数 D.周期为![]() 的偶函数
的偶函数
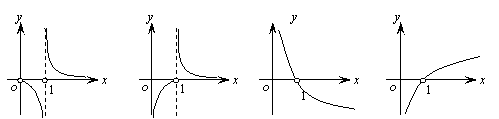 2.函数
2.函数![]() (常数
(常数![]() )的大致图像是
)的大致图像是
A. B. C. D.
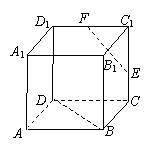 3.如图,正方体ABCD-A1B1C1D1中,E、F分别
3.如图,正方体ABCD-A1B1C1D1中,E、F分别
是CC1、C1D1的中点,则异面直线EF与BD所
成的角的大小为
A.75° B.60°
C.45° D.30°
4.下列命题中正确的是
A.底面是矩形的平行六面体是长方体 ;
B.棱长都相等的直四棱柱是正方体;
C.侧棱垂直于底面两条边的平行六面体是直平行六面体;
D.对角线相等的平行六面体是直平行六面体;
5.两个正数![]() 的等差中项是
的等差中项是![]() ,等比中项是
,等比中项是![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的离
的离
心率![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 的图像按向量
的图像按向量![]() 平移后的图像的一个中心对称点为
平移后的图像的一个中心对称点为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设地球的半径为R,已知赤道上两地A、B间的球面距离为![]() ,若北半球的C地与A、B两地的球面距离均为
,若北半球的C地与A、B两地的球面距离均为![]() ,则C地的纬度为
,则C地的纬度为
A.北纬45° B.北纬60° C.北纬30° D.北纬75°
8.有下列四个命题:
①“直线![]() ”的充分不必要条件是“
”的充分不必要条件是“![]() 垂直于
垂直于![]() 在平面
在平面![]() 内的射影”.
内的射影”.
②“![]() ∥
∥![]() 且
且![]() ∥
∥![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
③“直线![]() 平面
平面![]() ”的充要条件是“直线
”的充要条件是“直线![]() 平面
平面![]() 内的无数条直线”.
内的无数条直线”.
④“平面![]() 的斜线段
的斜线段![]() 在
在![]() 的射影
的射影![]() 与
与![]() 相等”是“
相等”是“![]() ”的充要条件.
”的充要条件.
其中正确命题的个数是
A.3 B.2 C.1 D.0
9.已知为O原点,点![]() 在单位圆
在单位圆![]() 上,点
上,点![]() 满足
满足
![]() ,则
,则![]()
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10.已知平面![]() ∥平面
∥平面![]() ,直线
,直线![]() ,且
,且![]() ,平面
,平面![]() 、平面
、平面![]() 间的距离为5,则在
间的距离为5,则在![]() 内到点
内到点![]() 的距离为13且到直线
的距离为13且到直线![]() 的距离为
的距离为![]() 的点的轨迹是
的点的轨迹是
A.四个点 B.两条直线 C.双曲线的一支 D.一个圆
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共6小题,每小题4分,共24分.把答案填写在答题卡相应位置上.
11.若球的体积是![]() ,则其表面积为
,则其表面积为
12.点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,且在不等式
,且在不等式![]() 表示的平面
表示的平面
区域内,则点![]() 的坐标是___________
的坐标是___________
13.等比数列![]() 中,
中,![]() ,则
,则![]()
14.若![]() ,则圆锥曲线
,则圆锥曲线![]() 的焦点坐标为
的焦点坐标为
15.若二面角![]() 的平面角大小为
的平面角大小为![]() ,直线
,直线![]() ⊥
⊥![]() ,则平面
,则平面![]() 内的直线与
内的直线与![]() 所成角的取值范围是
所成角的取值范围是
16.ABCD-A1B1C1D1是单位正方体,黑、白两只蚂蚁从点A出发沿棱向前爬行,每爬完一
条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1→…,黑蚂蚁爬行的路线是AB
→BB1→…,它们都遵循如下规律:所爬行的第![]() 段与第
段与第![]() 段所在直线必须是异面直
段所在直线必须是异面直
线(其中![]() 是自然数).设黑、白蚂蚁都爬完
是自然数).设黑、白蚂蚁都爬完![]() 段后各自停止在正方体的某个顶点处,
段后各自停止在正方体的某个顶点处,
此时黑、白蚂蚁的距离是
 三、解答题:本大题共6小题,共76分.解答应写出文字说明、证明过程或演算步骤.
三、解答题:本大题共6小题,共76分.解答应写出文字说明、证明过程或演算步骤.
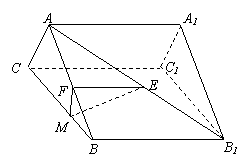
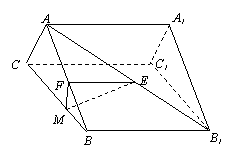
17.(12分)如图,正三棱柱![]() 中
中
点![]() 、
、 ![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)若![]() ⊥
⊥![]() 于点
于点![]() ,求证:
,求证:![]() ⊥
⊥![]() .
.
18.(12分)![]() 且
且![]() 时,解关于x的不等式
时,解关于x的不等式![]() .
.
 19.(13分)海岛上有一座海拔1000米的山,山顶上设有
19.(13分)海岛上有一座海拔1000米的山,山顶上设有
一个灯塔A,上午11时,灯塔A处的值班员测得一匀
速行驶的轮船在岛北偏东60°的C处,由A观察C的
俯角为30°,11时10分又测得该船在岛北偏西60°
的B处,由A观察B的俯角为60°.
(1)求该船的速度 (单位:千米/小时) ;
(2)轮船在沿航线CB航行中,船上的瞭望员随时观测
灯塔发出的导航信号,试问瞭望员在整个观测过程中,观测仰角最大是多少?
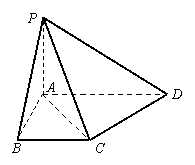 20.(13分)如图,在四棱锥
20.(13分)如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 与底面
与底面![]() 成
成![]() 角.
角.
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求二面角![]() 的平面角的大小;
的平面角的大小;
| |
21.(13分)已知△![]() 的面积为
的面积为![]() ,且
,且![]() ,
,
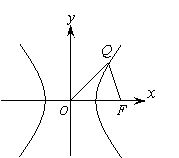 (1)设
(1)设![]() ,求向量
,求向量![]() 与
与![]() 夹角
夹角![]() 的取值范围;
(2)设以
的取值范围;
(2)设以![]() 为中心,
为中心,![]() 为焦点的双曲线经过点
为焦点的双曲线经过点![]() (如图),若
(如图),若
![]() ,
,![]() ,当
,当![]() 取最小值时,求此
取最小值时,求此
双曲线的方程.
22.(13分)设函数![]() 定义域为
定义域为![]() ,当
,当![]() 时,
时,![]() ,且对于任意的
,且对于任意的![]() ,有
,有![]() 成立.数列
成立.数列![]() 满足
满足![]() ,且
,且 ![]() .
.
(1) 求![]() 的值;
的值;
(2) 求数列![]() 的通项公式;
的通项公式;
(3) 是否存在正数![]() ,使
,使![]() 对一切
对一切![]() 均成
均成
立,若存在,求出![]() 的最大值,并证明,否则说明理由.
的最大值,并证明,否则说明理由.
重庆南开中学高2006级2月月考(理科)参考解答
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | A | B | D | C | B | A | D | A | A |
 11、
11、![]() 12、
12、![]() 13、
13、![]() 14、
14、![]() 15、
15、![]() 16、
16、![]()
17、证明:(1)∵E、F分别是正三棱柱中AB1和AB的中点,
∴BB1∥FE 又BB1![]() 平面EFM,FE
平面EFM,FE![]() 平面EFM,
平面EFM,
∴BB1∥平面EFM
(2)∵正三棱柱的侧棱BB1⊥平面ABC,
∴BB1⊥BC
∵BB1∥FE ∴BC⊥FE
又∵MF⊥BC ∴BC⊥平面EFM
∴BC⊥ME
18、解:由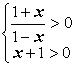 解得
解得![]()
①当![]() 时,原不等式等价于
时,原不等式等价于![]() 即有
即有![]() 解之得
解之得![]() ;
;
②当![]() 时,原不等式等价于
时,原不等式等价于![]() 即有
即有![]() 解之得
解之得![]() ;
;
综上所述:①当![]() 时,解集为
时,解集为![]() ;②当
;②当![]() 时,解集为
时,解集为![]() .
.
19、解:(1)A在海平面上的射影为O,由题意得![]() (千米)
(千米)
![]() (千米),又△
(千米),又△![]() 中∠
中∠![]()
由余弦定理可得![]() (千米),所以该船速度为
(千米),所以该船速度为![]() 船=
船=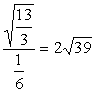 (千米/小时)
(千米/小时)
(2)设点E是CB上的一点,则由AO⊥面BOC得∠AEO即为瞭望员观测灯塔A的仰角,
在Rt△AOE中![]() ,欲使∠AEO取最大值,则OE应取最小值.
,欲使∠AEO取最大值,则OE应取最小值.
当OE⊥CB时,OE可取最小值.
由![]() 可得
可得![]()
∴![]() ∴瞭望员观测灯塔A的仰角最大为
∴瞭望员观测灯塔A的仰角最大为![]() .
.
20、解:(1)法一:∵PA⊥面ABCD 且AB⊥BC,AB是PB面ABCD内的射影
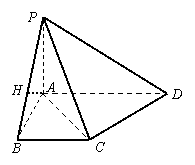 ∴PB⊥BC (三垂线定理)
∴PB⊥BC (三垂线定理)
∴PB⊥面PAB 且BC![]() 面PBC
面PBC
∴面PBC⊥面PAB 其交线为PB
过A在平面PAB内作AH⊥PB于H,则AH⊥面PBC
∴AH即为点A到平面PBC的距离
又∵PA⊥面ABCD
∴AD是PD在面ABCD内的射影
∴∠PDA即为PD与面ABCD所成的角,即∠PDA=30°
∵AD=3 ∴PA=![]() PB=2 AB=1 ∴AH=
PB=2 AB=1 ∴AH=![]()
法二:(等积法)设点A到平面PBC的距离为![]() ∵PA⊥面ABCD ∴
∵PA⊥面ABCD ∴![]() P-ABC =
P-ABC =![]() A-PBC
A-PBC
即![]() ∵AB=BC=1且∠ABC=90°∴
∵AB=BC=1且∠ABC=90°∴![]()
解得![]()
(2)∵PA⊥面ABCD 且PA![]() 面PAC ∴面PAC⊥面ABCD 其交线为AC
面PAC ∴面PAC⊥面ABCD 其交线为AC
过点B在平面ABCD内作BM⊥AC于M,则BM⊥面PAC
又过点M在平面PAC内作MN⊥PC于N,
连结MN,则BN⊥PC (三垂线定理)
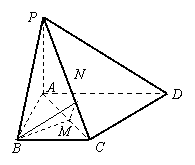 ∴∠BNM即为二面角
∴∠BNM即为二面角![]() 的平面角
的平面角
在Rt△PBC中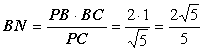
在Rt△ABC中![]()
∴在Rt△BMN中![]()
即二面角![]() 的平面角的大小为
的平面角的大小为![]() (
(![]() 、
、![]() )
)
21、解:(1)由已知,得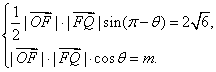
∴![]() ∴
∴![]() ,则
,则![]() (2)设所求的双曲线方程为
(2)设所求的双曲线方程为![]() =1 (a>0,b>0),点Q(x1,y1),则
=1 (a>0,b>0),点Q(x1,y1),则![]() =(x1-c,y1)
=(x1-c,y1)
∵△OFQ的面积![]()
![]() y1=2
y1=2![]() ∴y1=±
∴y1=±![]()
又由![]() ·
·![]() =(c,0)
(x1-c,y1)=(x1-c)c=(
=(c,0)
(x1-c,y1)=(x1-c)c=(![]() -1)c2 ∴x1=
-1)c2 ∴x1=![]() c
c
![]() =
=![]() ≥
≥![]() ,当且仅当c=4时,
,当且仅当c=4时,![]() 最小.
最小.
此时Q的坐标为(![]() ,
,![]() ),或(
),或(![]() ,-
,-![]() ).由此可得
).由此可得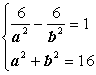
解得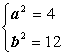 故所求方程为
故所求方程为![]() =1.
=1.
22、解:(1)令![]() ,得
,得![]() ,得
,得![]()
(2)当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
设![]() ,且
,且![]() ,
,
![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,而
,而![]() ,
,
∴![]() ,即
,即![]() .∴函数
.∴函数![]() 在
在![]() 上是减函数.
上是减函数.
由![]() 得
得![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]()
![]() .
.
∴![]() 是等差数列,其首项为1,公差为
是等差数列,其首项为1,公差为![]() ,∴
,∴![]()
(3)存在正数![]() ,使
,使![]() 成立.
成立.
记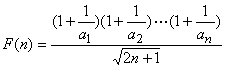 ,则
,则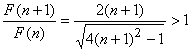 ,
,
∴![]() 单调递增,∴
单调递增,∴![]() 为
为![]() 的最小值,由
的最小值,由![]()
![]() 恒成立知
恒成立知![]() ,
,
∴![]() 的最大值为
的最大值为![]() .
.