舟山中学高三数学月考试卷(理科)2006、3
一、选择题：(本大题共10小题，每题5分，共50分，正确答案唯一)
1、由下列各组命题构成的“
或
”， “且”，“非”形式的复合命题中，“或”为真， “且”为假，“非”为真的是
( )
A、：3是偶数，：4是奇数
B、：3+2=6，,5>3
C、：
：
D、：
，：
2、ABCD为正方形，PD⊥平面ABCD，则二面角A－PB－C的大小范围是 ( )
A、
B、
C、
D、
3、在等差数列
中
，则此数列前13项的和为( )
A、 156 B、13 C、12 D、26
4、设
(0，л/2)，且
则
=( )
A、л/6 B、-л/3 C、л/3 D、-л/3或л/3
5、若函数
对任意的实数x都有
成立，则直线
的倾斜角为
( )
A、arctan2 B、arctan(-2) C、
D、
6、函数
在区间［0,1］上是
( )
A、单调递增的函数 B、单调递减的函数 C、先减后增的函数 D、先增后减的函数
7、某校有6间不同的电脑室，每天晚上至少开放2间，欲求一天中不同安排方案的种数，现有四位同学分别给出下列四个结果：①
；②
；③
；
④
。其中正确的结论是
( )
A、仅有① B、 ②和 ④ C、②和③ D、仅有③
8、已知双曲线
和椭圆
离心率互为倒数，那么以
、b、m为边的三角形一定是
( )
A、直角三角形 B、等腰三角形 C、锐角三角形 D、钝角三角形
9、由等式
定义
，则
为
( )
A、(1，2，3，4) B、(0，3，4，0) C、(-1，0，2，-2) D、(0，-3, 4，-1)
10. 已知函数
满足：①
；②在
上为增函数。( )
若
,且
,则
与
的大小关系是
A、
B、
C、
D、 无法确定
二、填空题：(本大题共4小题，每题4分，共16分)
11、现有15名新生，其中有3名优秀生，将他们随机地分到三个班级中去，每班5人，则每班都分到优秀生的概率是_____________。
12、已知
是可导的偶函数，且
，则曲线
在(-1,2)处的切线方程是________________________________________。
13、已知
, 则
的值为
__。
14、定义： 
×
=··sinθ，其中θ为向量与的夹角，若=2, =5, ·=-6,则×=______________________。
三、解答题：（本大题共6小题，共84分.解答应写出文字说明，证明过程或演算步骤.）
15、(本题满分14分) 本题共有3小题,第1小题满分6分, 第2小题满分5分.第3小题3分)。已知函数f(x)=2sin(x+
)-2cosx,x∈[
,
].
(1) 若sinx=
,求函数f(x)的值;(2)求函数f(x)的值域.
(3)若
，指出可由
经过怎样的变换得到。
|
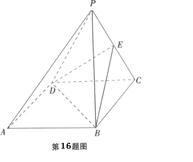
（1）求证：PA//平面EDB；
（2）求证：平面EDB⊥平面PBC；
（3）求二面角D-PB-C的正切值。
17、（本小题满分14分）某次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题， 并且宣布：观众答对问题A可获奖金a元，答对问题B可获奖金2a元；先答哪个题由观众自由选择；只有第1个问题答对，才能再答第2个问题，否则中止答题。若你被选为幸运观众，且假设你答对问题A、B的概率分别为
、
。你觉得应先回答哪个问题才能使你获得奖金的期望较大？说明理由。
18、(本题满分14分)已知当时，不等式
恒成立，求实数的取值范围。
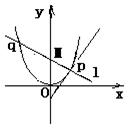
19、(本题满分14分)如图：P是抛物线C
上一点，直线
过点P并与抛物线C在点
P的切线垂直，与抛物线C相交于另一点Q。
(1) 当点P的横坐标为2 时，求直线的方程；
(2) 当点P在抛物线上移动时，求线段PQ中点M的轨迹方程，并求点M到
轴的最短距离。
|
20、 (本题满分14分) 已知数列al，a2…，a30，其中al，a2…，a10是首项为1公差为1的等差数列；al0，a11…，a20是公差为d的等差数列；a20，a21…，a30是公差为d2的等差数列
(d≠0).(1)若a20=40，求 d；
(2)试写出a30关于d的关系式，并求a30的取值范围;
(3)续写己知数列，使得a30，a31…，a40是公差为d3的等差数列，……，依次类推，把已知数列推广为无穷数列．提出同(2)类似的问题,((2)应当作为特例),并进行研究，你能得到什么样的结论？
舟山中学高三数学月考(理)参考答案：
一、选择题