绝密★启用前
宿迁市2004—2005学年度高三年级第三次考试
数 学 05.5
注意事项：
1、答卷前，考生务必将自己的姓名、准考证号准确地写在答题卡上。
2、所有试题的答案均写在答题卡上。对于选择题，每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案。
3、考试结束后，将本试卷和答题卡一并交回。
参考公式：
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么
P(A·B)=P(A)·P(B) 其中R表示球的半径
如果事件A在一次试验中发生的概率是 球的体积公式
p，那么n次独立重复试验中恰好发生k
次的概率
其中R表示球的半径
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．若双曲线的实半轴长为2，焦距为6，则该双曲线的离心率为
（A）
（B） 
（C） 
（D） 3
2．函数f (x) =sin2x， x∈[－π，π]，则满足f (x)=0的x有
（A）2个 （B）3个 （C）4个 （D）5个
3．函数
和
，
，
，则它们的反函数的图象关于
（A）x轴对称 （B）y轴对称 （C）关于直线y=x对称 （D）原点对称
4．给出关于平面向量的两个命题：
①
是非零向量，且
=
，则
=
；
②，是非零向量，⊥，则+=－。正确的命题的序号是
（A）① （B）② （C）①② （D）没有正确的命题
5．设a、b表示直线，α、β表示平面，α//β的充分条件是
（A）a
α，bβ，a//b
（B）aα，bβ，a//β，b//α
（C）a⊥b，α⊥β，b⊥α （D）a//b, a⊥α，b⊥β
6．设等差数列{an}前n项和为Sn，则使S6=S7的一组值是
（A）a3=9， a10=―9 （B）a3=―9，a10= 9
（C）a3=―12， a10=9 （D）a3=―9，a10=12
7．函数
在
上是单调减函数，则a的最大值是
（A）―3 （B）―1 （C）1 （D）3
8．设二项式（3x+1）n的展开式的各项系数和为an，展开式中x2的系数为bn。若an+bn=310，则n等于（ ）
（A）3 （B）4 （C）5 （D）6
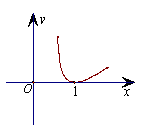
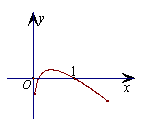
9．函数
的图象大致形状是
（A） （B） （C） （D）
10．对某种产品的4件不同正品和4件不同次品一一进行检测，直到区分出所有次品为止。若所有次品恰好经过五次检测被全部发现，则这样的检测方法有
（A）96种 （B） 120种 （C）384种 （D）480种
11．把函数f (x)=2sin(
)cos(
)的图象向左平移a（a>0）个单位，得到函数y=g (x)的图象。若函数y= g (x)是奇函数，则a的最小值为
（A） 
（B） 
（C） 
（D）
12．经济学中的“蛛网理论”（如图），假定某种商品的“需求—价格”函数的图象为直线l1,“供给—价格”函数的图象为直线l2，它们的斜率分别为k1、k2，l1与l2的交点P为“供给—需求”均衡点，在供求两种力量的相互作用下，该商品的价格和产销量，沿平行于坐标轴的“蛛网”路径，箭头所指方向发展变化，最终能否达于均衡点P，与直线l1、 l2的斜率满足的条件有关，从下列三个图中可知最终能达于均衡点P的条件为
 |
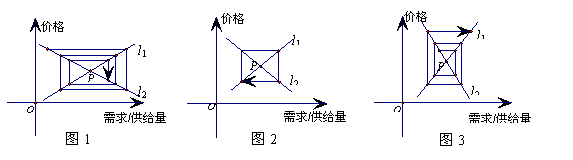（A）k1+k2>0 （B）k1+k2=0 （C）k1+k2<0 （D）k1+k2可取任意实数
二、填空题（本大题4个小题，每小题4分，共16分，只填结果，不要过程）
（13）在下图中，直线L为曲线C在点P处的切线，则直线L的斜率是
 |
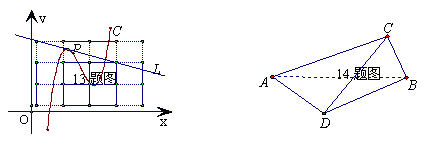（14）如图，直角三角形ABC中，
，△ABD为等腰直角三角形，
。当点D到平面ABC距离最大时，直线CD与平面ABC所成角为___________
（15）平面内满足不等式组（x+y—4）（x+ 2y—6）≤0，x≥0，y≥0的所有点中，使目标函数z=5x+4y取得最大值的点的坐标是
（16）已知O为原点，点P (x、y)在单位圆x2 + y2 = 1上，点Q (2cosθ, 2sinθ)满足
=（
），则
= ___________
.三、解答题：本大题6个小题，共74分.解答必需写出必要的文字说明、推理过程或计算步骤.
(17) 解不等式
(18) 某公交公司对某线路客源情况统计显示，公交车从每个停靠点出发后，乘客人数及频率如下表：
| 人数 | 0~6 | 7~12 | 13~18 | 19~24 | 25~30 | 31人以上 |
| 频率 | 0.1 | 0.15 | 0.25 | 0.20 | 0.20 | 0.1 |
（I）从每个停靠点出发后，乘客人数不超过24人的概率约是多少？
（II）全线途经10个停靠点，若有2个以上（含2个），乘客人数超过18人的概率大于0.9，公交公司就要考虑在该线路增加一个班次，请问该线路需要增加班次吗？
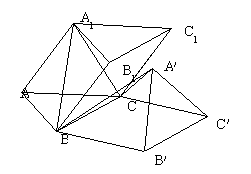
(19) 在三棱柱
中，底面
为正三角形，
，
。
（I）求证：
；
（II）把四棱锥
绕直线
旋转到
，使平面与平面
重合，试求旋转过的角的余弦值。
(20) 已知锐角α，β满足2sinβ=sin（2α+β）且α+β≠.
（I）求证：tan(α+β)=3tanα
（II）设y=tanβ, x=tanα, α∈[，]试求函数y=f (x)的最大值
(21) 设Sn为数列{an}的前n项和，如果Sn=2an－3n+5.
（I）证明：数列{an+3}是等比数列；
（II）是否存在正整数p、q、r（p<q<r）使得p,q, r和Sp，Sq，Sr同时成等差数列？若存在，求出p、q、r的值，若不存在，请说明理由。
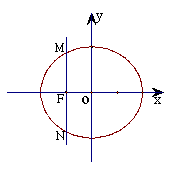
(22) （Ⅰ）椭圆
的左焦点为F，过F作垂直于x轴的直线与椭圆交于点M、N，相应的准线与x轴交于点H，求证：∠MHN为锐角,且直线MH与椭圆有且仅有一个公共点。
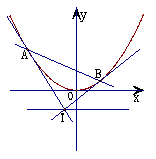
（Ⅱ）请针对抛物线y=
，类比（I），写出一个真命题（不要求给出证明过程）。
（Ⅲ）动直线l与（Ⅱ）中抛物线交于不同的两点A、B，满足
=m
（m∈R）,抛物线在点A处的切线为l1，在点B处切线l2，切线l1与l2交点为T，求证：点T在准线上。
绝密★启用前
宿迁市2004—2005学年度高三年级第三次考试
数学试题参考答案及评分标准
说明：
一、本解答给出了一种或几种解法供参考，如果考生的解答与本解答不同，可根据试题的主要考查内容参照评分标准制定相应的评分细则。
二、对解答题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不在给分。
三、解答右端所注的分数，表示考生正确做到这一步应得的累加分数。
四、只给整数分数，选择题和填空题不给中间分数。
一、选择题（每小题5分，满分60分）
1、D 2、C 3、B 4、B 5、D 6、 C
7、A 8、B 9、A 10、C 11、C 12、A
二、填空题（每小题4分，满分16分）
13、 ； 14、 ； 15、（6，0）； 16、 
.
三、解答题
17（本题满分12分）
解：原不等式可化为
……………………………………………4分
∵x+1>0恒成立 ∴（x－2）（x－1）<0 …………………………5分
∴1<x<2 ……………………………………………………………8分
∴－2<x<－1或1<x<2 …………………………………………11分
∴原不等式的解集为{x－2<x<－1或1<x<2} ……………………… 12分
（18）（本题满分12分）
解：（Ⅰ）每个停靠点出发后，乘客人数不超过24人的概率约为
0.1+0.15+0.25+0.2=0.7 …………………………………………………4分
(Ⅱ)从每个停靠点出发后，乘客人数超过18人的概率为
0.20+0.20+0.1=0.5 ……………………………………………………… 6分
途经10个停靠点，没有一个停靠点出发后，乘客人数超过18人的概率为
……………………………………………………7分
途经 10个停靠点，只有一个停靠点出发后，乘客人数超过18人的概率
………………………………………9分
所以，途经10个停靠点，有2个以上（含2个）停靠点出发后，乘客人数超过18人的概率
P=1－－C
（
）（1－）9=1－
=
…………11分
∴该线路需要增加班次。
答：（Ⅰ）每个停靠点出发后，乘客人数不超过24人的概率约为0.7
(Ⅱ) 该线路需要增加班次 ………………………………………………12分
（19）（本题满分12分）
解：（Ⅰ）∵A1C1∥AC，∠BA1C1=90°
∴A1B⊥AC……………………………………………………………………2分
同理A1C⊥AB
过A1作A1H⊥底面ABC，H为垂足，连接CH、BH、AH
由三垂线定理的逆定理 BH⊥AC，CH⊥AB…………………………………………4分
∴H为△ABC的垂心
∴AH⊥BC
由三垂线定理 AA1⊥BC…………………………………………………………………6分
(Ⅱ) 即求二面角B1―BC―B′大小的余弦值
∵AA1∥BB1，由（Ⅰ）知B B1⊥BC，从而BB′⊥BC
∴∠B1BB′为二面角B1―BC―B′的平面角……………………………………………9分
且有BB′∥AH（在底面内AH、BB′同垂直于BC）
∴∠B1BB′=∠A1AH（∠B1BB′与∠A1AH的两边分别平行，且方向相同）
∵△ABC为正三角形
∴H为△ABC的中心
∵
在Rt△A1AH中，cos∠A1AH=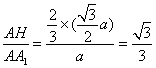
∴cos∠B1BB′=
………………………………………………………………………12分
（20）（本题满分12分）
解：（Ⅰ）由条件有2sin[(α+β)－α]=sin[(α+β)+ α]
由两角和差的正弦公式有
2sin(α+β)cosα－2cos(α+β)sinα=sin(α+β)cosα+ cos(α+β)sinα
整理得：sin(α+β)cosα=3 cos(α+β)sinα…………………………………………3分
∵α、β为锐角，且α+β≠
∴cosα·cos(α+β)≠0
两边同除以cosα·cos(α+β)得 tan(α+β)=3tanα…………………………………6分
（II）tanβ=tan[(α+β) －α]= 
=
=
∴ y=
∵α∈[
] ∴x=tanα∈[1，+∞] ……………………………………………9分
假设x1，x2∈[1，+∞)，且x1<x2.
f (x1)－f (x2)= 
－
=
∵1≤x1<x2<+∞
∴x2－x1>0且3x1x2－1>0
又（1+3x
）(1+3x
)>0
∴f(x1)－f(x2)= 
∴f (x1)>f(x2)
∴ f (x)在[1，+∞）上是减函数
∴当x=1时，f (x)达到最大值f (1)= 
.………………………………………12分
（21）（本题满分12分）
解：（I）由条件
an+1=Sn+1－Sn=[2an+1－3(n+1)+5]－(2an－3n+5)=2an+1－2an－3…………………………3分
∴an+1=2an+3
∴an+1+3=2(an+3)
∴{an+3}是等比数列…………………………………………………………………6分
（II）注意到a1=S1，在条件中取 n=1,得 a1=－2
∴an+3=(a1+3) ×2n－1=2n－1 ∴an=2n－1－3
代入条件得Sn=2n－3n+1……………………………………………………………8分
假设满足条件的正整数p、q、r存在
则
┈①
┈②
由②得（2p－3p+1）+(2r－3r+1)=2(2q－3q+1)
即2p+2r－3(p+r)=2×2q－6q
将①代入得2p+2r=2q+1……………………………………………………………………10分
假设等差数列p 、q、r公差为d，则q=p+d, r=p+2d， d∈N*
∴代入上式有2p+2p+2d=2p+d+1
两边同除以2p ，得1+22d=2d
即(2d－1)2=0，∴2d=1
∴d=0，与d∈N*矛盾
∴满足条件的p、q、r不存在. …………………………………………………………12分
（22）（本题满分14分）
解： （I）a=2, b=
， c=1，左焦点F (－1, 0)，左准线方程x=－4
∴H（－4，0）………………………………………………………1分
将x=－1代入，得M(－1，)，N（－1，－）………………………2分
KMH=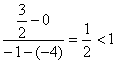
∴∠MHF<
由对称性可知∠MHN< ………………………………………………………………3分
直线MH方程为y=(x+4)，即y=x+2
代入，消去y并整理得 x2+2x+1=0
该方程得判别式△=0
∴直线MH与椭圆只有一个公共点，即为点M……………………………………5分
（II）
| 若抛物线y= 则∠MHN为直角,且直线MH与抛物线有且仅有一个公共点. |
的焦点为F，过F作垂直于y轴的直线与抛物线交于点M、N，准线与y轴交于点H，……………………………………………7分
（Ⅲ）法一：即证T点纵坐标y=－
由
……………………………………………………8分
设A（2pt1, 2pt），B（2pt2, 2pt）, (t1≠t2), 直线l1、l2的斜率分别为k1、k2
，
=(2pt2 ,2pt－)
∴2pt1(2pt－)－2pt2(2pt
)=0，即2p2(t1－t2)(4t1t2+1)=0
∵p>0, t1≠t2 ∴4t1t2+1=0
， 即t1t2=－
┈①………………………………10分
记f(x)= 
,则f′(x)
=()′=
∴k1= f′(2pt1) =2t1……………………………………………………11分
直线l1的方程为 y－2pt=2t1(x－2pt1)
即y=2t1x－2pt┈②
同理l2：y=2t2x－2pt┈③……………………………………………………………12分
②×t2－③×t1并将①代入消去x得：（t2－t1）y=（t1－t2）
∵t1≠t2 ∴y=－
∴点T在准线上。……………………………………………………………………14分
法二：∵
∴直线l过点F（0，）………………………8分
假设直线l的斜率为k，点A、B坐标分别为（x1, y1）, (x2, y2)（x1≠x2）
则l的方程为y=kx+，代入y=
消去y并整理得 x2－2px－p2=0
由韦达定理 x1x2=－p2┈①
又y1=
, y2=
∴x1y2－x2y1=
┈②……10分
记f(x)= 
，则f′(x) =()′=
∴k1= f′(x1)
=
……………………………………………………………11分
l1方程为y－y1=
┈③
同理，l2方程为y－y2=
┈④……………………………………………………………12分
③×y2－④×y1，并将①、②代入消去x得
（x2－x1）y－(x2－x1)= －p (x2－x1)
∵x1≠x2 ∴y=－
∴点T在准线上……………………………………………………………………………14分