 望城县第一中学2006届高三第三次月考理科数学试卷
望城县第一中学2006届高三第三次月考理科数学试卷
命题:陈国军 时量:120分钟 总分150分(第2卷)答题卷(理)
一、单项选择题:(5分×10=50分) 总分_______
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题:(4分×5=20分)
11.____________, 12._____________, 13.____________;14____________,15.________________
三、解答题:(共6小题满分80分)
16 、(14分)已知M(2![]() , 1), N (1,
, 1), N (1, ![]() +a) (x,a∈R, a是常数),
+a) (x,a∈R, a是常数),
且 y = ![]()
![]()
![]() (O是坐标原点).
(O是坐标原点).
①求y关于x的函数关系式 y = f ( x ) ,
②若x∈[![]() ,
,![]() ]时,f ( x
) 的最小值为2,求a的值,并求f(x)的最小正周期.
]时,f ( x
) 的最小值为2,求a的值,并求f(x)的最小正周期.
③在②下说明f (x)(![]() )的图像可由y=2sin2x(
)的图像可由y=2sin2x(![]() )的图像经过怎样的变换而得到。
)的图像经过怎样的变换而得到。
17.( 12分)设数列{an}的前n项和为Sn,若对于任意的n∈N*,都有Sn=2an-3n .
⑴求数列{an}的首项a1与递推关系式:an+1=f(an);
⑵先阅读下面定理:“若数列{an}有递推关系an+1=Aan+B,其中A、B为常数,且A≠1,B≠0,则数列![]() 是以A为公比的等比数列。”请你在⑴的基础上应用本定理,求数列{an}的通项公式;
是以A为公比的等比数列。”请你在⑴的基础上应用本定理,求数列{an}的通项公式;
⑶求数列{an}的前n项和Sn .
18.( 12分)己知向量![]() =(
=(![]() ),
),![]() =(
=(![]() ),
),![]() =(3,0).①若
=(3,0).①若![]() ,且
,且![]() 都为锐角,求
都为锐角,求![]() 的值.
的值.
②若![]() ,且
,且![]() 求
求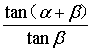 的值.
的值.
。
19,(14分)某工厂有容量为300吨的水塔一个,每天从早上6时起到晚上10时止供应该厂生活和生产用水。已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间![]() (单位:小时,定义早上6时
(单位:小时,定义早上6时![]() =0)的函数关系式为
=0)的函数关系式为![]() ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,每小时的进水量增加10吨,若某天水塔原有水100吨,在供水同时打开进水管。
,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,每小时的进水量增加10吨,若某天水塔原有水100吨,在供水同时打开进水管。
(1)设进水量选用第![]() 级,写出在
级,写出在![]() 时刻水的存有量;
时刻水的存有量;
(2)问进水量选择第几级,既能保证该厂用水(水塔中水不空)又不会使水溢出。
(注:存有量=进水量-用水量+原有量,用水量=生活用水量+工业用水量。)
20. (14分)己知函数![]()
① 若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和,求g(x)和h(x)的解析式.
② 命题P:函数f(x)在区间![]() 上是增函数;命题Q:函数g(x)是减函数.如果命题P、Q有且仅有一个是真命题,求
上是增函数;命题Q:函数g(x)是减函数.如果命题P、Q有且仅有一个是真命题,求![]() 的取值范围.
的取值范围.
③ 在②的条件下,比较f(2)与3-lg2的大小.

21(14分)设点集![]() ,点
,点![]() 在
在
L中,p1 为L与y轴的交点,数列![]() 的前n项和Sn=n2 .
的前n项和Sn=n2 .
⑴求数列![]() 的通项公式.
的通项公式.
⑵若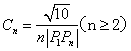 ,计算
,计算![]()
![]() .
.
⑶ 设函数![]() ,足否存在
,足否存在 ![]() ,使得f(k+10)=3f(k),
,使得f(k+10)=3f(k),
若存在,求出k的值;若不存在,说明理由.
望城县第一中学2006届高三第三次月考数学试卷
命题:陈国军 时量:120分钟 总分150分(第1卷)客观题(理)
一、单项选择题:(5分×10=50分)(以下各题仅有一个答案符合题目要求,请选出其代号填入第2卷相应的答题卡内,多选、少选记0分)
1.己知集合![]() ,则关于
,则关于![]() 的以下说法正确的是( )
的以下说法正确的是( )
A. ![]() 中只有一个元素;B.
中只有一个元素;B. ![]()
![]() ;C.
;C. ![]() =A;D.
=A;D. ![]() =
=![]() .
.
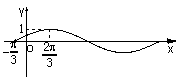 2.若函数
2.若函数![]() 的图象(部分)如图所示,则
的图象(部分)如图所示,则![]() 的取值是( )
的取值是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.己知![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设等差数列{an}的前n项的和为Sn,若a1>0,S4=![]() ,则当Sn取得最大值时,n的值为 ( )
,则当Sn取得最大值时,n的值为 ( )
A.5 B.6 C.7 D.8
5.函数f(x)=sin![]() x+cos(
x+cos(![]() x+1)的图象相邻的两条对称轴间的距离是( )
x+1)的图象相邻的两条对称轴间的距离是( )
A.3π B.![]() C.
C.![]() D.
D.![]()
6. 函数![]() 的最大值为( )
的最大值为( )
A.0
B. ![]() C.
C.![]() D.
D. ![]()
7.若偶函数f(x)在区间[-1,0]上是减函数,![]() 、
、![]() 是锐角三角形的两个内角,且
是锐角三角形的两个内角,且![]() ≠
≠![]() ,则下列不等式中正确的是(
)
,则下列不等式中正确的是(
)
A.f(cos![]() )>f(cos
)>f(cos![]() ) B.f(sin
) B.f(sin![]() )>f(cos
)>f(cos![]() ) C.f(sin
) C.f(sin![]() )>f(sin
)>f(sin![]() ) D.f(cos
) D.f(cos![]() )>f(sin
)>f(sin![]() )
)
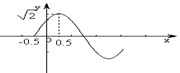 8. 若函数
8. 若函数![]() 的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2005)+f(2006)等于( )
的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2005)+f(2006)等于( )
A.0; B.1; C.2; D.-1
![]() 则函数f(x)=
则函数f(x)=![]() ( )
( )
A.是偶函数不是奇函数; B. 是奇函数不是偶函数;
C. 既是偶函数又是奇函数; D. 既不是偶函数又不是奇函数;
10.己知f(x)=xsinx,若x1,x2![]() ,且f(x1)>f(x2),则下列不等式必定成立的是( )
,且f(x1)>f(x2),则下列不等式必定成立的是( )
A.x1>x2
B. x1<x2,
C.![]() D.
D.![]()
二、填空题:(4分×5=20分)
11.已知![]() 为第二象限角,且cos
为第二象限角,且cos![]() ,则cot
,则cot![]() 的值是__________.
的值是__________.
12.设A、G分别是sinx与cosx的等差中项与等比中项,则A+G2的最大值为____________.
13.已知![]() ,把数列
,把数列![]() 的各项排成三角形状;
的各项排成三角形状;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
……
记A(m,n)表示第m行,第n列的项,则A(10,8)= .
14.给定![]()
则区间[1,2005]内所有希望数之和为_________________
15.已知函数![]() 互为反函数,又
互为反函数,又![]() 的图象关于直线
的图象关于直线![]() 对称,若
对称,若![]() ___
__;
___
__;
![]() _______
.
_______
.