漳平二中2005-2006学年第二学期
高三数学单元考试测试卷（文科）
NO.5 直线与圆锥曲线
（时间：120分钟 满分：150分）
班 姓名 座号
一、选择题（共16题，每题有且只有一个答案正确。每小题5分，共80分）
1．以A（1，3）、B（－5，1）为端点的线段的垂直平分线的方程是 （ ）
A．
B．
C．
D．
2．函数
的一条对称轴方程是
,则直线
的倾斜角为 ( )
A．
B．
C．
D．
3．△ABC中，
是内角A、B、C的对边，且
成等差数列，则下列两条直线
的位置关系是：（ ）
A．重合 B．相交（不垂直） C．垂直 D．平行
4．光线由点
射到直线
上，反射后过点
，则反射光线方程为 （ ）
A．
B．
C．
D．
5．圆
上到直线
的距离为
的点共有 （ ）
A．1个 B．2个 C．3个 D．4个
6．已知定直线l外一定点A，过点A且与l相切的圆的圆心轨迹是 （ ）
A．抛物线 B．双曲线 C．椭圆 D．直线
7．双曲线
，过焦点
的弦
长为
，另一焦点为
，则△
的周长为 （ ）
A．
B．
C．
D．
8．椭圆方程为
，令
，那么它的准线方程为 （ ）
A．
B．
C．
D．
9．如果双曲线的实半轴长为2，焦距为6，那么该双曲线的离心率为 （ ）
A．
B．
C．
D．2
10．圆锥曲线
的准线方程是 （ ）
A．
B．
C．
D．
11．如果动圆与圆
外切且与直线相切，那么动圆的圆心的轨迹方程是（ ）
A．
B．
C．
D．
12．设F1、F2为双曲线
的两个焦点，点P在双曲线上满足∠F1PF2=90°，那么△F1PF2的面积是 （ ）
A．1 B．
C．2 D．
13.设双曲线，的一条准线与两条渐近线交于A，B两点，相应焦点为F，若以AB为直径的圆过点F，则双曲线离心率为 ( )
A． B．
C．2 D．
14．已知P为椭圆
在第三象限内一点，且它与两焦点连线互相垂直。若点P到直线
的距离不大于3，则实数的取值范围是 ( )
A．
B．
C．
D．
15．已知椭圆
与双曲线
有相同的焦点
和
.若
是
的等比中项，
是
与
的等差中项，则椭圆的离心率是 ( )
A．
B．
C．
D．
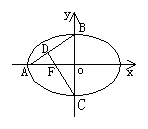16．如图，椭圆中心在原点，离心率为，
为左焦点，直线与
交于点
,则
等于( )
A．
B．
C．
D．
二、填空题（共8题，每小题4分，共32分）
17．直线y=xtg300°+1的倾角为 .
18．点
分有向线段
所成的比
，点P1和点P2在直角坐标系中的坐标分别为P1（0，－6）和P2（3，0），则点的坐标是 .
19．在直角坐标系中，通过点（0，0），（1，0）和（0，2）的圆的方程是 .
20．已知椭圆的两个焦点是F1（0，－1）和F2（0，3），并且点A（2，1）在该椭圆上，那么这个椭圆的方程是 .
21．双曲线
的渐近线方程是
.
22．若双曲线
左支上的一点
到直线
的距离为
，则
.
23．在抛物线
上求一点，使该点到直线
的距离为最短，该点的坐标是 .
24．抛物线
和圆
上最近两点之间的距离是 .
三、解答题：本大题共5小题，共38分。解答应写出文字说明，证明过程或演算步骤。
25．（本题满分6分）在直角坐标系中，过点P（－3，4）的直线l与直线OP的夹角为45°，求直线l的方程.
26．（本题满分6分）求圆心在抛物线
的顶点，并且与抛物线的准线相切的圆的方程.
27．（本题满分8分）
（1）抛物线
截直线
所得的弦长为
，求
的值.
（2）以本题（1）所得到的弦为底边，以x轴上的点P为顶点作三角形，当这个三角形的面积为9时，求点P的坐标.
28．（本题满分9分）设
分别为椭圆：
的左、右两个焦点。
（1）若椭圆C上的点A（1，
）到两点的距离之和等于4，写出椭圆的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段
的中点的轨迹方程.
29．（本题满分9分）双曲线G的中心在原点O，并以抛物线
的顶点为右焦点，以此抛物线的准线为右准线.
（1）求双曲线G的方程；
（2）设直线
与双曲线G相交于A、B两点，
①当k为何值时，原点O在以AB为直径的圆上？
②是否存在这样的实数k，使A、B两点关于直线
为常数）对称？若存在，求出k的值；若不存在，说明理由.