上海市徐汇区2006届高三第一学期期末抽查数学试卷
一、填空题:
1.
函数![]() 的定义域为
的定义域为 ![]() 。
。
2.
已知集合![]() ,则集合
,则集合![]()
![]() 。
。
3.
函数![]() 的最小正周期是
的最小正周期是 ![]() 。
。
4.
设复数![]() ,则
,则![]()
![]() 。
。
5.
函数![]() 的最大值为
的最大值为 ![]() 。
。
6.
方程![]() 的解是
的解是 ![]() 。
。
7.
已知数列![]() 的前
的前![]() 项和
项和![]() ,则
,则![]() 的最小值为
的最小值为 ![]() (结果用数值表示)。
(结果用数值表示)。
8.
将4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有
![]() 种。
种。
9.
已知直线![]() 过点
过点![]() ,当直线
,当直线![]() 与圆
与圆![]() 有两个公共点时,其斜率
有两个公共点时,其斜率![]() 的取值范围是
的取值范围是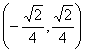 。
。
10、计算: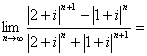
![]() 。(其中
。(其中![]() 为虚数单位)
为虚数单位)
11、设双曲线![]() 的实轴长、虚轴长、焦距成等差数列(公差不为零),则双曲线一个可能的方程为
的实轴长、虚轴长、焦距成等差数列(公差不为零),则双曲线一个可能的方程为
![]() 。
。
12、关于![]() 的方程
的方程![]() 恰有四个不相等的实数根,则实数
恰有四个不相等的实数根,则实数![]() 的取值范围是
的取值范围是 ![]() 。
。
13、若函数![]() 在
在![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是
的取值范围是 ![]() 。
。
14、对任意实数![]() ,定义运算
,定义运算![]() ,其中
,其中![]() 为常数,等号右边的运算是通常意义的加、乘运算。现已知
为常数,等号右边的运算是通常意义的加、乘运算。现已知![]() ,且有一个非零实数
,且有一个非零实数![]() ,使得对任意实数
,使得对任意实数![]() ,都有
,都有![]() ,则
,则![]()
![]() 。
。
二、选择题:
15、函数![]() 的反函数是 ( B )
的反函数是 ( B )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
16、点P从![]() 出发,沿单位圆
出发,沿单位圆![]() 逆时针方向运动
逆时针方向运动![]() 弧长到达Q点,则Q的坐标为 ( A )
弧长到达Q点,则Q的坐标为 ( A )
A、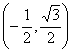 B、
B、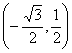 C、
C、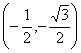 D、
D、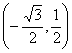
17、![]() 中,若
中,若![]() ,则
,则![]() 为
( C )
为
( C )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
18、已知![]() ,则数列
,则数列![]() 的通项公式
的通项公式![]() 等于
( D )
等于
( D )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、解答题
19、解不等式组: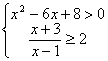
解: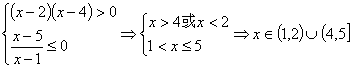 。
。
20、已知数列![]() 的首项是
的首项是![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式。
的通项公式。
解:![]() ,两式相减,得
,两式相减,得![]() ,
,
∴![]() 。
。
21、已知函数![]()
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)求函数![]() 在
在![]() 上的值域。
上的值域。
解:(1)![]()
![]()
∴函数![]() 的最小正周期
的最小正周期![]() 。
。
(2)∵![]()
![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 。
。
22、某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为![]() ,贷款的利率为6%,又银行吸收的存款能全部放贷出去。
,贷款的利率为6%,又银行吸收的存款能全部放贷出去。
(1)若存款的利率为![]() ,试分别写出存款数量
,试分别写出存款数量![]() 及银行应支付给储户的利息
及银行应支付给储户的利息![]() 与存款利率
与存款利率![]() 之间的关系式;
之间的关系式;
(2)存款利率定为多少时,银行可获得最大收益?
解:(1)存款量![]()
![]() ,银行应支付的利息
,银行应支付的利息![]()
![]() 。
。
(2)设银行可获得收益为![]() ,则
,则![]() ,
,
当且仅当![]() ,即
,即![]() 时取到最大值。
时取到最大值。
答:当存款利率定为![]() 时,银行可获得最大收益。
时,银行可获得最大收益。
23.已知![]() 抛物线M的方程为
抛物线M的方程为![]()
(1)求抛物线M的准线![]() 的方程;
的方程;
(2)求证:对任意![]() ,经过两点
,经过两点![]() 的直线与一定圆C想切,并求出圆C的方程;
的直线与一定圆C想切,并求出圆C的方程;
(3)设AB为定圆C的任意一条被直线![]() 平分的弦,求证:所有这些弦所在的直线都与某一条抛物线有且仅有一个公共点。
平分的弦,求证:所有这些弦所在的直线都与某一条抛物线有且仅有一个公共点。
(1)解:抛物线M的准线![]() 的方程为
的方程为![]() ,即
,即![]() 。
。
(2)证明:∵![]() ,
,
∴经过两点![]() 的直线方程为
的直线方程为![]() ,
,
∵原点到这条直线的距离![]() , ∴定圆C的方程为
, ∴定圆C的方程为![]() 。
。
(3)证明:设AB与直线![]() 的交点为
的交点为![]() ,则
,则![]() ,AB的方程为
,AB的方程为![]() ,
,
由题意设抛物线方程为![]() ,把
,把![]() 代入AB的方程,得
代入AB的方程,得
![]() ,由
,由![]() ,得
,得![]() ,
,
即所有这些弦所在的直线都与抛物线![]() 有且仅有一个公共点。
有且仅有一个公共点。
24.已知函数![]() 且
且![]()
(1)求![]() 的单调区间;
的单调区间;
(2)若函数![]() 与函数
与函数![]() 在
在![]() 时有相同的值域,求
时有相同的值域,求![]() 的值;
的值;
(3)设![]() ,函数
,函数![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
解:(1)![]() ,
,
易得![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() 。
。
(2)∵![]() 在
在![]() 上单调递减,∴其值域为
上单调递减,∴其值域为![]() ,即
,即![]() ,
,![]() 。
。
∵![]() 为最大值,∴最小值只能为
为最大值,∴最小值只能为![]() 或
或![]() ,
,
若![]()
![]() ;若
;若![]()
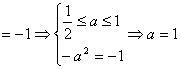 。综上得
。综上得![]() 。
。
(3)设![]() 的值域为
的值域为![]() ,由题意知,
,由题意知,![]()
![]()
![]() 。以下先证
。以下先证![]() 的单调性:设
的单调性:设![]() ,
,
∵![]() ,
,
(![]()
![]() ,
,![]() ), ∴
), ∴![]() 在
在![]() 上单调递减。
上单调递减。
∴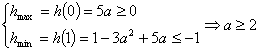 , ∴
, ∴![]() 的取值范围是
的取值范围是![]() 。
。